Исследование собственно-случайной и механической выборок
Обозначения
| Генеральная совокупность | Выборочная совокупность | |
| Среднее значение | 
| 
|
| Объем совокупности (число элементов в совокупности) | 
| 
|
| Доля признака | 
| 
|
| При изучении генерального среднего вычисляем:
|  , 
|
| При изучении генеральной доли вычисляем:
|  ,  ,
где m - число элементов в выборке, обладающих признаком
|
| Повторная выборка | Бесповторная выборка | |||
Средняя ошибка выборки, 
| для среднего
| 
| 
| |
| для доли
| 
| 
| ||
Предельная ошибка выборки, 
| 
| |||
Необходимый объем выборки, 
| для среднего
| 
| 
| |
| для доли
| 
| 
| ||
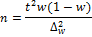
| Доверительный интервал | для ген.среднего
| 
| ||
| для ген. доли признака
| 
|
| t | 1,96 | |||
| P(t) | 0,693 | 0,95 | 0,954 | 0,997 |
При поиске 
или для доли признака в случае отсутствия 
можно использовать 
.
Занятие №3: Типовые задачи для решения в аудитории по теме “Выборочное наблюдение”.
№ 3.1. Из общей численности рабочих (5000 чел.) в порядке собственно-случайного бесповторного отбора для изучения времени простоев в течение рабочего дня было взято 500 человек. Получены следующие результаты:
| Группы рабочих по времени простоев, мин | До 10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | Свыше 60 |
| Число рабочих, чел. |
Определить: а) выборочную среднюю арифметическую времени простоя одного рабочего, ; б) среднюю ошибку выборочной средней, 
; в) предельную ошибку выборочной средней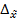 
с вероятностью 0,954; г) определите пределы, в которых находится генеральное значение среднего времени простоя одного рабочего с вероятностью 0,954; д) сколько человек необходимо отобрать для исследования времени простоев в течение рабочего дня, чтобы с вероятностью 0,95 утверждать, что предельная ошибка выборки 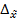не превысит 1,2.
|
|
№ 3.2. В рамках задачи №3.1 определить: а) выборочное значение доли рабочих , у которых время простоя выше 40 мин; б) среднюю ошибку выборочной доли, 
; в) предельную ошибку выборочной доли с вероятностью 0,997; г) интервал, в который с вероятностью 0,997 попадает генеральное значение доли рабочих, у которых время простоя выше 40 мин; д) сколько человек необходимо отобрать для исследования доли рабочих, у которых время простоя выше 40 мин, чтобы с вероятностью 0,954 утверждать, что предельная ошибка выборки не превысит 0,05.
№3.3. Определить минимальное число покупателей супермаркета, которое необходимо охватить в процессе выборочного наблюдения (собственно-случайная бесповторная выборка), чтобы с вероятностью 0,997 определить границы среднего размера покупки c предельной ошибкой 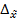не более 15 руб. Дисперсия размера покупок составила 7500.
Типовые задачи для решения дома по теме “Выборочное наблюдение”.
№ 3.4. Методом случайной повторной выборки было взято 500 шт. деталей для проверки веса. В результате при среднем квадратическом отклонении 
г. установлен средний вес детали 40 г. С вероятностью 0,954 определите пределы, в которых находится средний вес деталей генеральной совокупности.
№ 3.5. При разработке материалов учета характеристик городского населения методом случайного бесповторного отбора было установлено, что в городе 30% жителей старше 60 лет. Из общей численности населения (400 тыс. чел.) было отобрано 40 тыс. человек. С вероятностью 0,954 определите пределы, в которых находится доля жителей города в возрасте старше 60 лет.
|
|
№ 3.6. Определите, сколько семей необходимо охватить методом случайной бесповторной выборки для определения доли семей , не имеющих детей, с вероятностью 0,954 и предельной ошибкой не более 2%. Известно, что в регионе проживают 600 тыс. семей, а дисперсия признака составляет 0,19.
Ответы:
3.4. 
3.5. 
3.6. 1895 семей