Задачей регрессионного анализа является определение формы и параметров уравнений регрессии, характеризующих зависимость между случайными признаками, а также оценка значимости и доверительных границ этих параметров. Для двух случайных величин X и Y равенство вида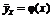 
называется уравнением регрессии. Функции 
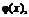как правило, линейны по оцениваемым параметрам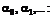 
, 
, 
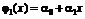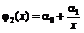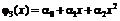и т.д.,
хотя относительно аргумента х могут быть и нелинейными.
Выборочные оценки параметров a1, a2, … могут быть получены методом наименьших квадратов.
Пусть известны результаты п наблюдений над системой случайных величин (X, Y):
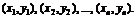
Параметры линейной функции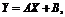 
характеризующей связь между X и Y, определяются из системы нормальных уравнений:
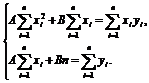
После деления каждого уравнения на п система приобретает вид
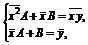
откуда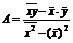 
= 
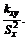
Полученное отношение называется выборочным коэффициентом регрессии Y на X и обозначается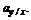 
Тогда линейное уравнение регрессии Y на X будет иметь следующий вид:
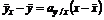, или 
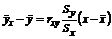, (13.1)
где rxy – выборочный коэффициент линейной корреляции.
Если результирующим признаком является Х, то выборочное уравнение регрессии X на Y запишется так:
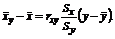(13.2)
Проверить значимость выборочных оценок a 0 и a 1 - значит установить, достаточна ли их величина для статистически обоснованного вывода о том, что параметры a0 и a1 уравнения регрессии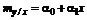 
отличны от нуля. С этой целью высказывают нулевую гипотезу H 0: a = 0. Рассматривается случайная величина
,
где a - выборочная оценка параметра a, Sa - ее среднее квадратичное отклонение. Для a 0 и a 1 отклонение Sa вычисляется по формулам:
,
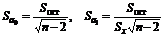где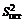 
- выборочная оценка остаточной дисперсии 
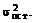Это среднее значение межгрупповых дисперсий, и оно является той частью общей дисперсии 
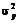результативного признака, которая обусловлена влиянием только случайных факторов.
Случайная величина T имеет распределение Стьюдента с n = n - 2 степенями свободы. Для заданного уровня значимости b и числа степеней свободы n по табл. 5 Приложений можно найти критическое значение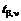 
. Если 
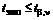, нулевая гипотеза принимается. Если же 
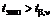, то гипотезу H 0 отвергают, считая параметр уравнения регрессии значимым.
Доверительный интервал для значимых параметров находят из условия
: 
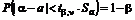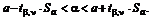
Для случаев, когда зависимость между случайными признаками X и Y нелинейна по переменным, оценка параметров уравнений регрессии осуществляется тем же методом наименьших квадратов. Простейшие нелинейные модели, которые могут быть использованы, таковы:
; 
; 
;
.
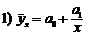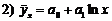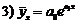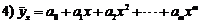Первые три формы связи легко линеаризуются заменой переменных величин:
в первом уравнении достаточно положить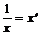 
, и уравнение становится линейным, 
;
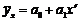во втором -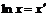 
, после чего 
;
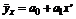в третьем следует сначала прологарифмировать обе части: 
, затем обозначить 
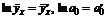и получить 
.
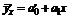13.1. В условиях задачи 12.1 требуется: а) найти условные средние случайных признаков; б) построить эмпирические линии регрессии; в) составить уравнения теоретических линий прямой регрессии и построить их; г) оценить значимость параметров полученных уравнений при уровне значимости b = 0,05; д) найти интервальную оценку для параметров уравнений при доверительной вероятности a = 0,95.
¢ Рассмотрим корреляционную табл. 12.2 из задачи 12.1. Вычислив условные средние признаков X и Y, заполним ими еще одну строку и столбец (табл. 13.1).
Таблица 13.1
 Y
X
| 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 |
|
|
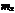
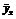
| 2,06 | ||||||||||
| 2,50 | ||||||||||
| 3,85 | ||||||||||
| 4,83 | ||||||||||
| 5,72 | ||||||||||
| 5,85 | ||||||||||
| 8,36 | ||||||||||
| ||||||||||
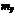
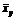
| 22,14 | 31,47 | 42,50 | 48,33 | 52,58 | 52,62 | 57,22 | 66,82 |
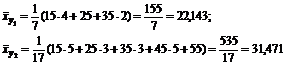
и т. д.,
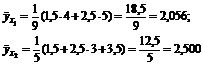
и т. д.
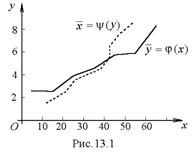
Построим эмпирические линии регрессии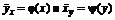 
(рис. 13.1).
Как видно, связь между признаками можно описать линейной зависимостью
|
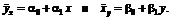
Найдем точечные оценки параметров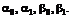 
Для этого воспользуемся уравнениям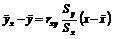и
и
.
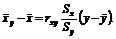Используя результаты задачи 12.1, получим
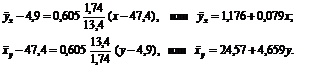
Итак,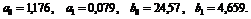 
Для оценки значимости этих параметров найдем сначала остаточные дисперсии составляющих системы, т.е. средние значения внутригрупповых дисперсий признаков X и Y.
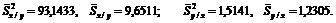
Затем вычислим средние квадратичные отклонения самих параметров:
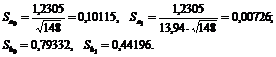
Далее находим эмпирические значения t -критерия Стьюдента по формуле
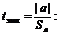
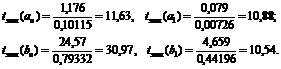
При заданном уровне значимости b = 0,05 и числе степеней свободы n = 148 из таблицы t -распределения Стьюдента (табл. 5 Приложений) находим критическое значение критерия: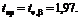 
Как видно, эмпирические значения критериев всех параметров уравнений регрессии значительно превышают критическое значение. Следовательно, значения параметров можно считать значимыми.
Находим интервальные оценки параметров уравнений:
1,176 – 1,97 × 0,10115 < a0 < 1,176 + 1,97 × 0,10115 Þ 0,977 < a0 < 1,375;
0,079 – 1,97 × 0,00726 < a1 < 0,079 – 1,97 × 0,00726 Þ 0,056 < a1 < 0,093;
24,57 – 1,97 × 0,79332 < b0 < 24,57 + 1,97 × 0,79332 Þ 23,01 < b0 < 26,13;
4,659 – 1,97 × 0,44196 < b1 < 4,659 + 1,97 × 0,44196 Þ 3,79 < b1 < 5,53. £
В задачах 13.2 – 13.5 по данным корреляционных таблиц вы-полнить линейный регрессионный анализ для случайных признаков X и Y.
13.2.
| Y | ||||||||||||||||
| Х | 15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 | 75-85 | |||||||||
| 200 – 300 | ||||||||||||||||
| 300 – 400 | ||||||||||||||||
| 400 – 500 | ||||||||||||||||
| 500 – 600 | ||||||||||||||||
| 600 – 700 | ||||||||||||||||
| 700 – 800 | ||||||||||||||||
| 800 – 900 | ||||||||||||||||
13.3.
| X | Y | ||||||
13.4.
| X | Y | |||||
| 15-20 | 20-25 | 25-30 | 30-35 | 35-40 | 40-45 | |
| 210 – 220 | ||||||
| 220 – 230 | ||||||
| 230 – 240 | ||||||
| 240 – 250 | ||||||
| 250 – 260 | ||||||
| 260 – 270 |
13.5.
| X | Y | ||||||
| 0,02 | 0,06 | 0,10 | 0,14 | 0,18 | 0,22 | 0,26 | |
| 10 – 20 | |||||||
| 20 – 30 | |||||||
| 30 – 40 | |||||||
| 40 – 50 | |||||||
| 50 – 60 | |||||||
| 60 – 70 | |||||||
| 70 – 80 |
13.6. Измерение температуры корпуса работающего агрегата, произведенное с интервалом в 5 минут, дало следующие резуль-таты:
| t, мин | |||||
| T, ° C | 59,3 | 59,8 | 60,1 | 64,9 | 70,2 |
Считая, что зависимость между этими переменными имеет вид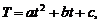 
найти методом наименьших квадратов оценки параметров a, b и c.
¢ Предварительно преобразуем исходные данные по формулам
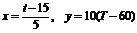
и вычислим оценки параметров линейной модели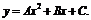 
В данном случае система нормальных уравнений выглядит следующим образом:
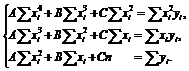
Для вычисления коэффициентов системы составим таблицу (13.2).
Таблица 13.2
| t | T | x | y | xy | x2y | x 2 | x 3 | x 4 |
| 59,3 59,8 60,1 64,9 70,2 | -2 -1 | -7 -2 | -28 -2 | -8 -1 | ||||
|
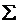
Составляем систему нормальных уравнений:
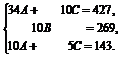
Решив систему, получим А » 10,07, В = 26,9, С » 8,457. Таким образом, зависимость между x и y имеет вид
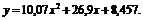
Переходя к исходным переменным, получим:
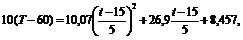или окончательно
. £
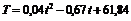В задачах 13.7 – 13.9 найти оценки параметров уравнения регрессии, считая, что зависимость между переменными имеет вид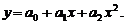 
13.7.
| х | ||||||
| у | -1 | -0,5 | 1,5 | 4,5 | 8,5 |
13.8.
| х | 0,07 | 0,31 | 0,61 | 0,99 | 1,29 | 1,78 | 2,09 |
| у | 1,34 | 1,08 | 0,94 | 1,06 | 1,25 | 2,01 | 2,60 |
13.9.
| х | |||||||
| у | 3,94 | 4,60 | 5,67 | 6,93 | 8,25 | 7,73 | 10,55 |
В задачах 13.10 – 13.11 найти оценки параметров уравнения регрессии, считая, что зависимость между переменными имеет вид
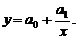
13.10.
| х | ||||
| у | 5,25 | 3,50 | 3,25 |
13.11.
| х | 5,67 | 4,45 | 3,84 | 3,74 | 3,73 | 2,18 |
| у | 6,5 | 6,8 | 7,0 | 7,6 | 8,8 | 11,9 |
13.12. Найти оценки для параметров модели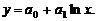 
| х | 0,3 | 0,6 | 0,9 | 1,2 | 1,5 | 1,8 | 2,1 |
| у | 4,39 | 4,75 | 4,98 | 5,11 | 5,12 | 5,18 | 5,28 |
| х | 2,4 | 2,7 | 3,0 | 3,3 | 3,6 | 3,9 | 4,2 |
| у | 5,36 | 5,45 | 5,52 | 5,53 | 5,57 | 5,63 | 5,64 |
13.13. Найти оценки для параметров модели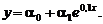 
| х | 1,5 | 2,5 | 3,5 | ||||
| у | 4,11 | 4,16 | 4,23 | 4,29 | 4,36 | 4,42 | 4,53 |
| х | 4,5 | 5,5 | 6,5 | |||
| у | 4,57 | 4,63 | 4,75 | 4,87 | 4,88 | 5,01 |