Какая из функций является линейной?

Вариант 7

I часть ( 5 баллов)

Задания 1-5 имеют четыре варианта ответа, из которых только один верный. Выберите верный ответ. Верный ответ каждого задания оценивается одним баллом.

1. Решите неравенство

А) (-∞; 6) (8;+∞); Б) [6;8];

B) (-∞; 6] [8;+∞); Г) (6;8).

2. Какая из функций является линейной?

А) y = Б) y = ;

B) y = x²+1; Г) y = 5.

3.При каких значениях х выражение имеет смысл?

A) x 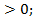Б) х

В) х Г) х

4. Найдите произведение корней уравнений и 5х – 1 = 4.

А)-5; Б) 5;

В) 3; Г) -3.

5. Упростить выражение + :

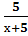А) 1; Б) ; В) Г) 0.

II часть (4 балла)

Решение заданий 6-7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

Найдите четыре числа, которые образуют геометрическую прогрессию, если первый член больше третьего на 6, а второй меньше четвертого на 3.

7. Постройте график функции и найдите координаты точек пересечения графиков у= 2х − 2 и у = −4.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

За 5 часов движения по течению и 3 часа против течения пароход прошел 244 км. Найдите собственную скорость парохода и скорость течения реки, если за два часа по течению и 30 минут против течения пароход прошел 78 км.

Вариант 8

I часть ( 5 баллов)

Задания 1-5 имеют четыре варианта ответа, из которых только один верный. Выберите верный ответ. Верный ответ каждого задания оценивается одним баллом.

1. При каких значениях х выражение имеет смысл?

А) 4; Б) 3; В) -1; Д) 10.

Какая из функций является линейной?

А) у= -3х+1; Б) у= х²;

В) у= Г) у=

3. Найдите три первых члена последовательности, которая задана формулой а_n = 3n+1, где n

A) 5;7;10; Б) 4;6;10;

В) 4;7;10; Г) 5;8;10.

4. Найдите произведение корней уравнений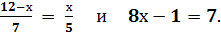

А) 1; Б) -1; В) 5; Г) -5.

5. Упростить выражение ―

А) 0; Б) ;

В) Г) 1.

II часть (4 балла)

Решение заданий 6-7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

6. Решите систему уравнений

7. Постройте график функции и найдите координаты точек пересечения графиков у = − 2х+4 и у = 2х.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

Если из одного пункта в одном направлении отправятся велосипедист и мотоциклист, то через два часа расстояние между ними будет 14 км. Если же они отправятся одновременно в противоположных направлениях, то через 3 часа расстояние между ними будет 174 км. Найдите скорость каждого из них.

Вариант 9

I часть ( 5 баллов)

Задания 1-5 имеют четыре варианта ответа, из которых только один верный. Выберите верный ответ. Верный ответ каждого задания оценивается одним баллом.

1. При каких значениях х выражение имеет смысл?

А) 4; Б) - 3;

В) 2; Д) -1.

Какая из функций является линейной?

А) у = х²; Б) у = - ;

В) у = 2х; Г) у = -4+х².

Напишите четыре первых члена последовательности нечетных натуральных чисел.

А) 1;3;5;7; Б) 3;5;7;9;

В) 1;5;9;13; Г) -1;-3;-5;-7.

4. Вычислите дискриминант уравнения 2у²+3у+1=0.

А) 11; Б) 17;

В) -5; Г) 1.

5. Упростить выражение :

А) 2(х + 5); Б) 2(х - 5);

В) 4(х + 5); Г) х − 10.

II часть (4 балла)

Решение заданий 6-7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами

6. Решите систему уравнений

7. Постройте график функции и найдите координаты точек пересечения графиков у =−- и у = − 2х.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

За 5 часов движения по течению и 2 часа против течения пароход проходит 181 км, а за два часа по течению и 3 часа против течения – проходит 123 км. Найдите собственную скорость парохода и скорость течения реки.

Вариант 10

I часть ( 5 баллов)

Задания 1-5 имеют четыре варианта ответа, из которых только один верный. Выберите верный ответ. Верный ответ каждого задания оценивается одним баллом.

1. Какое число является решением неравенства 16 ²

А) 4; Б) 3; В) 9; Г) 10.

Какая из функций является линейной?

А) y = Б) y = 6

B) y = ; Г) y =

3. Напишите три первых члена последовательности, заданной формулой a_n =5n , где n

А) 4;8;13; Б) 3;8;13;

В) 5;8;6; Г) 3;9;13.

4. Вычислите дискриминант уравнения 2у²+5у+2 =0.

А) 41; Б) 9;

В) -11; Г) 21.

5. Упростить выражение .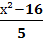

А) 5(х – 4); Б) 5(х+4); В) -5(х-4); Г) 5.

II часть (4 балла)

Решение заданий 6-7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами

6. Решите систему уравнений

7. Постройте график функции и найдите координаты точек пересечения графиков у = и у = 3х.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

Из пункта А в пункт Б, расстояние между которыми 5 км, вышел пешеход, а через 30 минут следом за ним выехал велосипедист, скорость которого на 10 км/ч больше чем скорость пешехода. В пункт Б велосипедист приехал на 10 минут раньше пешехода. Найдите скорость велосипедиста и пешехода.

Вариант 11

I часть ( 5 баллов)

Задания 1-5 имеют четыре варианта ответа, из которых только один верный. Выберите верный ответ. Верный ответ каждого задания оценивается одним баллом.

1. При каких х определена данная функция у= .

А) х ; Б) х ; В) х 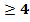; Г) Х

2. Решите неравенство (х . Выберите правильный ответ.

А) ( Б) [ 2; 3 ];

B) (2;3); Г) [ -2; 3 ].

3. Напишите четыре первых члена последовательности, заданной формулой х_n= 2n , где n

A) 1;4;7;10; Б)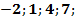

В) 4;7;10;13; Г) 1;3;5;7.

4. Вычислите дискриминант уравнения х² – 6х + 5=0.

А) 16; Б) 56;

В) -16; Г) 56.

5. Упростить выражение .

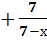А) ─ 1; Б) ; В) ; Г) 1.

II часть (4 балла)

Решение заданий 6-7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами

6. Решите систему уравнений

7. Постройте график функции у= х² − 2х −3. Найдите промежуток, на котором функция возрастает.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

8. Из пункта А в пункт Б, расстояние между которыми 10 км, выехал велосипедист, а через 30 минут следом за ним ― мотоциклист, скорость которого на 30 км/ч больше чем скорость велосипедиста. Найдите скорость велосипедиста и мотоциклиста, если в пункт Б мотоциклист приехал на 15 минут раньше велосипедиста.

Вариант 12

I часть ( 5 баллов)

Задания 1-5 имеют четыре варианта ответа, из которых только один верный. Выберите верный ответ. Верный ответ каждого задания оценивается одним баллом.

1. При каких х определена данная функция у= .

А) х ; Б) х ; В) х ; Г) х

2. Решите неравенство (х . Выберите правильный ответ.

А) ( 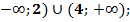Б) [ 2; 4 ];

B) ( ; Г) (2; 4).

3. Найдите три первых члена последовательности, заданной формулой х_n =2n 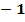, где n

А) - 1;1;3; Б) 3;5;7;

В) 1;3;5; Г) 1;5;9.

4. Вычислите дискриминант уравнения х² – 7х + 12 =0.

А) -1; Б) -97;

В) 1; Г) 97.

5. Упростить выражение .

А) 1; Б) ; В) ; Г) .

II часть (4 балла)

Решение заданий 6-7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами

6. Решите систему уравнений

7. Постройте график функции у= х² + 2х −3. Найдите промежуток, на котором функция убывает.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

Из двух городов, расстояние между которыми 900 км, отправляются навстречу друг другу два поезда и встречаются на середине пути. Определите скорость каждого поезда, если первый вышел на 1 час позже другого со скоростью большей на 5 км/ч, чем скорость другого поезда.