Лабораторная работа №5
Множественная линейная регрессия.
Понятие множественной линейной регрессии.
Множественная регрессия представляет собой уравнение связи с не-
сколькими независимыми переменными:
где у – зависимая переменная (результативный признак); х1,х2,…,хp – неза-
висимые переменные (факторы).
Основная цель множественной регрессии – построить модель с большим
числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
Постановка задачи множественной регрессии. По имеющимся данным
n наблюдений за совместным изменением p +1 переменной y и xj и {(yi, xj,i);
j =1,2,..., p; i =1,2,..., n } (табл. 3.1) необходимо определить аналитическую зависимость ŷ = f (x 1, x 2,..., xp), наилучшим образом описывающую данные наблюдений.
Как и в случае парной регрессии, построение уравнения множественной
регрессии осуществляется в два этапа:
– спецификация модели;
– оценка параметров выбранной модели.
Спецификация модели включает в себя решение двух задач:
– отбор p факторов xj, наиболее влияющих на величину y;
– выбор вида уравнения регрессии ŷ = f (x 1, x 2,..., xp);.
Отбор факторов при построении множественной регрессии
Включение в уравнение множественной регрессии того или иного набора
факторов связано, прежде всего, с представлением исследователя о природе
взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать требованиям:
1. Факторы не должны быть взаимно коррелированы и, тем более, нахо-
диться в точной функциональной связи. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель, и параметры уравнения регрессии оказываются неинтерпретируемыми.
2. Включаемые во множественную регрессию факторы должны сущест-
венно влиять на вариацию независимой переменной. Т. е. включаемые в модельфакторы должны быть статистически значимыми и существенно улучшать показатель качества модели (например, коэффициент детерминации R 2).
Отбор факторов производится на основе качественного теоретико-
экономического анализа и осуществляется в две стадии:
– на первой стадии факторы подбираются исходя из сущности проблемы;
– на второй стадии применяются формальные статистические критерии, на-
пример, значения t- статистики для соответствующих коэффициентов регрессии. Наличие высокой корреляции выявляется по значению линейного коэффициента корреляции rxix j.
Если выполняется условие
то факторные переменные xi, x j находятся в линейной зависимости между со-
бой, а сами переменные xi, x j называются явно коллинеарными.
Значения линейных коэффициентов корреляции rxix j для всевозможных
комбинаций переменные xi, x j составляют корреляционную матрицу { rxi x j }.
Для трех факторов матрица { rxix j } принимает вид:
В уравнение регрессии включается только один из коллинеарных факторов,
при этом предпочтение отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
Для преодоления сильной межфакторной корреляции используется ряд
подходов:
– исключение из модели одного или нескольких факторов;
– преобразование факторов, при котором уменьшается корреляция между ними;
– переход к совмещенным уравнениям регрессии, т. е. к уравнениям, кото-
рые отражают не только влияние факторов, но и их взаимодействие.
После исключения коллинеарных факторов осуществляется процедура от-
бора факторов, наиболее влияющих на изменение результативного признака
(факторов, включаемых в регрессию). Наиболее широкое применение получили:
метод исключения;
метод включения.
В уравнении регрессии включаются только значимые факторы, что прове-
ряется с помощью критерия Стьюдента.
При отборе факторов рекомендуется пользоваться
следующим правилом: число включаемых факторов должно быть в 6–7 раз
меньше объема совокупности, по которой строится регрессия.
Выбор формы уравнения регрессии:
В уравнении линейной множественной регрессии
параметры bi при хi называются коэффициентами «чистой» регрессии и интер
претируется следующим образом. Параметры bi характеризуют среднее изме-
нение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.
Оценка параметров уравнения множественной регрессии
Для оценки параметров уравнения множественной регрессии применяют
метод наименьших квадратов (МНК). Для линейных уравнений регрессии
строится система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии. В случае линейной множественной регрессии система нормальных уравнений имеет следующий вид:
Частные уравнения регрессии
Уравнение линейной множественной регрессии позволяет построить,
частные уравнения регрессии, показывающие зависимость результативного признака от отдельного фактора, при исключении влияния остальных факторов, входящих в уравнение множественной регрессии.
Частные уравнения регрессии получаются из уравнения множественной
регрессии с помощью замены всех факторов, кроме одного на их средние
значения.
Уравнения можно представить в виде
где
Множественная корреляция
Коэффициент множественной корреляции характеризует тесноту связи
рассматриваемого набора факторов с исследуемым признаком, или, оценивает тесноту совместного влияния факторов на результат и вычисля-
ется по формуле:
где n – количество наблюдений; xi, yi – данные наблюдений;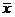 
, 
средние
значения переменных x и y; 
расчетные значения переменной y, вычисленные по уравнению множественной регрессии, т. е. ŷ = f (x 1, x 2, …, x p). Коэффициент множественной корреляции изменяется от 0 до 1. Чем ближнего значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина коэффициента множественной корреляции больше или равна максимальному парному коэффициенту корреляции.
При правильном включении факторов в регрессионный анализ величина
индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Квадрат коэффициента множественной корреляции называется коэффициентом детерминации и обозначается 
. Величина коэффициента детерминации используется для оценки качества регрессионной модели. Чем его величина больше, тем лучше данная модель согласуется с данными наблюдений. Низкое значение коэффициента (индекса) множественной корреляции означает, что либо в регрессионную модель не включены существенные факторы, либо рассматриваемая форма связи не отражает реальные соотношения между
переменными, включенными в модель. В этом случае требуются дальнейшие
исследования по улучшению качества модели и увеличению ее практической
значимости.
Оценка качества результатов моделирования
Статистическая значимость уравнения множественной регрессии в целом
оценивается с помощью F -критерия Фишера. Статистическая значимость коэффициентов уравнения множественной регрессии в целом оценивается с помощью t -критерия Стьюдента.
Проверка остатков регрессии на гомоскедастичность
Для того чтобы МНК давал надежные оценки параметров линейной рег-
рессии, требуется чтобы дисперсии остатков модели ε.
для каждого наблюдения были одинаковыми. Остатки, обладающие таким свойством, называются гомоскедастичными, а не обладающие – гетероскедастичными. При нарушении гомоскедастичности имеем неравенства
Для оценки гетероскедастичности можно использовать метод Гольдфель-
да–Квандта, который проверяет наличие зависимости остатков ε от одной из
факторных переменных хi. Алгоритм применения теста Гольдфельда–Квандта состоит из следующих шагов:
1) исходные данные наблюдений упорядочиваются по мере возрастания
выбранной переменной хi;
2) выделяются первые nо и последние nо наблюдений и исключаются из
рассмотрения С = n– 2 nо центральных наблюдений. При этом должно выпол-
няться условие n0 > р, где p – число оцениваемых параметров;
3) для каждой из групп наблюдений оцениваются уравнения регрессии ос-
татков ε по значимым факторам
4) для каждого уравнения определяются остаточные суммы квадратов (S 1)
и (S 2) остатков ui и находится их отношение: R = max(S 2, S 1) / min(S 2, S 1).
Если выполняется условие
где Fтабл представляет собой табличное значение F -критерия Фишера при уровне значимости α и числе степенях свободы k 1 = n0 – р, k 2 = n0 – р, то предпосылка о равенстве дисперсий остаточных величин отвергается с уровнем значимости α.
Чем больше величина R превышает табличное значение критерия Fтабл, тем
более нарушена предпосылка о равенстве дисперсий остаточных величин.
Рекомендовано для случая одного фактора n =20 принимать С =4, при n =30 принимать С =8, при n =60 принимать С =16.
Контрольные вопросы
1. Что понимается под множественной регрессией?
2. Какие задачи решаются при построении уравнения регрессии?
3. Какие задачи решаются при спецификации модели?
4. Какие требования предъявляются к факторам, включаемым в уравнение регрессии?
5. Что понимается под коллинеарностью факторов?
6. Как проверяется наличие коллинеарности?
7. Какие подходы применяются для преодоления межфакторной корреляции?
8. Какие функции чаще используются для построения уравнения множествен
ной регрессии?
9. По какой формуле вычисляется индекс множественной корреляции?
10. Как вычисляются индекс множественной детерминации?
11. Что означает низкое значение коэффициента множественной корреляции?
12. Как проверяется значимость уравнения регрессии и отдельных коэффициентов?
13. Как строятся частные уравнения регрессии?
14. Как вычисляются средние частные коэффициенты эластичности?
15. Что понимается под гомоскедастичностью ряда остатков?
16. Как проверяется гипотеза о гомоскедастичности ряда остатков?
Лабораторная работа №5. Множественный регрессионный анализ:
построение модели в виде уравнения множественной регрессии с учетом
только значимых факторов и проверка ее качества
Задание. На основании данных:
1) Проверить факторы на наличие коллинеарности. Отобрать неколлине-
арные факторы.
2) Построить уравнение линейной множественной регрессии.
3) Определить значения коэффициента множественной корреляции и ко-
эффициента детерминации.
4) Проверить значимость уравнения при заданном уровне значимости.
5) Проверить значимость коэффициентов уравнения при заданном уровне
значимости.
6) Построить уравнение линейной множественной регрессии с учетом
только значимых факторов.
7) Проверить гипотезу о гомоскедастичности ряда остатков с уровнем зна-
чимости α = 0,05.
8) Построить частные уравнения регрессии.
9) Определить средние частные коэффициенты эластичности.
Указания к решению. При выполнении лабораторной работы использовать возможности надстройки «Анализ данных» табличного процессора MS Excel (для расчета корреляционной матрицы, нахождения уравнений регрессии, нахождения коэффициентов координации и др.), либо
Пример выполнения лабораторной работы №5
Исходные данные:
данные наблюдений переменных y и x 1, x 2, x 3 даны в таблице;
уровень значимости α = 0,05.
Исходные данные для примера выполнения лабораторной работы №5
1) Проверка факторов на наличие коллинеарности. Отбор некол-
линеарных факторов.
Построим корреляционную матрицу, используя функцию «Сервис.Анализ
данных.Корреляция» табличного процессора MS Excel.
Корреляционная матрица
Из матрицы следует, что
,
следовательно, коллинеарность между факторами отсутствует и нет основания исключать какой-либо фактор из рассмотрения, регрессия y по строится по факторам x 1, x 2 и x 3.
2) Построение уравнения линейной множественной регрессии.
Для построения уравнения линейной регрессии используем функцию
«Сервис.Анализ данных.Регрессия» табличного процессора MS Excel:
1) вызов функции осуществляется через пункты меню: <Сервис> – <Ана-
лиз данных> – <Регрессия>;
2) указываются ячейки, содержащие исходные значения переменных y и xi;
3) если отсутствует свободный член в уравнении регрессии – установить
флажок «Константа–ноль»;
4) указать место, где будут представлены результаты работы функции (вы-
ходной интервал на данном рабочем листе, новый рабочий лист, новая рабочая книга);
5) искомые значения коэффициентов линейного уравнения регрессии (a, bi)
берутся из столбца «Коэффициенты» таблицы результатов регрессии.
Окно ввода параметров регрессии MS Excel
Результаты работы функции приведены в таблицах
Результаты корреляционного анализа.
Результаты дисперсионного анализа
Результаты регрессионного анализа
Из таблицы следует, что уравнение регрессии имеет вид
y = –99,816 + 0,154·x1 + 4,459·x2 + 0,324·x3.
3) Определение значений коэффициента множественной корреляции R и
коэффициента детерминации .
Из таблицы R = 0,748; R2 = 0,560.
4) Проверка значимости уравнения регрессии.
Применим F -критерий Фишера. Вычислим фактическое значение критерия
Это же значение Fфакт можно было взять из таблицы
Определим критическое значение критерия Fкрит F -критерия Фишера, используя функцию MS Excel «FРАСПОБР()»:
уровень значимости α = 0,05;
число степеней свободы k 1 = m = 3; k 2 = n - m - 1 = 30 - 3 - 1 = 26;
Fкрит = FРАСПОБР(0,05; 3; 26) = 2,98.
Так как 
= 11,01 > Fкрит = 2,28, то делаем вывод о значимости построенного уравнения регрессии.
Из таблицы следует, что уровень значимости уравнения регрессии
α = 
, т. е. заведомо ниже требуемого уровня α = 0,05, т. е. уравнение
значимо и при более низком уровне значимости.
5) Проверка значимости коэффициентов уравнения регрессии.
Применим t- критерий Стьюдента. Из таблицы следует, что уровни зна-
чимости коэффициентов уравнения регрессии имеют значения:
α a = 0,050; α b 1 = 0,058; α b 2 = 0,005; α b 3 = 0,023.
Таким образом, оценки параметров a, b 2, b 3 значимы при уровне значимо-
сти α = 0,05, а значение b 1 не значимо при уровне значимости α = 0,05.
6) Построение уравнения линейной множественной регрессии с учетом
только значимых факторов.
Значимыми факторами являются x 2, x 3.
Для построения уравнения линейной регрессии используем функцию
«Сервис.Анализ данных.Регрессия» табличного процессора MS Excel.Задав соответствующие диапазоны данных в окне ввода параметров регрессии. Множественный коэффициент корреляции R = 0,702,Коэффициент детерминации R2 = 0,493,
= 13,12,
уровень значимости уравнения регрессии α = 0,01.
Результаты регрессионного анализа.
Из таблицы следует, что уравнение регрессии имеет вид
y = 89,520 + 4,082· x 2 + 0,361· x 3.
7) Построение частных уравнений регрессии
на основании уравнения
y = 89,520 + 4,082· x 2 + 0,361· x 3.
Определим средние значения переменных используя функции СРЗНАЧ()
табличного процессора MS Excel x 2, x 3, y
x 2 = СРЗНАЧ() = 37,70; x 3 = 168,27; y = 125,17.
Вычислим свободные члены частных уравнений регрессии (3.7)
Частные уравнения регрессии
y y, x 2 = –28,77 + 4,082· x 2,
y y, x 3 = 64,37 + 0,361· x 3.
Результаты.
1) Проверка факторов на наличие коллинеарности показала, что коллине-
арность между факторами отсутствует.
2) Уравнение линейной множественной регрессии
y = –99,816 + 0,154·x1 + 4,459·x2 + 0,324·x3.
3) Значения коэффициента множественной корреляции R и коэффициента
детерминации R2
R = 0,748; R2 = 0,560.
4) Проверка значимости уравнения регрессии.
y = –99,816 + 0,154·x1 + 4,459·x2 + 0,324·x3.
Построенное уравнение регрессии значимо при уровне значимости α = 0,05.
5) Проверка значимости коэффициентов уравнения регрессии.
Оценки параметров a, b 2, b 3 значимы при уровне значимости α = 0,05, а
значение b 1 не значимо при уровне значимости α = 0,05.
6) Построение уравнения линейной множественной регрессии с учетом
только значимых факторов.
Уравнение регрессии имеет вид
y = 89,520 + 4,082· x 2 + 0,361· x 3.
7) Частные уравнения регрессии
y y, x 2 = –28,77 + 4,082· x 2,
y y, x 3 = 64,37 + 0,361· x 3.