Имеются следующие данные по 21 региону.
| № | Y | X1 | X2 | X3 |
| 55,0 | 27,0 | 63,0 | ||
| 16,0 | 57,0 | 50,0 | ||
| 50,0 | 58,0 | 47,0 | ||
| 49,0 | 53,0 | 50,0 | ||
| 58,0 | 36,0 | 14,0 | ||
| 59,0 | 53,0 | 64,0 | ||
| 38,0 | 16,0 | 54,0 | ||
| 49,0 | 38,0 | 66,0 | ||
| 22,0 | 34,0 | 36,0 | ||
| 43,0 | 19,0 | 43,0 | ||
| 39,0 | 23,0 | 50,0 | ||
| 31,0 | 24,0 | 35,0 | ||
| 57,0 | 29,0 | 12,0 | ||
| 23,0 | 38,0 | 62,0 | ||
| 49,0 | 44,0 | 29,0 | ||
| 31,0 | 53,0 | 16,0 | ||
| 14,0 | 35,0 | 42,0 | ||
| 68,0 | 18,0 | 48,0 | ||
| 39,0 | 50,0 | 59,0 | ||
| 14,0 | 60,0 | 23,0 | ||
| 58,0 | 60,0 | 25,0 |
Задание:
1. Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов (2 способами: матричным и с помощью функции Excel).
2. Оцените показатели вариации каждого признака и сделайте вывод о возможностях применения МНК для их изучения.
3. Дайте сравнительную оценку силы связи факторов с результатом с помощью средних (общих) коэффициентов эластичности.
4. Оцените статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о значимости уравнения и показателей тесноты связи проверьте с помощью F- критерия.
5. Оцените качество уравнения через среднюю ошибку аппроксимации.
6. Рассчитайте коэффициент детерминации и скорректированный коэффициент детерминации.
7. Рассчитайте матрицы парных и частных коэффициентов корреляции и на их основе сделайте выводы по модели.
8. Отберите информативные факторы в модель. Постройте модель только с информативными факторами и оцените ее параметры.
9. Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80 % от их максимальных значений.
10. Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 5 % (
).
11. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
1. Рассчитаем параметры линейного уравнения множественной регрессии с полным перечнем факторов:
А) матричным способом:
, где 
- матрица, составленная из факторов регрессии, включая столбец 1, 
- матрица-столбец, составленная из результирующего фактора.
| х | |||
| хт*х | |||
| обр.хт*х | |||
| 1,23756 | -0,00918 | -0,01168 | -0,00838 |
| -0,00918 | 0,000192 | 3,32E-05 | -4E-08 |
| -0,01168 | 3,32E-05 | 0,000235 | 2,61E-05 |
| -0,00838 | -4E-08 | 2,61E-05 | 0,000174 |
| бетта |
| 629,1271 |
| -0,40261 |
| 1,39136 |
| -0,5974 |
Б) с помощью функции Excel «Регрессия»:
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0,396299 | |||||||
| R-квадрат | 0,157053 | |||||||
| Нормированный R-квадрат | 0,008298 | |||||||
| Стандартная ошибка | 65,50267 | |||||||
| Наблюдения | ||||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 13589,8 | 4529,934 | 1,055781 | 0,393688 | ||||
| Остаток | 72940,2 | 4290,6 | ||||||
| Итого | ||||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 629,1271 | 72,86889 | 8,633686 | 1,27E-07 | 475,3872 | 782,8671 | 475,3872 | 782,8671 |
| X1 | -0,40261 | 0,907325 | -0,44373 | 0,662833 | -2,3169 | 1,511681 | -2,3169 | 1,511681 |
| X2 | 1,39136 | 1,003219 | 1,386896 | 0,183391 | -0,72525 | 3,507967 | -0,72525 | 3,507967 |
| X3 | -0,5974 | 0,863823 | -0,69158 | 0,498538 | -2,41991 | 1,225103 | -2,41991 | 1,225103 |
Уравнение регрессии с полным перечнем факторов примет вид: 
2. Оценить показатели вариации каждого признака и сделать выводы о возможностях применения МНК для их изучения
, 
, 
, 
Для расчета составим вспомогательную таблицу:
| Y | X1 | X2 | X3 | ||||
| Среднее | Среднее | 41,04762 | Среднее | 39,28571 | Среднее | 42,28571 | |
| Стандартная ошибка | 14,35353 | Стандартная ошибка | 3,567363 | Стандартная ошибка | 3,253674 | Стандартная ошибка | 3,732191 |
| Медиана | Медиана | Медиана | Медиана | ||||
| Мода | #Н/Д | Мода | Мода | Мода | |||
| Стандартное отклонение | 65,77614 | Стандартное отклонение | 16,34771 | Стандартное отклонение | 14,91021 | Стандартное отклонение | 17,10305 |
| Дисперсия выборки | 4326,5 | Дисперсия выборки | 267,2476 | Дисперсия выборки | 222,3143 | Дисперсия выборки | 292,5143 |
| Эксцесс | -0,63225 | Эксцесс | -1,01202 | Эксцесс | -1,40699 | Эксцесс | -0,97895 |
| Асимметричность | -0,17918 | Асимметричность | -0,32932 | Асимметричность | -0,04594 | Асимметричность | -0,39567 |
| Интервал | Интервал | Интервал | Интервал | ||||
| Минимум | Минимум | Минимум | Минимум | ||||
| Максимум | Максимум | Максимум | Максимум | ||||
| Сумма | Сумма | Сумма | Сумма | ||||
| Счет | Счет | Счет | Счет |
, 
,
, 
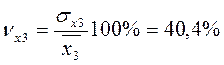
| Показатели вариации | Y | 10,24550397 | ||
| X1 | 39,82620742 | |||
| X2 | 37,95325529 | |||
| X3 | 40,4463997 |
Вывод: значения коэффициентов вариации для фактора у, невысокие (не превышают 33%), к ним можно применить МНК для оценки коэффициентов регрессии. А вот для фактора Х1, Х2, Х3 этот показатель завышен, совокупность неоднородная для анализа.