Министерство общего и профессионального образования РФ
Иркутский государственный технический университет
Учись решать задачи
Квантовая оптика
Часть 2. Давление света, Фотоэффект,
Эффект Комптона
Методические указания по курсу общей физики
Иркутск 1998
Учись решать задачи. Квантовая оптика. Часть 2: Давление света,
Фотоэффект, эффект Комптона. Методические указания по курсу общей физики. Составители: Шигорова Т.А., Липовченко Е.Л., Любушкин В.А. – Иркутск, 1998. –24 с.
В краткой форме содержит необходимый теоретический материал,
качественные и расчётные задачи. Задачи сопровождаются анализом их физи-
ческого содержания и подробным решением.
Предназначено в помощь студентам при их самостоятельной
работе по изучению раздела «Квантовая оптика ».
Рецензенты: канд. физ.-мат. наук Г.А. Кузьмина
канд. физ. –мат. наук Л.А. Сомина
Рекомендовано кафедрой физики ИрГТУ.
Indocti discant et ament meminisse periti
(Незнающие пусть научатся, а знающие вспомнят ещё раз)
I. Введение.
В данном разделе будут изложены краткие сведения о теории таких, сугубо квантовых, свойствах света, как давление света, фотоэффект и эффект Комптона. Объединение этих явлений в одну группу обусловлено тем, что все они объясняются упругим или неупругим рассеянием световых квантов частицами вещества (в основном, электронами). Действительно, давление света обусловлено частичным поглощением фотонов (неупругое рассеяние) и частичным их отражением (упругое рассеяние); фотоэффект вызван абсолютно неупругим рассеянием квантов, а эффект Комптона - это абсолютно упругое их рассеяние на свободных электронах. Элементарная теория этих явлений достаточно проста.
В соответствии с гипотезой световых квантов, свет испускается, поглощается и распространяется дискретными порциями - квантами, которые также называются фотонами. Энергия кванта света равна:
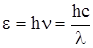 (1.1)
(1.1)
Согласно знаменитой формуле Эйнштейна любой материальный объект, имеющий массу, обладает в силу этого энергией
 (1.2)
(1.2)
Однако будет справедливо и обратное утверждение: любому объекту, обладающему энергией, можно приписать строго определенную массу. По формулам (1.2) и (1.1) можно рассчитать и массу фотона:
 (1.3)
(1.3)
Всякая движущаяся частица, обладающая массой, имеет и отличный от нуля импульс. Фотоны всегда движутся со скоростью света (с). Поэтому их импульс
 (1.4)
(1.4)
Эти предварительные сведения понадобятся нам в дальнейшем при рассмотрении явлений, в которых проявляются квантовые свойства света.
1. Давление света. Поскольку фотоны обладают импульсом, то падающий на произвольную поверхность свет, должен оказывать на нее давление. Этот факт легко понять, если вспомнить, что газы оказывают давление на стенки вмещающих их сосудов именно в результате передачи этим стенкам импульсов хаотически двигающихся молекул. С точки зрения квантовой теории давления света также обусловлено тем, что каждый фотон при соударении с поверхностью передает ей определенный импульс.
Пусть за единицу времени нормально к поверхности единичной площади падает N фотонов. При этом aN фотонов отразится, а (1-a)N фотонов поглотится (a - коэффициент отражения). Давление света на эту единичную поверхность будет равно импульсу, который ей передают N фотонов за 1с:
 (1.5)
(1.5)
Произведение Nhn есть энергетическая освещенность Ee данной поверхности, равная световой энергии, падающей на единицу поверхности за единицу времени, а Е е / с= w - объемная плотность энергии излучения. Поэтому
 (1.6)
(1.6)
Ещё раз обратим внимание на то, что формулы (1.5) и (1.6) справедливы только для случая нормального падения света на поверхность. Расчет давления света при наклонном падении лучей проведен в задаче № 5.
2. Фотоэлектрический эффект. Вообще говоря под фотоэлектрическим эффектом (фотоэффектом) понимают целую группу явлений. Мы выделим среди них только два - внешний и внутренний фотоэффекты.
Внешним фотоэффектом называется испускание электронов веществом при его облучении светом. На рис.1 приведена вольтамперная характеристика фотоэффекта-зависимость фототока I от напряжения U между электродами. 
 Для того, чтобы фототок стал равным нулю, необходимо приложить задерживающее напряжение Uo (рис.1). Очевидно, что
Для того, чтобы фототок стал равным нулю, необходимо приложить задерживающее напряжение Uo (рис.1). Очевидно, что
eUo=T (1.8)
где Т - максимальная кинетическая энергия фотоэлектронов. В случае Т<<Е0, где Е0=m0c2 энергия покоя электрона, Т=meυ2/2. Если же кинетическая энергия электрона T сравнима с энергией покоя электрона (@ 0.511 МэВ), то необходимо пользоваться релятивистскими формулами
 (1.9)
(1.9)
где b=υ/c.
Исследованиями установлены три закона внешнего фотоэффекта:
1. При фиксированной частоте падающего света сила фототока насыщения пропорциональна энергетической освещенности катода.
2. Максимальная начальная кинетическая энергия фотоэлектронов прямо пропорциональна частоте n падающего света.
3. Каждое вещество имеет свою собственную “красную границу” фотоэффекта, т.е. минимальную частоту n0 (или максимальную длину волны l0) света, при которой свет любой интенсивности уже не вызывает фотоэффекта.
Последние два закона фотоэффекта полностью описываются уравнением Эйнштейна для внешнего фотоэффекта: hn=Aв+T (1.10),
где Ав - так называемая работа выхода электрона -т.е. работа, которую необходимо затратить для удаления электрона из вещества. Данная работа является индивидуальной характеристикой любого химического элемента.
Внутренним фотоэффектом называется переход электронов в полупроводнике или диэлектрике, из связанных состояний в свободное под действием светового излучения без вылета за пределы образца. Явление внутреннего фотоэффекта обусловлено тем, что в полупроводниках и диэлектриках работа выхода электрона складывается из двух частей: а) работы, необходимой для отрыва электрона от атома и б) работы, необходимой для удаления его из образца. Если энергия кванта превышает сумму этих работ, то наблюдается внешний фотоэффект, если энергия кванта меньше, но больше ширины запрещёной зоны то имеет место внутренний фотоэффект.
3. Эффект Комптона заключается в том, что при рассеянии жесткого (коротковолнового) электромагнитного излучения на свободных электронах происходит увеличение длины волны рассеянного света. Разность длин волн Dl=l/-l, получившая название комптоновского сдвига
 (1.11)
(1.11)
где q - угол рассеяния (см. рис. 2), m0 - масса покоя электрона. Величина lc=h/m0c называется комптоновской длиной волны частицы массой m0 . Для электрона lc=2.426 ∙ 10-12 м.. Заметим, что в эффекте Комптона электрон практически всегда является релятивистской частицей из-за очень короткой длины волны рентгеновского и g - излучений, которые обусловливают это явление.





|
|
|
|
|
|
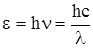 a Bрасрассеянный фотон
a Bрасрассеянный фотон




 падающий фотонajnjyффотон
падающий фотонajnjyффотон
mυ электрон
Рис. 2
II. Примеры решения задач.
 Задача №1.
Задача №1.

Решение. 
Решим предложенную задачу в несколько более общем виде, чем она сформулирована. То есть определим количество фотонов Nп поглощаемых поверхностью произвольного размера S, за произвольный промежуток времени t.
Очевидно, что
 (1)
(1) 
где N ' то же, что и Nп для единичных S и t. Обратим внимание на то, что Nп' - это число поглощенных фотонов, которое связано с N в формуле (1.5) - числом падающих фотонов простыми соотношением Nп' =N (1-a). Откуда, с учетом (1) получаем:


 (2)
(2) 
Подставляя формулу (2) в (1.5) имеем
 (3)
(3)
Заменяем в этой формуле частоту излучения на его длину волны (n=c/l) и выражаем искомую величину:
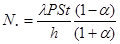 (4)
(4)
Подставляя в эту формулу входящие в нее величины, выраженные в системе СИ, и проведя вычисления, получаем значение N = 1.1 ∙ 1016 (фотонов).

Задача №2.

число N фотонов, падающих на нее за время t=5c.
Решение.
Сила светового давления на поверхность равна произведению светового давления P на площадь S поверхности:
F = P∙ S (1)
Давление света определим по формуле (1.6):
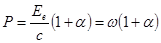 (2)
(2)
Подставляя это выражение в формулу (1), получим:
 (3)
(3)
Поскольку произведение энергетической светимости Ее на площадь S поверхности равно потоку Ф энергии излучения, падающего нормально на поверхность, то последнее можно переписать в виде
 (4)
(4)
Число N фотонов, падающее за время Dt на поверхность, можно определить по формуле
 (5)
(5)
где DW - энергия, получаемая поверхностью за время Dt. Очевидно, что DW=Ф*Dt. Тогда:  (6)
(6)
Для энергии кванта используем формулу (1.1) и получаем окончательно
 (7)
(7)
Формулы (3) и (4) являются расчетными. Подставив числовые значения в единицах СИ, и учитывая, что a=1 (поверхность зеркальная), находим, что
F=4∙ 10 -9Н= 4 нН, N=1019 (фотонов).
 |
Задача №3.

Решение.






|


 |
|





 От спектрального состава света егодавление
От спектрального состава света егодавление



 х не зависит (см.формулу (1.6)), поэтому для
х не зависит (см.формулу (1.6)), поэтому для

 простоты будем считать его монохроматическим
простоты будем считать его монохроматическим
 Сначала найдём силу dF, действующую на
Сначала найдём силу dF, действующую на
Рис.3 элементарное кольцо dS (Рис. 3) в направлении оси X. При зеркальном отражении каждый фотон передаёт поверхности импульс Dp = 2p cosq, проекция которого на ось Х D p х = 2p cos 2q, где p =  . Поток фотонов dN, падающих ежесекундно на кольцо dS, равен dN = (I / hn)
. Поток фотонов dN, падающих ежесекундно на кольцо dS, равен dN = (I / hn)  · cos q, где dS = 2pR2 sinq dq. Тогда d F = D p х
· cos q, где dS = 2pR2 sinq dq. Тогда d F = D p х 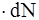 = 4p R2 (I / c) cos 3q sin q dq. Проинтегрировав это выражение по, от 0 до p /2, получим F = pR2 I / c.
= 4p R2 (I / c) cos 3q sin q dq. Проинтегрировав это выражение по, от 0 до p /2, получим F = pR2 I / c.
|
 такой высоте, что
такой высоте, что
Решение.
Аналогично ходу решения предыдущей задачи, искомую силу F будем искать как произведение
F = P ∙ S (1)
где P – давление солнечного света, S- площадь поверхности, нормальной к солнечным лучам; для шарообразного спутника эта площадь всегда равна
Давление света определяется формулой (1.6), в которую входит величина Еe -
энергетическая освещённость данной поверхности, которая по своему смыслу (при
нормальном падении светового луча) совпадает с интенсивностью I излучения – см. формулу (1.8) первой части данного пособия [ 7 ].А величина I для солнечного излучения есть солнечная постоянная, экспериментальное значение которой равно
1.4 кВ/м2 -см. задачу № 7 там же. С учётом этого и формулы (1.6) выражение для определяемой силы (3) переписываем в виде:
|
|
Подставляем в эту формулу числовые значения величин, выраженные в единицах системы СИ, и получаем искомый результат:
F = 10.3 . 10 –3 Н = 10.3 мН.

Задача № 5.

Решение.
Если бы свет падал на зеркало нормально (j=0), то давление света Ро выражалось бы формулой (1.6). Так как при этом Ее=I (см. предыдущую задачу), то можно записать
 (1)
(1)
Используя квантовые представления о свете, определим зависимость давления Р от угла падения j. Исходя из определения давления и применив к зеркалу второй закон Ньютона, запишем
 (2)
(2)
где 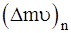 - проекция импульса
- проекция импульса  , сообщенного фотоном за время Dt зеркалу, на на направление нормали к нему, S - площадь освещенной поверхности. По закону сохранения импульса величина
, сообщенного фотоном за время Dt зеркалу, на на направление нормали к нему, S - площадь освещенной поверхности. По закону сохранения импульса величина  численно равна суммарному значению импульса
численно равна суммарному значению импульса  всех фотонов при их взаимодействии с зеркалом за время Dt. Следовательно,
всех фотонов при их взаимодействии с зеркалом за время Dt. Следовательно,  (3)
(3)
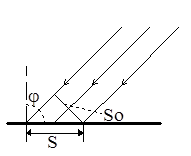 Рис.4.
Рис.4. 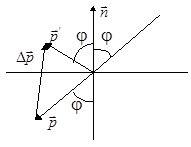 Рис.5
Рис.5
Величины S и (Dp)n зависят от угла падения j. Как видно из Рис.4
 (4)
(4)
где So - площадь поперечного сечения светового пучка. На рис.5. изображены суммарные импульсы фотонов, падающих на поверхность и отраженных от него (за время Dt): 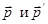 , так что
, так что  .
.
Переходя от этого векторного равенства к проекциям на направление нормали  к зеркалу и учитывая противоположные направления проекций
к зеркалу и учитывая противоположные направления проекций  , запишем
, запишем
 (5)
(5)
Подставляя (3) и (4) в (2), получаем
 (6)
(6)
Заметим, что при j=0, р = ро и тогда из (1) следует, что
 (7)
(7)
и теперь формулу (5) переписываем в окончательном виде:
 (8)
(8)
Выразим в единицах СИ входящие в формулу (8) величины, выполним вычисления и получим p=3.17 ∙ 10-4 Па
 Задача № 6
Задача № 6

Решение.
Давление, производимое светом при нормальном падении, Р0 = ω (1+ ρ), где
ρ – коэффициент отражения. Для зеркала коэффициент отражения ρ = 1. Сила све-
тового давления на поверхность равна: F = P0 ∙ ∆S = 2ω ∙ ∆S.
Согласно второму закону Ньютона запишем:
Fn =  и Fτ =
и Fτ =  , где (∆ P) τ и
, где (∆ P) τ и  (∆ P) n - проекции импульса
(∆ P) n - проекции импульса
|
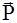 , сообщённые фотонами зеркалу за время ∆ t в тангенциальном и нормальном направлениях соответственно.
, сообщённые фотонами зеркалу за время ∆ t в тангенциальном и нормальном направлениях соответственно.


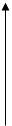



 ∆
∆ 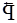 q q
q q
 |
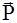
Рис. 6
циальная и нормальная составляющие силы, с которой падающий под углом θ
к нормали световой пучок действует на идеальное зеркало, равны: F τ = 0 и Fn = P0 ∙ ∆S ∙ cos θ = 2 ω ∙ ∆S ∙ cos θ.
Внешний фотоэффект
Задача № 7. Изобразить зависимость фототока насыщения i н от напряжённости
электрического поля Е в падающей световой волне.
Решение.
Согласно закону Столетова, фототок насыщения i н пропорционален интенсивности падающего света. В свою очередь, интенсивность света пропорциональна квадрату амплитуды световой волны. Световым вектором является вектор напряжённости электрического поля  . Следовательно, i н @ aE2 ,
. Следовательно, i н @ aE2 ,

 i н i н = aE2
i н i н = aE2


Е  Рис.7
Рис.7
 Задача № 8.
Задача № 8.

электрического поля достигает U=1.00В. Определите работу выхода в электронвольтах и красную границу фотоэффекта для цезия.
Решение.
Запишем уравнение Эйнштейна (1.10) для внешнего фотоэффекта.
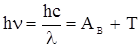 (1)
(1)
Так как даже самые быстрые электроны задерживаются электрическим полем, пролетев в нем расстояние, соответствующее разности потенциалов U, то их максимальная начальная кинетическая энергия связана с величиной задерживающего напряжения Uo соотношением (1.8). Следовательно:
 (2)
(2)
Отсюда находим работу выхода электронов:
 (3)
(3)
При облучении светом, длина волны которого lкр соответствует красной границе фотоэффекта, скорость, а следовательно, и кинетическая энергия фотоэлектронов равны нулю. Поэтому уравнение Эйнштейна для фотоэффекта (1) в случае красной границы запишется в виде:
 , Отсюда
, Отсюда  (4)
(4)
Формулы (3) и (4) являются расчетными. Выразим входящие в них величины в единицах СИ и проведем вычисления. В результате получаем:
AB=4.626*10-19-1.602*10-19=3.024*10-19 Дж=1.89эВ и lкр=657нм.
 Задача № 9.
Задача № 9.

Решение.
Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для внешнего фотоэффекта (1.10):
 (1)
(1)
Работа выхода электрона AB указана в таблице, приведенной в приложении. Для серебра AB=4.74эВ.
Кинетическая энергия фотоэлектрона, в зависимости от того, какая скорость ему сообщается, может быть выражена (см. приложение к формуле (1.8)) или по классической формуле
 (2)
(2)
или по релятивистской (1.9):

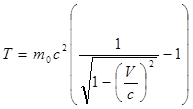 (3)
(3)
Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия фотона e много меньше энергии покоя электрона Е0, то может быть применена формула (2). Если же e сравнима по величине с Е0, то вычисления необходимо проводить по формуле (3).
1. Определим энергию падающего фотона в случае ультрафиолетового излучения:

Это значение энергии фотона много меньше энергии покоя электрона (0.511МэВ). Следовательно, для данного случая максимальная кинетическая энергия фотоэлектрона в формуле (1) может быть выражена по классической формуле (2). Тогда  (4)
(4)
Откуда получаем
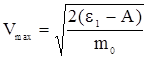 (5)
(5)
Подставляем в формулу (5) величины, выраженные в единицах СИ и находим максимальную скорость:
Vmax=1.08*106 м/с.
2. Теперь вычислим энергию фотона g - излучения:
 (6)
(6)
Работа выхода электрона (А=4.7эВ) пренебрежимо мала по сравнению с энергией g - кванта, поэтому можно считать, что максимальная кинетическая энергия электрона
равна энергии фотона. Так как в данном случае кинетическая энергия электрона
сравнима с его энергией покоя, то для вычисления скорости электрона следует использовать релятивистскую формулу (3). Выполнив преобразования, получим b=0.755.
Следовательно, максимальная скорость фотоэлектронов, вырываемых g - излучением
Vmax=c· b=2.26*108 м/с
 Задача № 10.
Задача № 10.

пластинкой, то задерживающую разность потенциалов придется увеличить до 4.28 В. Определите работу выхода Ав электронов с поверхности этой пластинки.
Решение.
В условии данной задачи не приведена длина волны или частота использованного излучения. Однако эту трудность легко обойти. Запишем уравнение Эйнштейна для внешнего фотоэффекта (1.10) для обоих случаев.

 (1)
(1)
где АВ1; АВ2 – работа выхода электрона из платиновой пластинки и второго металла; Т1;Т2 – максимальная кинетическая энергия электронов в первом и втором случаях. Поскольку равны левые части записанных уравнений, то равны и правые их части. Приравнивая их, находим  (2)
(2)
Мы уже знаем, что фототок может блокироваться некоторой разностью потенциалов, приложенной к электродам. Причем, величина фототока станет равной нулю, когда eU=T (см. (1.8) и задачу № 8). С учетом этого формула (2) преобразуется к виду  (3)
(3)
Величину работы выхода электрона для платины возьмем из таблицы в приложении (АВ1=5,3 эВ). Подставляем исходные данные в формулу (3) и получаем результат АВ2=4,74 эВ=7,58*10-19Дж.
Из металлов, для которых приведены сведения по АВ в таблице приложения наиболее близкое значение работы выхода имеет серебро. Делаем вывод о том, что вторым металлом в данном эксперименте может быть серебро.
 |
Задача № 11.

|
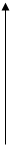
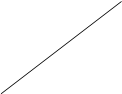
 U3
U3


 О ν
О ν
Рис. 8.
Для прекращения фототока необходимо приложить задерживающее напряжение U3,
определяемое выражением T= e ∙ U3, где T – максимальная кинетическая энергия фотоэлектрона и e –заряд электрона.Таким образом,  (1).
(1).
Разные прямые на рисунке получены для различных материалов фотокатода, имеющих разные величины работы выхода. Значения работы выхода для каждого
материала можно определить либо по пересечению с осью абсцисс: Ав = h∙ν0 ,
(здесь ν0 - красная граница фотоэффекта), либо по пересечению с осью ординат:
Ав = – e ∙ U3 0. Угловой коэффициент наклона прямых равен 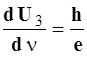 (2).
(2).
Следовательно, полагая известной величину e, возможно определить постоянную Планка h.
Эффект Комптона.
 Задача № 12.
Задача № 12.

|

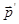 = h / λ ∕
= h / λ ∕
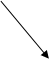

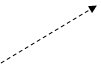
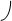


q
j
Запишем формулу, определяющую изменение
|
|

Комптона (1.11):
|
|
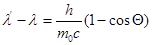 (1)
(1)
Так как нас в этой задаче интересует энергия квантов, то в соответствии с формулой (1.1) 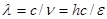 перепишем (1) в более удобном виде:
перепишем (1) в более удобном виде:
 (2)
(2)
где Е0 – энергия покоя электрона (Е0=0,511 МэВ)
Сократим полученное равенство на hc и учтем, что по условию  . Тогда
. Тогда  (3)
(3)
Откуда 
Для нахождения импульса вспомним формулу (1.4):
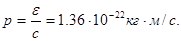
 Задача № 13.
Задача № 13.

Решение.
Для определения энергии первичного фотона запишем формулу для эффекта Комптона в виде (1.11):
 (1)
(1)
Последовательность дальнейших преобразований во многом аналогична преобразованиям в предыдущей задачи за исключением того, что искомой величиной является e:
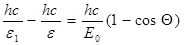 Отсюда
Отсюда 
И окончательно:  (2)
(2)
Как и в предыдущей задаче вычисления по формуле (2) удобнее провести во внесистемных единицах (в МэВ). Подставляем числовые данные и получаем
e = 2,513 МэВ = 4,021*10-14 Дж.
 Задача №14.
Задача №14.

Решение.
1. Эта часть задачи не вызывает никаких затруднений, поскольку аналогичный вопрос разбирался в предыдущих двух задачах. Отметим только, что исходной является формула для эффекта Комптона (1.11), а итоговая формула выглядит так: 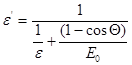 (1)
(1)
Подставив числовые значения величин, получим

2. Кинетическая энергия электрона отдачи, как это следует из закона сохранения энергии, равна разности между энергией e падающего фотона и энергией e/ рассеянного фотона: Т=e-e/=0,32 МэВ.
3. Направление движения электрона отдачи определим, применив закон сохранения импульса, согласно которому импульс падающего фотона  равен векторной сумме импульса рассеянного фотона
равен векторной сумме импульса рассеянного фотона  и электрона отдачи
и электрона отдачи  :
:  (2)
(2)
 Векторная диаграмма импульсов изображена на рис.9.
Векторная диаграмма импульсов изображена на рис.9.
 | |||
 |
Рис. 9
 или
или 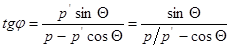 (3)
(3)
Так как  и
и 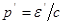 , то
, то
 (4)
(4)
Преобразуем формулу (4) так, чтобы угол j выражался непосредственно через величины e и q, заданные в условии задачи. Из формулы (1) следует
 (5)
(5)
Теперь подставим (5) в формулу (4)
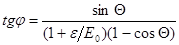 (6)
(6)
Формула (6) является расчетной. Однако её можно слегка упростить, воспользовавшись известными тригонометрическими формулами:  и
и 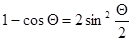 . Подставляем эти выражения в (4) и после элементарных преобразований получаем:
. Подставляем эти выражения в (4) и после элементарных преобразований получаем:  (7)
(7)
Вычисления по формуле (7) дают значение  , откуда искомый угол j=350.
, откуда искомый угол j=350.
 Задача № 15.
Задача № 15.

|
 Решение.
Решение.

 ν2 θ2 ν1 θ1
ν2 θ2 ν1 θ1


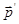
 -
-  =
=  , то (∆
, то (∆  τ -
τ -  τ =
τ =  , где
, где  ,
а Vm – максимальная скорость фотоэлектрона и
А в – работа выхода электрона из катода.
,
а Vm – максимальная скорость фотоэлектрона и
А в – работа выхода электрона из катода.
 = h / λ
= h / λ

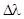 =
=  (1).
Отсюда видно, что при θ = θ2 изменение длины волны, по сравнению с первоначальной больше,
чем в случае когда θ = θ1 . Следовательно, можно записать неравенство: hν2 ‹ hν1 (2) .
(1).
Отсюда видно, что при θ = θ2 изменение длины волны, по сравнению с первоначальной больше,
чем в случае когда θ = θ1 . Следовательно, можно записать неравенство: hν2 ‹ hν1 (2) .