ГЛАВА 4. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ
Магнитная индукция
В 1820 году Эрстед обнаружил, что поле, возбуждаемое проводниками с током, оказывает ориентирующее действие на магнитную стрелку (отсюда название магнитное поле). Стрелка всегда устанавливается в магнитном поле определенным образом (по силовым линиям поля).
Магнитное поле создается: движущимися зарядами, проводниками с током, телами, обладающими магнитным моментом (постоянными магнитами) и действует на эти же объекты.
В природе не существует магнитного аналога элементарному электрическому заряду. Пробным телом, пригодным для определения и измерения магнитного поля, может быть элементарный плоский контур с током (пробный ток), магнитным полем которого можно пренебречь.
Количественной характеристикой элементарного плоского контура с током является его магнитный момент:
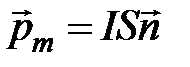 , (4.1)
, (4.1)
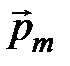
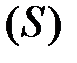
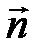
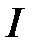
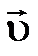
 где
где 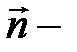 единичный вектор нормали к плоскости контура, образующий правый винт с направлением тока;
единичный вектор нормали к плоскости контура, образующий правый винт с направлением тока;

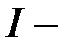 сила тока, протекающего по контуру;
сила тока, протекающего по контуру; 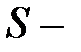 площадь поверхности, ограниченной контуром.
площадь поверхности, ограниченной контуром.
Если поместить пробный ток в магнитное поле, созданное внешним источником, то пробный ток будет испытывать силовое воздействие поля, его магнитный момент будет устанавливаться в поле определенным образом.
Механический момент сил 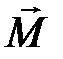 , который поворачивает
, который поворачивает 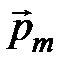 в магнитном поле будет равен
в магнитном поле будет равен
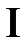
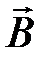
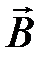
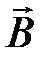
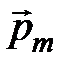
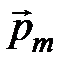
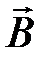
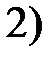
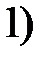
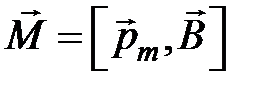 . (4.2)
. (4.2)
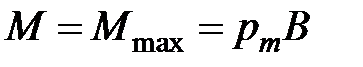 , когда
, когда 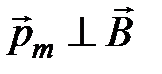 , см. 1)
, см. 1)
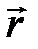
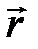 Отношение
Отношение 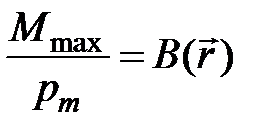 называют модулем магнитной индукции в точке
называют модулем магнитной индукции в точке 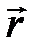 . Вектор магнитной индукции
. Вектор магнитной индукции 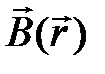 сонаправлен с
сонаправлен с 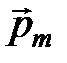 в равновесном положении контура, когда
в равновесном положении контура, когда 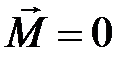 .
.
Это будет при 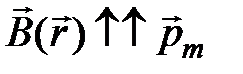 , см. 2) на рисунке. За направление
, см. 2) на рисунке. За направление 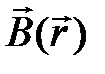 и берут это направление.
и берут это направление.
Если ток, создающий магнитное поле стационарный (постоянный), то такое поле называют магнитостатическим.
Магнитостатическое поле изображают с помощью линий магнитной индукции, касательные к которым в каждой точке совпадают с вектором 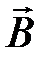 Линии магнитной индукции всегда замкнуты и охватывают проводники с током.
Линии магнитной индукции всегда замкнуты и охватывают проводники с током.
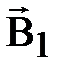
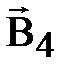
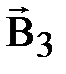
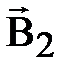
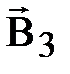
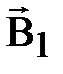
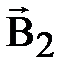
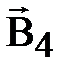
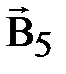
Магнитное поле беско-
Магнитное поле постоян- нечно длинного прямолинейного ного магнита. проводника с током.
Индукция магнитного поля заряда 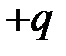 , движущегося с постоянной скоростью
, движущегося с постоянной скоростью 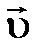 в точке
в точке 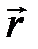 (см. рисунок ниже), в случае (
(см. рисунок ниже), в случае ( ):
):

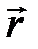
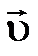
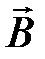

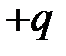

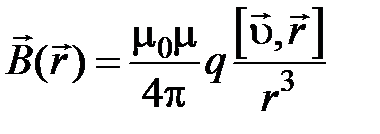 , (4.3)
, (4.3)
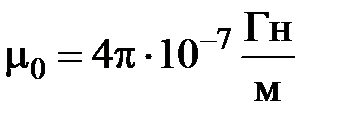 – магнитная постоянная,
– магнитная постоянная,
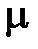 – магнитная проницаемость среды, для вакуума
– магнитная проницаемость среды, для вакуума 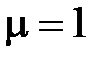 .
.
Модуль 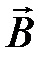 равен
равен 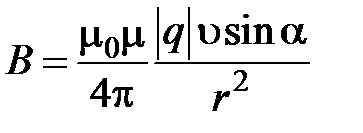 .
.
В СИ: 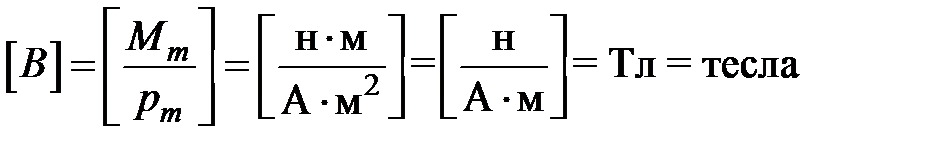 .
.

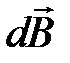
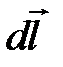
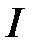
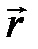
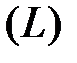


 4.2. Магнитное поле проводника с током.
4.2. Магнитное поле проводника с током.
Закон Био–Савара–Лапласа
Пусть по длинному тонкому проводнику, идет ток 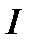 . Элемент линейного тока
. Элемент линейного тока 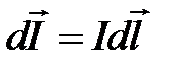 , направленный по току, создаст в некоторой точке
, направленный по току, создаст в некоторой точке 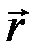 магнитное поле, индукция которого
магнитное поле, индукция которого 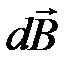 равна:
равна:
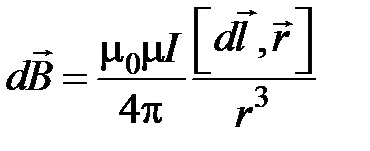 (4.4)
(4.4)
Формула (4.4) – закон Био–Савара–Лапласа.
Модуль вектора 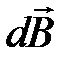 определяется выражением
определяется выражением
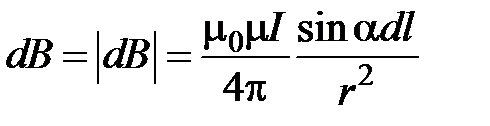 (4.5)
(4.5)
где 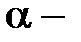 угол между вектором
угол между вектором 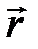 и направлением тока в элементе провода.
и направлением тока в элементе провода.
Магнитная индукция поля всего проводника с током:
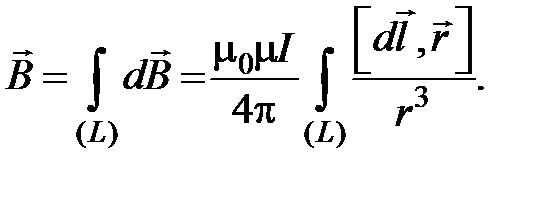
(4.6)
Формула (4.6) следует из принципа суперпозиции магнитных полей: магнитная индукция поля, создаваемого несколькими токами или движущимися зарядами в точке, равна векторной сумме индукций магнитных полей, создаваемых каждым током или движущимся зарядом в точке в отдельности, т.е.
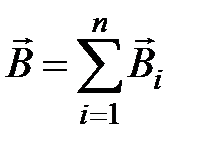 (4.7)
(4.7)
(4.7) – математическая запись принципа суперпозиции магнитных полей.
Для длинного проводника с током
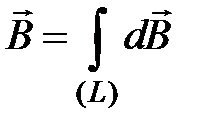 .
.
Если проводник и точка наблюдения лежат в одной плоскости, то 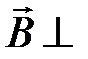 этой плоскости и все
этой плоскости и все 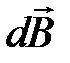 от различных элементов тока сонаправлены, тогда
от различных элементов тока сонаправлены, тогда
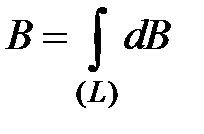 .
.
4.3. Поток вектора 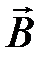 . Теорема Гаусса для вектора
. Теорема Гаусса для вектора 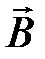
Поток любого вектора через поверхность можно представить, как
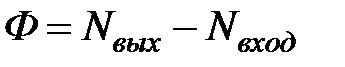 ,
,
где 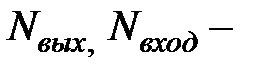 число выходящих и входящих силовых линий поля.
число выходящих и входящих силовых линий поля.
Магнитный поток вектора 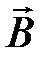 через произвольную поверхность
через произвольную поверхность 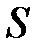 равен:
равен:
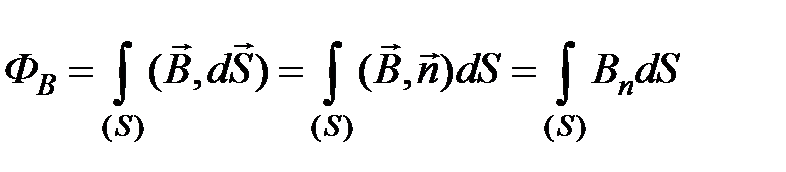 , (4.8)
, (4.8)
где 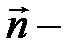 единичный вектор нормали к поверхности
единичный вектор нормали к поверхности 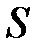 в данной точке.
в данной точке.
Единица магнитного потока в СИ:  =
= 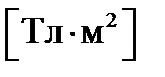 = вебер (Вб).
= вебер (Вб).
Поток вектора 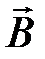 через любую замкнутую поверхность (S) равен нулю:
через любую замкнутую поверхность (S) равен нулю:
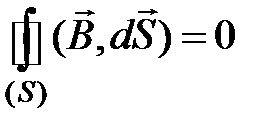 . (4.9)
. (4.9)
(4.9) – теорема Гаусса для вектора 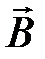 в интегральной форме.
в интегральной форме.
Используя теорему Остроградского-Гаусса для вектора 
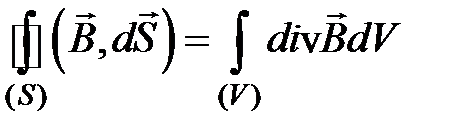 ,
,
можно получить
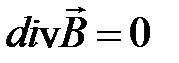 . (4.10)
. (4.10)
(4.10) – теорема Гаусса для вектора 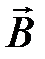 в дифференциальной форме.
в дифференциальной форме.
Из (4.9) и (4.10) следует, что в природе отсутствуют магнитные заряды – точечные магнитные однополюсники (монополи).
4.4. Циркуляция вектора Циркуляция вектора где Циркуляция вектора (4.12) – теорема о циркуляции вектора При этом ток Если ток распределен по поверхности Тогда (4.12) можно переписать в виде Используя теорему Стокса для вектора можно получить (4.13) – теорема о циркуляции вектора Из (4.12) и (4.13) следует, что магнитное поле является вихревым, не потенциальным. Сила Лоренца Сила, действующая на заряженную частицу в электромагнитном поле. где Если Если модуля скорости частицы, но может, в зависимости от траектории, менять направление скорости. Покажем, что магнитное поле не может ускорить частицу. Сила Лоренца И всегда В однородном магнитном поле траекторию движения частицы задает угол если если если 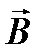 . Теорема о циркуляции вектора
. Теорема о циркуляции вектора 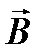 (закон полного тока)
(закон полного тока)
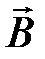 по произвольному контуру
по произвольному контуру 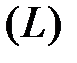 равна
равна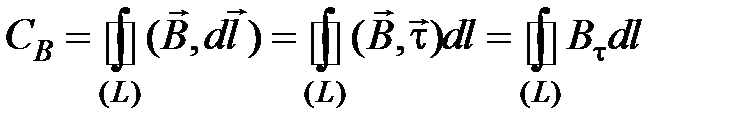 , (4.11)
, (4.11)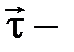 единичный вектор, касательный к контуру
единичный вектор, касательный к контуру 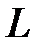 .
.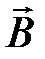 по произвольному замкнутому контуру
по произвольному замкнутому контуру 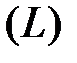 равна произведению
равна произведению 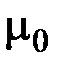 на алгебраическую сумму токов, охватываемых этим контуром:
на алгебраическую сумму токов, охватываемых этим контуром: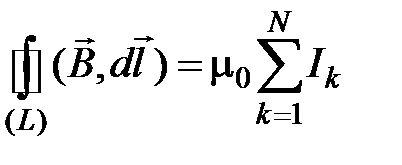
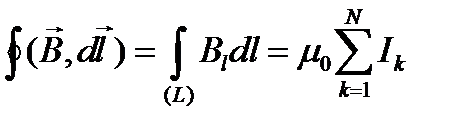 . (4.12)
. (4.12)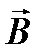 в интегральной форме (закон полного тока).
в интегральной форме (закон полного тока).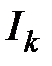 считается положительным, если он образует правый винт с выбранным направлением обхода контура, и отрицательным
считается положительным, если он образует правый винт с выбранным направлением обхода контура, и отрицательным 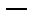 если левый.
если левый.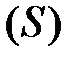 с плотностью
с плотностью  , то
, то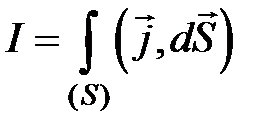 .
.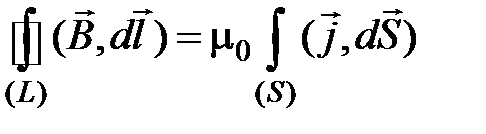 .
.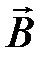 :
: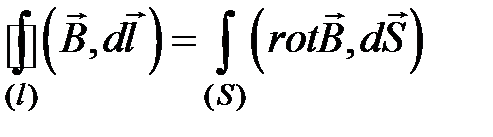 ,
,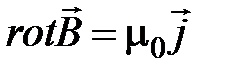 . (4.13)
. (4.13)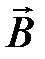 в дифференциальной форме.
в дифференциальной форме. , (4.14)
, (4.14)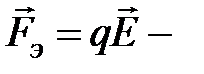 электрическая составляющая силы Лоренца,
электрическая составляющая силы Лоренца,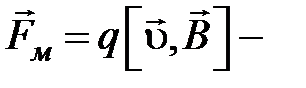 магнитная составляющая силы Лоренца. (4.15)
магнитная составляющая силы Лоренца. (4.15)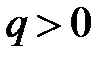 , то
, то 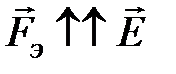 ,
,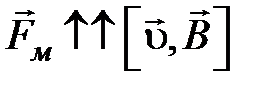 .
.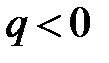 , то
, то 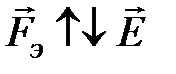 ,
,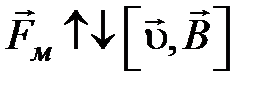 .
.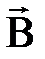
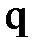
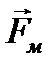
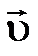
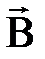
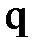
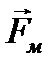
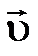
 Магнитная составляющая силы Лоренца
Магнитная составляющая силы Лоренца 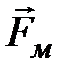 (гироскопическая сила) всегда направлена перпендикулярно скорости движения заряда
(гироскопическая сила) всегда направлена перпендикулярно скорости движения заряда 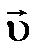 , поэтому она работы над зарядом не совершает, и кинетическая энергия заряженной частицы при движении в магнитном поле не меняется, т.е.
, поэтому она работы над зарядом не совершает, и кинетическая энергия заряженной частицы при движении в магнитном поле не меняется, т.е. 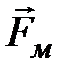 не изменяет
не изменяет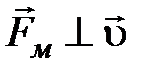 . Работа магнитной составляющей силы Лоренца по определению:
. Работа магнитной составляющей силы Лоренца по определению: 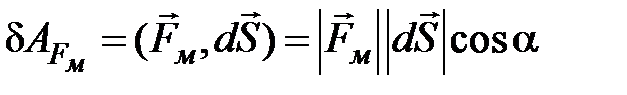 .
.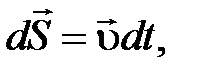 т.е.
т.е. 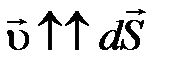 , а
, а 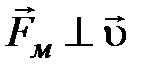 (по определению). Следовательно, для силы Лоренца
(по определению). Следовательно, для силы Лоренца 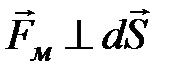 , т.е.
, т.е. 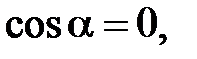 откуда
откуда 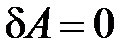 , а т.к.
, а т.к. 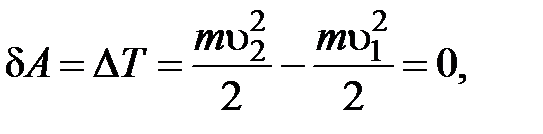 это значит, что
это значит, что 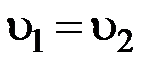 , т.е.
, т.е. 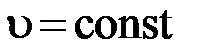 . Отсюда магнитное поле
. Отсюда магнитное поле 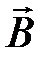 не меняет величину скорости частицы. Величину скорости частицы изменяет электрическое поле
не меняет величину скорости частицы. Величину скорости частицы изменяет электрическое поле 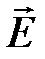 .
.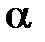 между векторами
между векторами 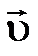 и
и 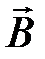 :
: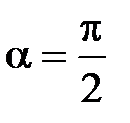 , траекторией движения частицы является окружность;
, траекторией движения частицы является окружность;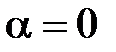 , частица движется вдоль силовых линий
, частица движется вдоль силовых линий 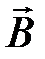 по прямой;
по прямой; – любой другой угол, частица движется по винтовой линии (спирали).
– любой другой угол, частица движется по винтовой линии (спирали).