Алгоритмы устойчивой сортировки
· Сортировка выбором (Selection sort) — Сложность алгоритма: O(n 2); поиск наименьшего или наибольшего элемента и помещение его в начало или конец упорядоченного списка
· Сортировка пузырьком (англ. Bubble sort) — сложность алгоритма: O(n2); для каждой пары индексов производится обмен, если элементы расположены не по порядку.
· Сортировка перемешиванием (Шейкерная, Cocktail sort, bidirectional bubble sort) — Сложность алгоритма: O(n 2)
· Гномья сортировка — имеет общее с сортировкой пузырьком и сортировкой вставками. Сложность алгоритма — O(n 2).
· Сортировка вставками (Insertion sort) — Сложность алгоритма: O(n 2); определяем где текущий элемент должен находиться в упорядоченном списке и вставляем его туда
· Сортировка слиянием (Merge sort) — Сложность алгоритма: O(n log n); требуется O(n) дополнительной памяти; выстраиваем первую и вторую половину списка отдельно, а затем — сливаем упорядоченные списки
· Сортировка с помощью двоичного дерева (англ. Tree sort) — Сложность алгоритма: O(n log n); требуется O(n) дополнительной памяти
· Алгоритм сортировки Timsort (англ. Timsort) — Сложность алгоритма: O(n log n); требуется O(n) дополнительной памяти; Комбинированный алгоритм (используется сортировка вставками и сортировка слиянием.
· Сортировка подсчётом (Counting sort) — Сложность алгоритма: O(n + k); требуется O(n + k) дополнительной памяти (рассмотрено 3 варианта)
· Блочная сортировка (Корзинная сортировка, Bucket sort) — Сложность алгоритма: O(n); требуется O(k) дополнительной памяти и знание о природе сортируемых данных, выходящее за рамки функций "переставить" и "сравнить".
Алгоритмы неустойчивой сортировки
· Сортировка Шелла (Shell sort) — сложность алгоритма: 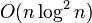 ; попытка улучшить сортировку вставками
; попытка улучшить сортировку вставками
· Сортировка расчёской (Comb sort) — сложность алгоритма: 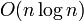
· Пирамидальная сортировка (сортировка кучи, Heapsort) — сложность алгоритма: 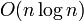 ; превращаем список в кучу, берём наибольший элемент и добавляем его в конец списка
; превращаем список в кучу, берём наибольший элемент и добавляем его в конец списка
· Плавная сортировка (Smoothsort) — сложность алгоритма: 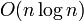
· Быстрая сортировка (Quicksort), в варианте с минимальными затратами памяти — сложность алгоритма: 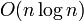 — среднее время,
— среднее время, 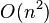 — худший случай; широко известен как быстрейший из известных для упорядочения больших случайных списков; с разбиением исходного набора данных на две половины так, что любой элемент первой половины упорядочен относительно любого элемента второй половины; затем алгоритм применяется рекурсивно к каждой половине. При использовании
— худший случай; широко известен как быстрейший из известных для упорядочения больших случайных списков; с разбиением исходного набора данных на две половины так, что любой элемент первой половины упорядочен относительно любого элемента второй половины; затем алгоритм применяется рекурсивно к каждой половине. При использовании 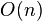 дополнительной памяти, можно сделать сортировку устойчивой.
дополнительной памяти, можно сделать сортировку устойчивой.
· Introsort — сложность алгоритма: 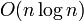 , сочетание быстрой и пирамидальной сортировки. Пирамидальная сортировка применяется в случае, если глубина рекурсии превышает
, сочетание быстрой и пирамидальной сортировки. Пирамидальная сортировка применяется в случае, если глубина рекурсии превышает 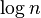 .
.
· Patience sorting — сложность алгоритма: 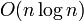 — наихудший случай, требует дополнительно
— наихудший случай, требует дополнительно 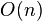 памяти, также находит самую длинную увеличивающуюся подпоследовательность
памяти, также находит самую длинную увеличивающуюся подпоследовательность
· Stooge sort — рекурсивный алгоритм сортировки с временной сложностью 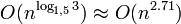 .
.
· Поразрядная сортировка (она же цифровая сортировка) — сложность алгоритма: 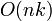 ; требуется
; требуется 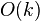 дополнительной памяти.
дополнительной памяти.