Опты короткого замыкания.

Электротехника

 

1. Резонанс токов.

Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.

Резонансом токов в цепи с параллельно соединенными индуктивностью и ёмкостью называется режим, при котором ток в неразветвленном участке цепи и напряжение, приложенное к этой цепи, совпадают по фазе.

Закон Ома для параллельного соединения активного сопротивления, емкости, индуктивности в общем случае выражается формулой:

bL и bc - реактивные проводимости, индуктивная и емкостная соответственно.

Угол сдвига фаз между током в неразветвленной части цепи I и приложенным напряжением:

Резонансная частота:

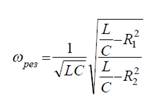
Общий реактивный ток, равный разности реактивных токов ветвей, при резонансе

токов равен 0.

Резонанс токов в отличие от резонанса напряжений не является опасным для

установок, поскольку в реальных условиях реактивные проводимости редко высокими.

Явления резонанса напряжений и токов широко используются в технике связи,автоматике и телемеханике, для улучшения cosφ в промышленных установках.

Путем настройки колебательного контура в резонанс с частотой передаваемого сигнала можно выделить полезный сигнал.

 

2. Расчет цепей синусоидального тока.

 

 

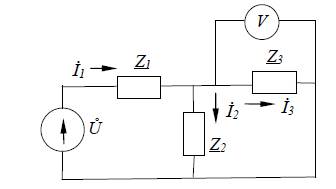
Сопростивление цепи в комплексом виде:

Затем токи в цепи:

Показания вольтметра:

Активная реактивная и полная мощности (S-полная мощность,P(действительная часть) – активная, Q(мнимая часть) – реативная часть:

 

Символьный метод:

Величины постоянного тока исчерпывающе определяются одним числом. Для определения величин переменного тока заданной частоты одного числа уже не достаточно, здесь необходимо два числа: амплитуда и начальная фаза. Однако и переменный ток может быть определён не 2-мя величинами, а одним комплексным числом, если воспользоваться символичным методом.

При его использовании для расчёта цепей переменная тока воспользуемся законами, методами и приёмами, рассмотренными ранее для цепей постоянного тока.Символический метод удобен и тем, что позволяет избежать построения векторных диаграмм. Он основан на использовании комплексных чисел.

 

 

1. Применение законов Ома, Кирхгофа для расчета электрических цепей переменного тока.

 

1. Трехфазные цепи, особенности соединений по схеме «звезда» и «треугольник»

Три взаимно связанные электрические цепи с ЭДС одинаковой частоты и амплитуды, но сдвинутые по фазе одна относительно другой на 1/3 периода называется трехфазной системой переменного тока.

Участок трехфазной системы, по которому протекает одинаковый ток, называется фазой.

Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и приемников или нагрузки, которые могут быть однофазными или трехфазными.

Если концы трех обмоток соединить в один узел, а начала будут служить для подключения нагрузки, то такой вид соединения называют соединения обмоток генератора звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным.

При таком способе соединения напряжение между каждой фазой и нулевым проводом называют фазным напряжением. Напряжение между фазами А-В, В-С, С-А называют линейным напряжением:

Если соединить конец первой обмотки с началом второй, конец второй – с началом третьей, конец третьей – с началом первой, то получим соединение треугольником. При этом узлы соединения являются отводами

При таком соединении нет различия между фазным и линейным соединением. Здесь появляется различие между фазными и линейными токами приемника.

Соотношение между фазными и линейными токами имеет следующую формулу:

Активная мощность трехфазного генератора равна сумме активных мощностей всех фаз:

Кодта звезда: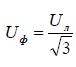

Когда треугольник:

 

Трехфазные цепи обладают следующими преимуществами:

- Экономичность передачи электроэнергии на значительные расстояния из-за меньшей материалоёмкости силовых кабелей, так как при одинаковой потребляемой мощности снижаются токи в фазах (по сравнению с однофазными цепями).

-Меньшая материалоёмкость 3-фазных трансформаторов.

-Уравновешенность системы. Это свойство является одним из важнейших, так как в неуравновешенной системе возникает неравномерная механическая нагрузка на энергогенерирующую установку, что значительно снижает срок её службы.

-Возможность простого получения кругового вращающегося магнитного поля, необходимого для работы электрического двигателя и ряда других

устройств. Двигатели 3-фазного тока (асинхронные и) устроены проще, чем двигатели постоянного тока, одно- или 2-фазные, и имеют высокие показатели экономичности.

-Возможность получения в одной установке двух рабочих напряжений — и линейного, и двух уровней мощности при соединении на «звезду» или «треугольник».

Благодаря этим преимуществам, трёхфазные системы наиболее распространены в современной электроэнергетике.

 

1. Резонанс напряжений.

В колебательных контурах при определенных условиях могут возникать особые явления, которые называют резонансными. Резонанс в последовательном колебательном контуре называют резонансом напряжений, резонанс в параллельном колебательном контуре – резонансом токов.

В цепях переменного тока резонанс наступает тогда, когда частота источника напряжения равна резонансной частоте контура. При резонансе ток и напряжение совпадают по фазе, т.е. угол φ = 0.

Рассмотрим цепь, состоящую из последовательно соединенных резистора, катушки индуктивности и конденсатора, Закон Ома для последовательной цепи, состоящей из активного, индуктивного и емкостного сопротивлений, выражается формулой:

Угол сдвига фаз между током и напряжением:

Резонанс наступает тогда, когда цепь ведет себя как чисто активная, т.е. когда ток и напряжение совпадают по фазе, угол φ = 0.

Условием возникновения резонанса в последовательном колебательном контуре является равенство реактивных сопротивлений контура.

Тогда полное сопротивление цепи будет равно его активной составляющей:

При резонансе напряжений действующие значения реактивных составляющих напряжения UL и UC равны по величине, мгновенные значения равны и противоположны по знаку.

Резонансная частота контура:

Резонанс напряжений можно получить изменяя в цепи индуктивность, емкость или частоту напряжения источника питания контура, всего, если хотят настроить контур в резонанс, используют конденсатор переменной емкости.

Поскольку резонанс сопровождается значительными перенапряжениями и сверхтоками, в мощных установках он является аварийным. Свойства колебательного контура характеризуются рядом величин:

 

Характеристическое сопротивление контура (или волновое):

Добротность последовательного контура:

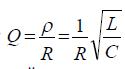
Затухание контура:

1. Трансформаторы, холостой ход и нагрузочный режим. Опыт короткого замыкания.

Трансформатором называется статичный (т.е. без движущихся частей) прибор, предназначенный чаще всего для преобразования одного переменного напряжения в другое напряжение той же частоты.

Трансформатор состоит из двух или более обмоток, которые связаны между собой через общий магнитный поток. Обмотки изолированы друг от друга (за исключением автотрансформаторов). Магнитная связь усиливается за счет сердечника, который состоит из листов электротехнической стали.

Обмотку трансформатора, которая соединяется с источником энергии, называют первичной. Обмотку, отдающую электроэнергию, а также величины, которые относятся к ней, называют вторичными. Соответственно все величины, характеризующие первичную обмотку, обозначают индексами 1, а вторичную — индексом 2.

Трансформаторы могут быть однофазным или трехфазным. Для трехфазного

трансформатора первичной или вторичной обмоткой называют три фазные обмотки одного напряжения. По способу охлаждения трансформаторы могут быть сухими или масляными. Щиток трансформатора содержит информацию о его номинальных напряжениях — высших и низших, номинальной и полной мощности, линейных токах, частоте, числе фаз, схеме и группе соединений и др. В случае, когда первичное напряжение U 1 меньше вторичного U 2, трансформатор называют повышающим, если U 1 > U 2, его называют понижающим. Для трансформатора отношение амплитудных, мгновенных и действующих значений э. д. с. соответствует отношению количеств витков обмоток трансформатора:

 

Существует несколько видов потерь в трансформаторе. Часть полезной мощности тратится на нагрев обмоток, так как их сопротивление не равно нулю. Существуют также потери в сердечнике, связанные с затратами энергии на перемагничивание, на рассеивание магнитного поля и вихревые токи. Несмотря на большое количество видов потерь, коэффициент полезного действия трансформатора очень высок и составляет 98-99.5%.

Холостым ходом называется такой режим трансформатора, при котором к зажимам его первичной обмотки подключено переменное напряжение, а вторичная обмотка разомкнута. Схема холостого хода показана на рисунке.

Этот режим применяется при испытании готового трансформатора. При холостом ходе первичное напряжение U 1 создается током холостого хода I 10, который создает магнитный поток Ф = Ф m sinω t. Вместе с тем происходит частичное рассеяние магнитного потока Фр1.

На векторной диаграмме трансформатора при холостом ходе изображаются

соотношения, подобные соотношениям в катушке со стальным сердечником, т. е. она повторяет векторную диаграмму катушки.

По опыту холостого хода можно вычислить коэффициент трансформации:

Мощность, которая потребляется трансформатором при холостом ходе, тратится на потери в сердечнике и потери в проводах только первичной обмотки i2

10R1. При этом почти все потери сводятся к потерям в стали, поэтому опыт холостого хода применяется для расчета потерь стали трансформатора.

 

Нагрузочный режим. При подключении нагрузки Z_H к вторичной обмотке трансформатора (рис. 222) он начинает отдавать нагрузке некоторую мощность. Соответственно увеличивается и мощность, получаемая первичной обмоткой из питающей сети. Следовательно, при увеличении тока i₂ во вторичной обмотке возрастает и ток i₁ в первичной обмотке.

Опты короткого замыкания.

Режим короткого замыкания трансформатора характеризуется тем, что вторичная обмотка замкнута накоротко или на очень малое сопротивление. Опыт короткого замыкания используют для нахождения параметров трансформатора: внутреннего падения напряжения, потерь в проводниках и т. п. При проведении этого опыта зажимы вторичной обмотки трансформатора накоротко замыкают и напряжение на первичной обмотке значительно понижают, при этом сила тока I1k в первичной обмотке равна номинальной.

1. Разветвленные цепи переменного тока. Параллельное включение RL и RC цепей. Активная, реактивная и полная проводимость данных цепей.

Для расчета цепи с параллельным соединением ветвей применяется метод

проводимостей.

Рассмотрим применение этого метода на примере расчета цепи, показанной на рисунке. Нужно определить общий ток I в неразветвленной цепи. Он равен векторной сумме токов параллельных ветвей.

При построении векторных диаграмм в случае параллельного соединения элементов в качестве исходного вектора используется вектор напряжения U, так как напряжение в этом случае одно и то же для всех ветвей.

Вектор тока Ī представляет собой сумму векторов тока ĪR, который совпадает с вектором напряжения U по фазе с вектором тока I L, отстающего от вектора напряжения U на угол π⁄2 и вектором тока I 2, опережающим напряжение на угол π⁄2.

Определим ток в цепи по первому закону Кирхгофа с учетом закона Ома для

проводимостей: Ī= ĪR+ ĪL+ ĪC=(G-jBL+jBC) Ů = YŮ,

где G=1/R; BL=1/ωL; BC=ωC - проводимости активного, индуктивного и емкостного элементов; Y – суммарная комплексная проводимость цепи, которая является обратной величиной комплексного сопротивления:

Таким образом, ток в цепи будет равен:

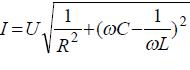
1. Расчет цепей постоянного тока при последовательном и параллельном включении источников и приемников энергии.

Для последовательной цепи, состоящей из нескольких элементов, строится векторная диаграмма напряжений. За исходный вектор принимается вектор тока, т.к. при последовательном соединении через все элементы цепи протекает один и тот же ток. Таким образом, векторная диаграмма напряжений для цепи с последовательно соединенными элементами R, L, C будет иметь вид, как показано на рис.

Вектор напряжения U, приложенного к цепи, определяется как сумма векторов ,а его величина равна:

Построим векторную диаграмму напряжений для цепи на рисунке. Для

произвольных значений сопротивлений R, XL и XC и тока I она будет иметь вид, показанный на рисунке.

Если модули векторов треугольника напряжений разделить на модуль вектора тока, то получим сопротивления последовательной цепи R, X, Z:

Эти сопротивления соотносятся как стороны прямоугольного треугольника.

Прямоугольный треугольник, стороны которого численно равны величинам R, X, Z, называется треугольником сопротивлений.

Таким образом,

Обычно для расчета электрических цепей используют комплексные числа. В комплексной форме полное напряжение записывается следующим образом:

Это соотношение есть закон Ома, записанный в комплексной форме. Сомножитель перед I есть полное сопротивление последовательной цепи в комплексной форме:

 

1. Переходные процессы при включении RC-цепи к постоянному напряжению.

Переходные процессы в цепи рис. 4.2 будут возникать при установке ключа К в положение 1 (нулевые начальные условия) или 2 (ненулевые начальные условия).

RC-цепь а) и переходные процессы в ней б) и в).

Переходной процесс в RC-цепи при нулевых начальных условиях. Рассмотрим случай, когда на входе цепи действует постоянное напряжение, т.е. u(t) = U. В момент t = 0 замкнем ключ К в положение 1 и подключим постоянное напряжение к цепи. Под действием напряжения U в цепи будет протекать ток i, который создает на резисторе R падение напряжения и заряжает емкость C. На основании второго закона Кирхгофа можно записать

Процесс перехода электрической цепи из одного состояния в другое (включение, выключение, переключение, изменение параметров элементов цепи и др.) называется переходным процессом. Любое скачкообразное изменение в цепи, приводящее к изменению установившегося режима, называют коммутацией. Длительностью процесса коммутации (включение, выключение и т.д.) обычно пренебрегают, то есть считают, что коммутация осуществляется практически мгновенно. А вот переход электрической цепи из одного установившегося режима в другой не может происходить мгновенно, на это требуется время (теоретически бесконечно большой отрезок времени). Например, включение электродвигателя. После нажатия кнопки «Пуск» (коммутация) двигатель приобретет нужную скорость не сразу. На разгон двигателя потребуется время. Еще пример, после подключения конденсатора к источнику электрической энергии (коммутации) конденсатор не сразу зарядится до напряжения источника. На это потребуется время. Примеров можно привести много и не только из области электротехники, но и из механики и любой другой области. Переходные процессы присущи всем явлениям природы.

Известно, что ток и напряжение идеального конденсатора в самом общем виде связаны следующим соотношением:

Тогда, согласно 2-му закону Кирхгофа, можно для схемы, приведенной на рис. 1, записать уравнение для мгновенных значений напряжений:

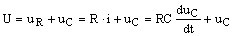
Получилось дифференциальное уравнение 1-го порядка:

 

1. Переходные процессы в цепях с индуктивностью: размыкание цепи с индуктивностью; включение RL цепи на постоянное напряжение.

Процесс перехода электрической цепи из одного состояния в другое (включение, выключение, переключение, изменение параметров элементов цепи и др.) называется переходным процессом. Любое скачкообразное изменение в цепи, приводящее к изменению установившегося режима, называют коммутацией. Длительностью процесса коммутации (включение, выключение и т.д.) обычно пренебрегают, то есть считают, что коммутация осуществляется практически мгновенно. А вот переход электрической цепи из одного установившегося режима в другой не может происходить мгновенно, на это требуется время (теоретически бесконечно большой отрезок времени). Например, включение электродвигателя. После нажатия кнопки «Пуск» (коммутация) двигатель приобретет нужную скорость не сразу. На разгон двигателя потребуется время.

Рассмотрим переходные процессы в цепи, содержащей последовательно соединенные резистор R и индуктивность L. Уравнение Кирхгофа для такой цепи

где u = u(t) - напряжение на входе цепи. Найдем решение этого уравнения для свободной составляющей тока, т.е. при u = 0, в виде iс = Iept. Для этого подставим выражение для тока в исходное уравнение и найдем значение p

Выражение Lp + R=0 представляет собой характеристическое уравнение, которое могло быть получено без подстановки общего выражения для свободной составляющей формальной заменой в однородном дифференциальном уравнении производных тока на pk, где k - порядок производной.

Таким образом, общее решение для тока при переходном процессе в R-L цепи можно представить в виде

где t = 1/|p| = L/R - постоянная времени переходного процесса; I - постоянная интегрирования, определяемая по начальным значениям; i - установившийся ток в цепи, определяемый по параметрам R и L и напряжению на входе u.

Длительность переходного процесса в цепи, определяемая значением t, возрастает с увеличением L и уменьшением R.

1. Смешанная RL и RC нагрузка в цепях переменного тока

1. Общий случай последовательного включения активных и реактивных сопротивлений.

Цепь с R, L и С представляет собой общий случай последо вательного соединения активных и реактивных сопро тивлений и является последовательным колебательным контуром (рис. 5,а). Принимаем фазу тока нулевой:

Построим векторную диаграмму при условии XL> Хс, т.е. UL = IXL> UC = IXC.

Вектор результирующего напряжения U замыкает многоугольник векторов UR, UL и UС (рис. 5,б). Вектор UL + Uc определяет напряжение на индуктив ности и емкости. Как видно из диаграммы, это напря жение может быть меньше напряжения на каждом из участков в отдельности. Это объясняется процес сом обмена энергией между индуктивностью и емкостью.

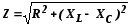
При XL> Xc реактивное сопротивление положительно и сопротивление цепи носит активно-индуктивный характер, при XL< Xc реактивное сопротивление отрицательно и сопротивление цепи носит активно-емкостной характер.

Таким образом, при XL≠XC преобладает или индуктивное, или емкостное сопротивление, т. е. с энергетической точки зрения цепь с R, L и С сводится к цепи с R, L или с R, С.

1. Переходные процессы в цепях с конденсатором. Включение RC цепи к источнику постоянного напряжения.
2. Законы Ома, Кирхгофа и их применение для расчета электрических цепей.
3. Активная, емкостная и индуктивная нагрузка в цепях переменного тока.
4. Расчет сложных электрических цепей методом контурных токов.