Алгоритм исследования функции
Нахождение области определения функции.
Определение 1. Область определения функции - множество, на котором задаётся функция.
Определение 2. Если задана функция, которая действует из одного множества в другое, то множество, из которого действует данная функция, называется областью определения.
Определение 3. Пусть задано отображение f, которое отображает множество X в Y, то есть: 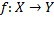 ; тогда
; тогда
множество X называется областью определения функции f и обозначается D(f), или dom f (от англ. domain «область»).
Правила нахождения области определения функции:
Пусть y=f(x) и y=g(x) - основные элементарные функции или их комбинации.
Для степенных функций вида 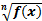 , где n - четное, область определения находится из системы:
, где n - четное, область определения находится из системы:
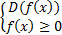
Для логарифмических функций вида 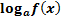 область определения находится из системы:
область определения находится из системы:
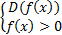
Для дробей вида 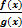 область определения находится из системы:
область определения находится из системы:
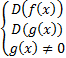
Для функций тангенса или котангенса вида tg(f(x)) или ctg(f(x)) область определения находится из систем соответственно:
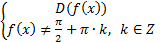 или
или 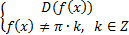
Для функций арксинус или арккосинус вида arcsin(f(x)) или arccos(f(x)) область определения находится из системы (т.к. областью определения арксинуса и арккосинуса является отрезок от -1 до 1):
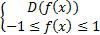

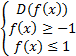
Для показательно степенных функций вида вида 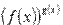 область определения находится из системы:
область определения находится из системы:
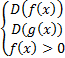
Область определения суммы (разности) функций вида 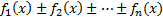 находится из системы:
находится из системы:
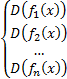
Область определения комбинации рассмотренных выше функций вида 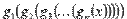 находится из системы:
находится из системы:
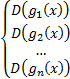
Нужно найти нули знаменателя и исключить их из области действительных чисел.
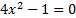
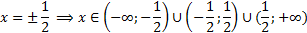
|
Исследование поведения функции на границе области определения, нахождение вертикальных асимптот.
Определение 4. На границах области определения функция имеет вертикальные асимптоты, если односторонние пределы функции в этих граничных точках бесконечны.
В нашем примере граничными точками области определения являются 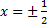 .
Исследуем поведение функции при приближении к этим точкам слева и справа, для чего найдем односторонние пределы: .
Исследуем поведение функции при приближении к этим точкам слева и справа, для чего найдем односторонние пределы:
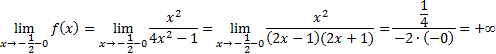
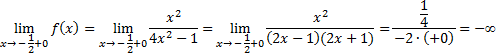
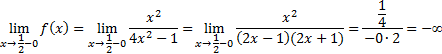
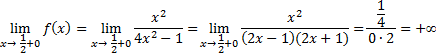 Так как односторонние пределы бесконечны, то прямые
Так как односторонние пределы бесконечны, то прямые 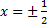 являются вертикальными асимптотами графика. являются вертикальными асимптотами графика.
|
Исследование функции на четность или нечетность.
Определение 5. Функция является четной, если y(-x)=y(x). Четность функции указывает на симметрию графика относительно оси ординат.
Определение 6. Функция является нечетной, если y(-x)= - y(x). Нечетность функции указывает на симметрию графика относительно начала координат.
Определение 7. Если ни одно из равенств (y(-x)=y(x), y(-x)= - y(x)) не выполняется, то функция является функцией общего вида.
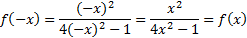 В нашем примере выполняется равенство y(-x)=y(x), следовательно, наша функция четная. Будем учитывать это при построении графика - он будет симметричен относительно оси Oy.
В нашем примере выполняется равенство y(-x)=y(x), следовательно, наша функция четная. Будем учитывать это при построении графика - он будет симметричен относительно оси Oy.
|
Нахождение промежутков возрастания и убывания функции, точек экстремума.
Промежутки возрастания и убывания являются решениями неравенств 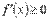 и
и 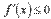 соответственно.
соответственно.
Определение 8. Точки, в которых производная обращается в ноль, называют стационарными.
Определение 9. Критическими точками функции называют внутренние точки области определения, в которых производная функции равна нулю или не существует.
Таким образом, чтобы определить промежутки возрастания и убывания функции:
1) находим производную;
2) находим критические точки;
3) разбиваем область определения критическими точками на интервалы;
4) определяем знак производной на каждом из промежутков. Знак «плюс» будет соответствовать промежутку возрастания, знак «минус» - промежутку убывания.
Определение 10. Точками экстремума функции являются точки, в которых функция определена, и, проходя через которые, производная меняет знак.
Находим производную на области определения:
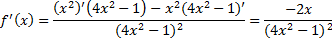 Находим критические точки:
1) находим стационарные точки (они же нули числителя): в нашем примере x=0;
2) находим нули знаменателя:
Находим критические точки:
1) находим стационарные точки (они же нули числителя): в нашем примере x=0;
2) находим нули знаменателя: 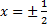 .
Наносим эти точки на числовую ось и определяем знак производной внутри каждого полученного промежутка. Можно взять любую точку из промежутка и вычислить значение производной в этой точке. Если значение положительное, то ставим «+» над этим промежутком и переходим к следующему, если отрицательное, то ставим «-» и т.д. К примеру, .
Наносим эти точки на числовую ось и определяем знак производной внутри каждого полученного промежутка. Можно взять любую точку из промежутка и вычислить значение производной в этой точке. Если значение положительное, то ставим «+» над этим промежутком и переходим к следующему, если отрицательное, то ставим «-» и т.д. К примеру, 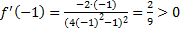 , следовательно, над первым слева интервалом ставим «+». , следовательно, над первым слева интервалом ставим «+».
 Схематично плюсами/минусами отмечены промежутки где производная положительна/отрицательна. Возрастающие/убывающие стрелочки показывают направление возрастания/убывания.
Делаем вывод:
- функция возрастает на промежутке
Схематично плюсами/минусами отмечены промежутки где производная положительна/отрицательна. Возрастающие/убывающие стрелочки показывают направление возрастания/убывания.
Делаем вывод:
- функция возрастает на промежутке  и на промежутке и на промежутке 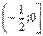 ;
- функция убывает на промежутке ;
- функция убывает на промежутке 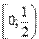 и на промежутке и на промежутке 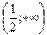 .
В нашем примере точкой экстремума является точка х=0. Значение функции в этой точке равно .
В нашем примере точкой экстремума является точка х=0. Значение функции в этой точке равно 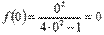 .
Так как производная меняет знак с «+» на «-» при прохождении через точку х=0, то (0; 0) является точкой локального максимума (если бы производная меняла знак с «-» на «+», то мы имели бы точку локального минимума). .
Так как производная меняет знак с «+» на «-» при прохождении через точку х=0, то (0; 0) является точкой локального максимума (если бы производная меняла знак с «-» на «+», то мы имели бы точку локального минимума).
|