РАДИАЛЬНО- СФЕРИЧЕСКИЙ ФИЛЬТРАЦИОННЫЙ ПОТОК
Фильтрационный поток называется радиально - сферическим, когда прямолинейные пространственные траектории частиц жидкости являются радиально сходящимися в центре одной сферы.
Примером радиально - сферического фильтрационного потока является приток жидкости к скважине, вскрывающей однородный пласт неограниченной толщины у его непроницаемой кровли через полусферический забой, радиус которого равен радиусу скважины (рис.15).
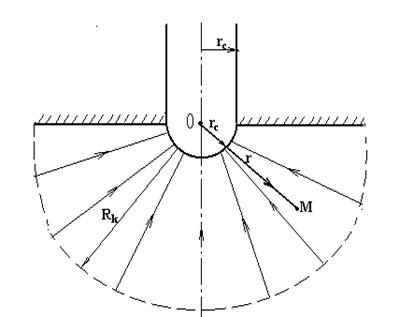
Рис.15
Рис.16
В этом случае давление и скорость фильтрации в любой точке фильтрационного потока будут функцией только расстояния r этой точки от центра забоя скважины; следовательно, этот вид фильтрационного потока также является одномерным.
Пусть начальное приведенное давление в пласте и на забое скважины равно Рк. Затем на забое давление снизилось до значения Рс = const. Приведенное давление на достаточно удаленной полусферической границе радиуса Rk сохраняется постоянным и равным Rk. В пласте будет иметь место установившийся радиально- сферический фильтрационный поток, описываемый дифференциальным уравнением (3.3).
Для упрощения исследования уравнение Лапласса (3.3) представим в сферических координатах, имея в виду, что Р = Р(r). Для этого рассмотрим трубку тока с телесным углом j и площадью фильтрационной поверхности w(S) = jr2 (рис.16). Используя равенства: S = Rk - r; dS = -dr и закон Дарси, получаем
;
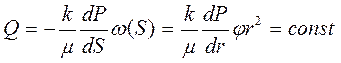поэтому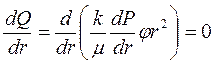 
,
откуда имеем:
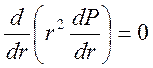. (3.32)
Уравнение (3.32) записываем в развернутом виде
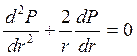. (3.33)
Уравнение (3.33) и есть дифференциальное уравнение Лапласса для радиально- сферического фильтрационного потока.
Дважды последовательно интегрируя уравнение (3.32), находим его общее решение
|
|
. (3.34)
Постоянные интегрирования С1 и С2 находим по граничным условиям:
при r =rc P = Pc = const;
при r = R P = Pk = const. (3.35)
Имеем:
;
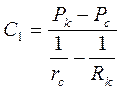. (3.36)
Тогда распределение давления Р=Р(r)получаем из общего решения (3.34) с учетом (3.36)
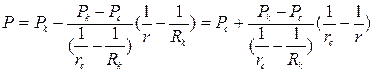. (3.37)
Как видно из (3.37) имеем гиперболический закон распределения приведенного давления Р = Р(r); уравнениями семейства равного приведенного давления (равного напора) являются концентрические полусферы (r = сonst).
Градиент приведенного давления определяем из выражения (3.34) на основании (3.36)
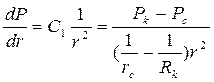. (3.38)
Используя (3.38), находим выражение для дебита добывающей скважины радиусом rc.
Q=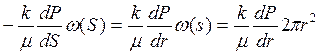 
,
то есть
. (3.39)
Как видно из (3.39) зависимость Q = Q(DPc) линейная, как и в случае плоскорадиального потока.
Находим выражение скорости фильтрации на расстоянии r от забоя скважины
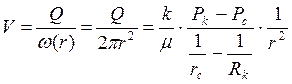, (3.40)
то есть скорость фильтрации V и градиент давления dP/dr в любой точке пласта обратно пропорциональны квадрату расстояния r этой точки до забоя скважины, поэтому график функции dP/dr от r будет более крутым в сравнении с плоскорадиальным потоком.
Аналогичным образом находим закон движения частиц жидкости по траектории.
;
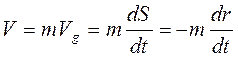или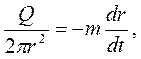 
.
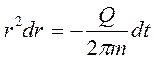Интегрируя в пределах (0 ¸ t) и (R0 ¸ r), получаем:
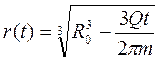. (3.41)
Плоскорадиальный фильтрационный поток
несжимаемой жидкости при нелинейных законах фильтрации
Рассмотрим плоскорадиальный фильтрационный поток несжимаемой жидкости при больших скоростях, когда становятся значительными инерционные составляющие гидравлического сопротивления и линейный закон Дарси нарушается. Для учета инерционных эффектов будем пользоваться степенной (1.25) и двучленной (1.22) зависимостями скорости фильтрации от градиента давления.
|
|
Степенной закон фильтрации в условиях плоскорадиального движения имеет вид
; 
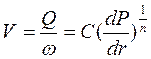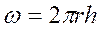. (3.42)
Для определения дебита скважины разделим переменные в (3.42) и проинтегрируем
;
;
,
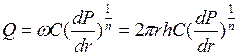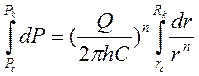Откуда
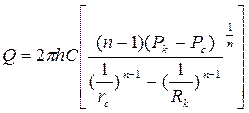. (3.43)
Распределение давления в пласте также определим из уравнения (3.42), проинтегрировав в других пределах:
; 
,
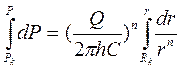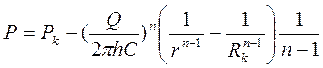или с учетом (3.43)
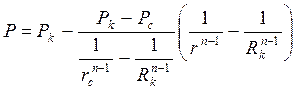. (3.44)
Градиент давления находим по формулам (3.42) и (3.43)
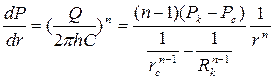. (3.45)
Скорость фильтрации определим из (3.42) с учетом (3.45).
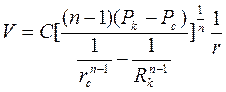. (3.46)
На основании полученных решений (3.43)-(3.46) для значений 1 < n < 2, находим фильтрационные характеристики потока для предельного случая n = 2, т.е. для случая закона Краснопольского(1.24):
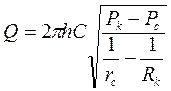. (3.47)
Пренебрегая в полученном равенстве величиной 
, получим
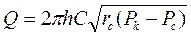; (3.48)
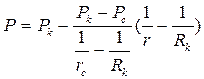, (3.49)
что совпадает с законом распределения давления Р(r) при радиально- сферическом потоке (3.37) по линейному закону фильтрации.
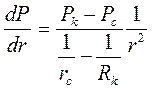, (3.50)
что также совпадает с аналогичной формулой для радиально- сферического потока при линейном законе фильтрации (3.38).
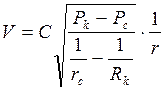. (3.51)
Проанализируем полученные формулы.
Как видно из формулы (3.43) для дебита скважины, индикаторная линия Q = Q(DPc) при 1 < n < 2 имеет вид выпуклой (к оси дебитов) степенной кривой с дробным показателем степени n < 2 (рис 17). В случае закона Краснопольского, как видно из формулы (3.48), индикаторная линия является параболой второго порядка, а при линейном законе фильтрации (n = 1) - прямая линия.
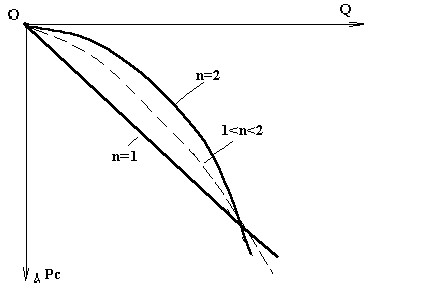
Рис.17
Кривая распределения давления Р (r) при нелинейном законе фильтрации (3.49) имеет формулу гиперболы, следовательно, воронка депрессии будет гиперболоидом вращения; крутизна воронки депрессии у стенки скважины будет больше, чем у логарифмической кривой (3.24) при линейном законе фильтрации.
|
|
Изменение скорости фильтрации вдоль линии тока V (r) подчиняется гиперболическому закону, как при нелинейной фильтрации (3.51), так и при линейной (3.26).
Следует отметить, что в реальных условиях нельзя считать, что во всем пласте - от контура питания до стенки скважины - справедлив единый нелинейный закон фильтрации с постоянным значением показателя степени n. Нарушение линейного закона фильтрации начинается, прежде всего, вблизи забоя скважины, в то время как в остальной части фильтрационного потока может сохраняться закон Дарси. По мере увеличения дебита скважины область с нелинейной фильтрацией будет расширяться. Поэтому в этих случаях необходимо пользоваться двучленной формулой (законом) фильтрации (1.22), которая для плоскорадиального потока имеет вид
, (3.52)
где
.
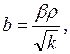
Выражая скорость фильтрации через дебит
,
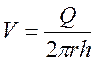перепишем (3.52) в виде
,
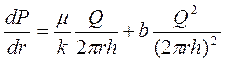откуда, разделяя переменные, получим
.
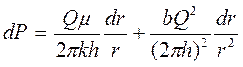Интегрируя последнее уравнение в пределах от r до Rk, от P до Pk и от rc до Rк, от Pc до Рк, находим соответственно:
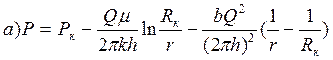; (3.53)
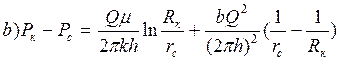. (3.54)
Из (3.54) дебит Q находится как положительный корень квадратного уравнения, из которого видно, что индикаторная линия
Q = Q (DРс) в этом случае является параболой.
По предложению Е.М.Минского уравнение (3.54) удобно представить в виде
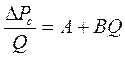, (3.55)
где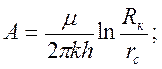 
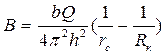. (3.56)
Тогда индикаторная диаграмма представляется прямой линией в координатах 
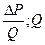(рис.18).
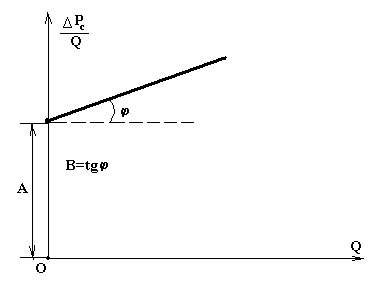
Рис.18
Построив промысловым методом индикаторную диаграмму (рис.18), находим параметры А = ОМ и В = tg j для последующего нахождения фильтрационных характеристик продуктивного пласта из выражений (3.56).