Практические расчеты по приведенным выше формулам (4.17) и (4.20) могут быть значительно упрощены, если использовать так называемый метод эквивалентных фильтрационных сопротивлений, предложенный Ю.П. Борисовым. Сущность метода состоит в замене полного фильтрационного сопротивления реального потока жидкости сложной конфигурации несколькими эквивалентными (равнозначными) последовательными или параллельными фильтрационными сопротивлениями простейших потоков (прямолинейно-параллельных и плоскорадиальных).
В основу метода ЭФС принят принцип электрогидродинамической аналогии (ЭГДА), согласно которому сила тока I соответствует расходу жидкости (дебиту Q), разность напряжений DU - разности давлений (депрессии DР), электрическое сопротивление проводника RЭЛ - фильтрационному сопротивлению пласта RФ. Принцип ЭГДА легко доказывается из сопоставления закона Ома (I=DU/R) с выражениями дебитов прямолинейной галереи (3.15) и одиночной скважины (3.27), определяемых по закону Дарси:
; (4.22)
, (4.23)
где 
- фильтрационное сопротивление в полосообразном пласте (рис.6);
- фильтрационное сопротивление в круговом пласте (рис.9).
Аналогично выражениям (4.22) и (4.23) преобразуем расчетные формулы (4.17) и (4.20).
Дебит одной скважины в прямолинейной бесконечной батарее скважин (рис. 24) можно записать
, (4.24)
где 
; 
.
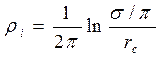Первое слагаемое re в знаменателе (4.24), как нетрудно заметить из сопоставления с формулой (4.22), равно фильтрационному сопротивлению в полосообразном пласте на участке длиной L от контура пласта до галереи. Площадь поперечного сечения пласта, приходящегося на данную скважину из ряда, равна произведению толщины пласта h =1 на ширину 2s, равную расстоянию между скважинами.
|
|
Второе слагаемое ri равно фильтрационному сопротивлению в круговом пласте (4.23) с радиусом контура питания RK = s/p.
Таким образом, сложный фильтрационный поток можно разбить на два простейших: прямолинейно-параллельный поток от контура пласта до галереи (прямолинейной цепочке скважин) и плоскорадиальный поток внутри галереи в круговом пласте с длиной контура 2pRK =2s, т.е. RK = s/p. Величину re принято называть внешним фильтрационным сопротивлением (на внешнем пути от контура до галереи), а ri – внутренним фильтрационным сопротивлением (внутри галереи), которое учитывает увеличение сопротивления притоку жидкости в скважину по сравнению с галереей длиной 2s. Сумма сопротивлений в (4.24) указывает на их последовательное соединение (рис.27).
 |
|
Дебит одной скважины в кольцевой батарее (рис.26) можно записать
, (4.25)
где 
,
.
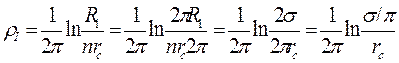Первое слагаемое rе в знаменателе выражения (4.25) представляет собой внешнее фильтрационное сопротивление части кругового пласта (сектора с углом a = 2s/R1 радиан) от контура до круговой галереи длиной 2s и радиусом R1 (рис.26), а второе слагаемое ri - внутреннее фильтрационное сопротивление притоку к скважине внутри галереи в круговом пласте с длиной контура 2pRK = 2s, т.е. RK = s/p. В данном случае сложный поток к одной скважине круговой батареи можно разбить на плоско-радиальный поток от контура питания до круговой галереи и плоско-радиальный поток к скважине внутри галереи.
Найдем суммарный дебит всей прямолинейной батареи скважин (рис.24)
|
|
, (4.26)
или
,
где 
; В=2sn – длина галереи.
–представляет собой внешнее суммарное фильтрационное сопротивление потоку жидкости от контура питания до галереи длиной В=2sn, расположенной на расстоянии L от контура питания.
;
– выражает внутреннее суммарное фильтрационное сопротивление, возникающее при подходе жидкости к скважине в зоне радиуса r=s/p, где фильтрация практически плоско-радиальная.
Найдем суммарный дебит для круговой батареи скважин (рис. 26).
, (4.27)
или
,
где
- внешнее суммарное фильтрационное сопротивление;
- внутреннее суммарное фильтрационное сопротивление.
Из расчетных формул (4.26) и (4.27) следует, что приток жидкости ко всем скважинам можно рассматривать как параллельное соединение проводников с одинаковыми сопротивлениями (
). Таким образом, фильтрационный поток к скважинам можно представить эквивалентной схемой электрических сопротивлений и для расчета использовать законы Ома и Кирхгофа (первый и второй законы), подразумевая в соответствии с принципом ЭГДА под силой тока, разностью напряжений и электрическими сопротивлениями их аналоги – расход жидкости, перепад давлений, фильтрационные сопротивления.
 |
Применительно к многорядной системе скважин пласт также представляется простой геометрической формой – прямолинейной или круговой. Реальный поток между скважинами соседних рядов заменяется фильтрацией между «проницаемыми» галереями с внутренними фильтрационными сопротивлениями скважин внутри галерей, дополняющими внешние фильтрационные сопротивления между галереями. Тогда представляя фильтрационную схему пласта эквивалентной ей электрической схемой сопротивлений и применяя к последней законы Ома и Кирхгофа, составляют уравнения интерференции рядов скважин для расчета дебитов или забойных давлений.
|
|
Схема эквивалентного фильтрационного сопротивления для полосообразной залежи
; 
; 
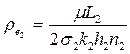; и т.д.
; 
; 
.
Схема эквивалентного фильтрационного сопротивления для круговой залежи.
; 
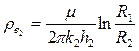и т.д.
; 
и т.д. 