· С веществом фиксированной массы провели опыт, в ходе которого к нему равномерно подводили теплоту. На рисунке представлен график зависимости температуры вещества T от времени наблюдения t за ним.

В начальный момент времени вещество находилось в кристаллическом состоянии (точка A). Опираясь на данные графика, определите, через сколько минут после начала эксперимента расплавилось 30% вещества? Ответ выразите в минутах, округлив до целых. Тепловыми потерями можно пренебречь.
Подсказка: все время плавления = 10 клеткам, значит 30% вещества соответствует 3 клеткам.
Находим, что всего от начала наблюдения 3 клетки (нагревание)+3 клетки (плавление). Значит, всего 6 клеток.
Всего время наблюдения 60 минут – 20 клеток. Тогда 1 клетка – 3 минуты.
Тогда нужное время = 18 минут.
3. С помощью весов мистер Фокс измерил массу одного листа из этой упаковки. Затем он загрузил этот лист в принтер и напечатал на каждой из двух его сторон по 2772 символов текста. Взвешивание этого листа с текстом показало, что его масса увеличилась на 1%. Исходя из этих данных, а также данных, приведённых на рисунке, определите, какова средняя масса одного символа напечатанного текста? Ответ выразите в мкг мкг, округлив до целых. Считать, что весы показывают точное значение массы.

Подсказка:
1. Масса листа = S* p (плотность) – эта характеристика указывает массу одного листа площадью 1 м2 (единица измерения - г/м2):
0.21 м * 0,297 м * 80 г/м² = 4,9896 г = 4989600 мкг
2. Масса отпечатанного текста увеличилась на 1%, то есть стала 101%, тогда:
1.01 * 4989600 мкг = 5039496 мкг
3. масса всех символов равна разности масс с текстом и без текста, то есть 49896 мкг
4. всего символов с двух сторон: 2* 2772 = 5544
5. средняя масса одного символа равна: 49896 мкг/5544 = 9мкг
4. Пять склеенных деревянных кубиков плотностью ρ склеили с фторопластовым кубиком массой m=70 г в единое тело так, как показано на рисунке.
Найдите массу получившегося тела, если его средняя плотность оказалась равной 1,3ρ. Ответ выразите в г, округлив до целых. Все шесть кубиков являются сплошными и имеют одинаковые геометрические размеры. Массой клея пренебречь.

Подсказка: среднюю плотность тела, массу всех кубиков разделить на общий объем.
Общая масса всего тела: 5m +70
Общий объем: 6V, V=m/ ρ
Тогда 
Тогда масса получившегося тела равна 25*5+70=220г
6. На дне мензурки, наполненной водой, лежал металлический стержень в форме прямоугольного параллелепипеда. Его вынули, в результате чего уровень воды в мензурке понизился так, как показано на рисунке.
Определите высоту стержня, если известно, что его можно мысленно разделить на три одинаковых кубика. Ответ выразите в миллиметрах, округлив до целых.


8. На весах стоит мензурка, частично наполненная водой. Над ней с помощью тонкой нити удерживают частично погруженный в воду чугунный шарик так, как показано на рисунке слева. После того, как нить отпустили, шарик утонул и оказался на дне мензурки так, как показано на рисунке справа.
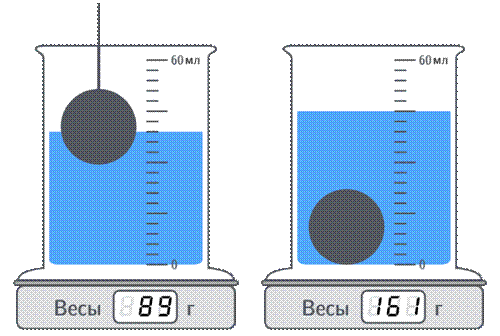
Опираясь на эти данные, определите объём шарика. Ответ выразите в млмл, округлив до целых. Плотность чугуна составляет гсмρ=7 г/см3, а воды – гсмρ0=1 г/см3.
Подсказка: обозначим
первоначальный объем воды V0,
объем шара V
объем погруженной части шара в первом опыте Vx.
по показаниям мензурок V1=V0+Vx, V2=V0+V, отсюда V=(V2-V1)+Vx=Vx+6
цена деления шкалы мензурки 60/5*4=3см^3).
обозначим массу воды m0, плотность воды r1 и плотность чугуна r2.
тогда по показаниям весов m1=m0+r1Vx, m2=m0+r2V, отсюда Vx=[r2V-(m1-m2)]/r1=7V-72. подставляем это в найденное прежде V=Vx+6,
получаем 6V=66 и V=11см^3.