ЗАДАНИЕ НА ЛАБОРАТОРНУЮ РАБОТУ № 2
«ВЕКТОРА И МАТРИЦЫ»
1. 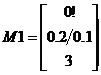

Упростить матрицы М1 и М2.
Составить новые матрицы М12 и М21, причем:
1) М12 = М1 рядом с М2;
2) М21 = М2 рядом с М1.
2. Заданы матрицы: 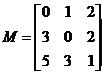
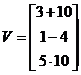
1) Найти матрицу W = 2V;
2) Найти сумму элементов V;
3) Найти определитель матрицы М;
4) Найти скалярное и векторное произведение V и W;
5) Найти матрицу, обратную М;
6) Найти транспонированную W;
7) Найти произведение прямой и обратной матриц М;
3. Заданы матрицы: 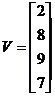

Используя стандартные функции, найти:
1) Диагональную матрицу V;
2) Число строк и столбцов М;
3) Число элементов в V, индекс последнего элемента V.
4. 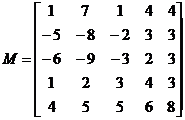
При помощи функции submatrix извлечь элементы матрицы, расположенные между строками 1 и 2 и между столбцами 0 и 2 (включительно). При помощи этой же функции переставить в полученной матрице: а) столбцы; б) строки.
5. 
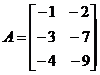
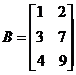
Объединить матрицы: 1) В под А; 2) А рядом с М.
ВЕКТОРНЫЕ И МАТРИЧНЫЕ ОПЕРАТОРЫ
| Операция | Обозн. | Клав. | Описание |
| Умножение матрицы на скаляр | A∙z | * | Умножает каждый элемент А на скаляр z. |
| Скалярное произведение | u∙v | * | Возвращает скаляр: ∑ui∙vi. Векторы должны иметь одинаковое число элементов. |
| Матричное умножение | A∙B | * | Возвращает произведение матриц А и В, число столбцов А должно соответствовать числу строк в В. |
| Умножение матрицы на вектор | A∙v | * | Возвращает произведение матриц А и v, число столбцов А должно соответствовать числу строк v. |
| Деление | 
| / | Делит каждый элемент массива на скаляр z. |
| Сложение векторов и матриц | A+B | + | Складывает соответствующие элементы А и В, массивы А и В должны иметь одинаковое число строк и столбцов. |
| Скалярная сумма | A+z | + | Добавляет z к каждому элементу А. |
| Векторное и матричное вычитание | A-B | - | Вычитает соответствующие элементы массива А из элементов массива В, массивы А и В должны иметь одинаковые размеры. |
| Скалярное вычитание | A-z | - | Вычитает z из каждого элемента А. |
| Изменение знака | -A | - | Умножает все элементы А на -1. |
| Степени матрицы, обращение матриц | Mn | ^ | n-ная степень квадратной матрицы М. n должно быть целым числом. М-1 представляет матрицу, обратную к М, другие отрицательные степени – степени обратной матрицы. |
| Длина вектора | 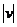
| | | Возвращает 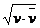 , где , где  - вектор, комплексо сопряженный к v. - вектор, комплексо сопряженный к v.
|
| Детерминант | 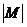
| | | Возвращает детерминант квадратной матрицы М. Результат – скаляр. |
| Транспонирование | AT | Ctrl+1 | Возвращает матрицу, в которой строки – столбцы А, а столбцы – строки А. А может быть вектором или матрицей. |
| Векторное произведение | 
| Ctrl+8 | Возвращает векторное произведение для векторов с тремя элементами u и v. |
| Комплексное сопряжение | 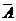
| “ | Меняет знак мнимой части каждого элемента А. |
| Суммирование элементов | ∑ | Ctrl+4 | Суммирует элементы вектора v. Возвращает скаляр. |
| Векторизация | 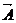
| Ctrl+- | Предписывает в выражении с А производить операции поэлементно. |
| Верхний индекс | A<n> | Ctrl+6 | Извлекает n-ный столбец массива А. Возвращает вектор. |
| Нижний индекс вектора | vn | [ | n-ный элемент вектора. |
| Нижние индексы матрицы | Am,n | [ | Элемент матрицы, находящийся в m-ом ряду и n-ой строке. |
ВЕКТОРНЫЕ И МАТРИЧНЫЕ ФУНКЦИИ
| Функция | Возвращается… |
| rows (A) | Число строк в массиве А. Если А – скаляр – возвращается 0. |
| cols (A) | Число столбцов в массиве А. Если А – скаляр – возвращается 0. |
| length (v) | Число элементов в векторе v. |
| last (v) | Индекс последнего элемента в векторе v. |
| max (A) | Самый большой элемент в массиве А. Если А имеет комплексные элементы, возвращает наибольшую вещественную часть плюс I, умноженную на наибольшую мнимую часть. |
| min (A) | Самый маленький элемент в массиве А. Если А имеет комплексные элементы, возвращает наименьшую вещественную часть плюс I, умноженную на наименьшую мнимую часть. |
| identity (n) | 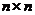 единичная матрица единичная матрица
|
| Re (A) | Массив, состоящий из элементов, которые являются вещественными частями элементов А. |
| Im (A) | Массив, состоящий из элементов, которые являются мнимыми частями элементов А. |
| diag (v) | Диагональная матрица, содержащая на диагонали элементы v. |
| geninv (A) | Левая обратная к А матрица L такая, что L∙A=I, где I – единичная матрица, имеющая то же самое число столбцов, что и А. Матрица А - 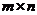 вещественная матрица, где m ≥ n. вещественная матрица, где m ≥ n.
|
| rref (A) | Ступенчатая форма матрицы. |
| tr (m) | Сумма диагональных элементов, называемая следом М. |
| augment (A,B) | Массив, сформированный расположением А и В бок о бок. Массивы А и В должны иметь одинаковое число строк |
| stack (A,B) | Массив, сформированный расположением А над В. Массивы А и В должны иметь одинаковое число столбцов. |
| submatrix (A,ir,jr,ic,jc) | Субматрица, состоящая из всех элементов, содержащихся в строках с ir по jr и столбцах с ic по jc. Чтобы поддерживать порядок строк и-или столбцов, удостоверьтесь, что ir ≤ jr и ic ≤ jc, иначе порядок строк и-или столбцов будет обращен. |
| eigenvals (M) | Вектор, содержащий собственные значения матрицы М. |
| eigenvec (M,z) | Матрица, содержащая нормированный собственный вектор, соответствующий собственному значению z квадратной матрицы М. |
| eigenvecs (M) | Матрица, содержащая нормированные собственные векторы, соответствующие собственным значениям квадратной матрицы М. n-ый столбец возвращенной матрицы – собственный вектор, соответствующий n-ному собственному значению, возвращенному eigenvals. |
Операция ORIGIN – начало массива. Определяет индекс первого элемента массива, т.е. если значение этой переменной равно нулю (по умолчанию), то первый элемент массива будет иметь индекс, равный нулю.