ОПТИМИЗАЦИЯ РАСКРОЯ ДРЕВЕСНОСТРУЖЕЧНЫХ ПЛИТ

 

2.1 Цель работы: изучение методики оптимизации раскроя древесностружечных плит.

 

2.2 Теоретическая часть

 

Область математики, занимающаяся исследованием и решением задач нахождения наибольших или наименьших значений функций на конечных (или счетных) множествах, называется дискретным программированием. Наиболее изученными задачами этого раздела являются целочисленные задачи линейного программирования, т.е. задачи линейного программирования, в которых на все переменные или на их часть наложено дополнительное требование целочисленности. Аналогичным образом определяются целочисленные задачи и для более общих задач оптимального программирования – можно говорить, например, о задачах выпуклого целочисленного программирования и т.д. От целочисленных задач принято отличать так называемые дискретные задачи математического программирования, в которых областью допустимого изменения переменных является не множество целых неотрицательных чисел, а некоторое произвольное конечное множество. Однако формально такие задачи могут быть сведены к целочисленным. Здесь будут рассматриваться лишь модели линейного целочисленного программирования.

В моделях линейного целочисленного программирования по сравнению с обычными моделями линейного программирования на все переменные величины или на некоторые из них налагается требование целочисленности. В первом случае обычно говорят о полностью целочисленных, а во втором - о частично целочисленных задачах.

Значительная часть задач экономического характера требует целочисленности решений. Различают две разновидности моделей задач линейного целочисленного программирования: задачи с неделимостью и задачи с булевыми переменными. К первым относятся модели задач, в которых искомые величины являются физически неделимыми объектами, как, например, число предприятий, число распределяемых машин, количество единиц неделимой информации и т.п. Модели с булевыми переменными (т.е. переменными, принимающими два значения "0" или "1") охватывают разнообразные оптимальные задачи комбинаторного характера, задачи с дополнительными логическими условиями, которые с помощью искусственно вводимых булевых переменных приводятся к линейным моделям задач целочисленного программирования.

Оптимальное решение, найденное симплексным методом, как правило, не является целочисленным. Округление полученных результатов до ближайших целых чисел допустимо в тех случаях, когда значения переменных, образующих оптимальный план исходной задачи, достаточно велики, и погрешностями округления с практической точки зрения можно пренебречь. Однако, во многих случаях такое округление дает вообще недопустимое решение, а если решение оказывается допустимым, то далеко не лучшим среди целочисленных решений, т.е. не оптимальным. Поэтому для нахождения оптимального целочисленного решения нужны особые методы и алгоритмы.

Методы целочисленной оптимизации можно разделить на три основные группы: методы отсечений, комбинаторные методы и приближенные методы. Название "методы отсечений" связано с тем обстоятельством, что в систему ограничений вводятся дополнительные неравенства, отсекающие некоторые части множества допустимых решений, в которых отсутствуют точки с целочисленными координатами. Комбинаторные методы занимают доминирующее положение в целочисленном программировании. Это методы направленного частичного перебора допустимых решений. Наиболее известным комбинаторным методом является метод ветвей и границ, в котором из рассматриваемой задачи получается две подзадачи путем специального разбиения множества допустимых решений и отбрасывания областей, не содержащих целочисленных решений. Трудности машинной реализации точных методов решения задач целочисленного программирования привели к появлению приближенных методов случайного поиска в сочетании с локальной оптимизацией, а также методов, построенных на использовании особенностей конкретной задачи.

Среди задач целочисленной оптимизации исключительно важными для практики являются, так называемые, раскройные задачи. В этих задачах требуется наилучшим образом произвести раскрой каких-либо материалов. Это могут быть бревна, брус, прутья, арматура и другие одномерные материалы. Раскрой может быть двумерный или плоский, если требуется раскроить плиты (древесно-стружечные, древесно-волокнистые и пр.), фанеру, стекло, линолеум и другие материалы. Моделирование оптимального раскроя материалов является одним из способов эффективного использования производственных ресурсов предприятия.

 

2.3 Пример выполнения работы

 

Решим задачу плоского раскроя при следующих исходных данных. Древесно-стружечные плиты имеют размер 230см. х 120см., и их необходимо раскроить на детали вида I размером 170см. х 50см. в количестве 89 штук и детали вида II размером 110см. х 65см. в количестве 45 штук. Найти оптимальный план раскроя по трем критериям оптимальности, указанным в задании на контрольную работу.

 

2.3.1 Карты раскроя

 

Возможные варианты (или карты) раскроя древесно-стружечных плит на требуемые детали изобразим на рисунке 2.1.

 

Рисунок 2.1 - Карты раскроя ДСП

 

В таблице 2.1 приведены возможные способы раскроя плит, количество деталей двух типов, полученных от каждого способа раскроя, и потребности в этих деталях.

 

Таблица 2.1 – Возможные способы раскроя плит

 

Детали вида	Способы (карты) раскроя	Потребности в деталях
I II
Число раскраиваемых плит

 

2.3.2. Система ограничений

Введем обозначения. Пусть

– количество плит, которые должны быть раскроены по первой карте;

– количество плит, которые должны быть раскроены по второй карте;

– количество плит, которые должны быть раскроены по третьей карте.

На основе данных таблицы 2.1 получим систему ограничений на требуемое количество деталей. Деталей вида I будет получено штук, а деталей вида II будет получено штук. Поэтому должна выполняться система неравенств

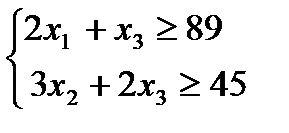. (2.2)

 

Поскольку число раскроенных плит должно быть целым, то условия неотрицательности и целочисленности неизвестных

 

(2.2)

 

очевидны. Условия (2.1)-(2.2) представляют собой систему ограничений раскройной задачи.

2.3.3. Критерий минимизации затраченных плит

Общее число затраченных плит равно сумме числа плит, раскроенных по всем картам. Поэтому из определения функции следует, что

 

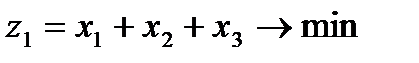. (2.3)

 

Решение в Excel.

2.3.4. Критерий минимизации площадей отходов

Определив площадь отходов для каждого варианта раскроя одного листа ДСП, получим м², м², м². Тогда для второго критерия оптимальности целевая функция имеет вид

 

. (2.4)

 

2.3.5. Критерий минимизации суммарной длины пропилов

Длины пропилов для каждого варианта раскроя листа ДСП соответственно равны: м, м, м. Поэтому целевая функция для третьего критерия оптимальности оказывается равной

 

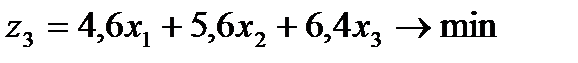. (2.5)

 

Системы ограничений (2.1)-(2.2) при этом остаются без изменения. Таким образом, новые модели отличаются от модели (2.1) –(2.3) только целевыми функциями.

 

 

2.3.6. Решение в Excel

Решение всех трех задач оптимизации, полученное в Excel, приведено в таблицах 2.2 – 2.4, размещенных на трех листах Excel. Заполнение данных на всех трех листах следующее:

· помещается пояснительная информация, выделенная серым цветом,

· ячейки B4: D4 остаются пустыми,

· в блоке ячеек B7: D8 записываются коэффициенты системы ограничений (10),

· в ячейках E7: E8 записываются формулы для левых частей системы ограничений,

· в ячейках G7: G8 помещаются правые части системы ограничений,

· в блоке ячеек B10: D12 помещаются коэффициены целевых функций (2.3) – (2.5), а в ячейках E10: E12 – формулы для вычисления значений целевых функций.

Отличие состоит только в указании целевых ячеек при обращении к процедуре «Поиск решения». На листе 1 целевой ячейкой служит E10 (таблица 2.2), на листе 2 – ячейка E11 (таблица 2.3), на листе 3 – ячейка E12 (таблица 2.4). Эти ячейки отмечены справа символом *.

 

Таблица 2.2 - Целевая функция 1 – общее количество плит

 

	A	B	C	D	E	F	G
	Целевая функция 1 – общее количество плит
	Число плит	x1	x2	x3
	Значение
					Ограничения
					Левая часть	Знак	Правая часть
	Детали вида I					>=
	Детали вида II					>=
					ЦФ
	z1, шт					*
	z2, м2	1,06	0,615	0,48	46,02
	z3, м	4,6	5,6	6,4

 

 

Таблица 2.3 - Целевая функция 2 – общая площадь отходов

 

	A	B	C	D	E	F	G
	Целевая функция 2 – общая площадь отходов
	Число плит	x1	x2	x3
	Значение
					Ограничения
					Левая часть	Знак	Правая часть
	Детали вида I					>=
	Детали вида II					>=
					ЦФ
	z1, шт
	z2, м2	1,06	0,615	0,48	42,72	*
	z3, м	4,6	5,6	6,4	569,6

 

Таблица 2.4 - Целевая функция 3 – общая длина пропилов

 

	A	B	C	D	E	F	G
	Целевая функция 3 – общая длина пропилов
	Число плит	x1	x2	x3
	Значение
					Ограничения
					Левая часть	Знак	Правая часть
	Детали вида I					>=
	Детали вида II					>=
					ЦФ
	z1, шт
	z2, м2	1,06	0,615	0,48	56,925
	z3, м	4,6	5,6	6,4		*

 

2.3.7. Сравнение результатов оптимизации для различных критериев

Результаты решения, полученные выше, сведены в таблице 2.5. Их можно поместить в Excel на лист 4.

 

Таблица 2.5 – Результаты полученных решений

 

Критерий оптимальности (на минимум)	Число раскроенных плит	Значения критерия
Карта 1	Карта 2	Карта 3
Расход плит					46,02
Площадь отходов					42,72	569,6
Длина пропилов					56,925

 

Как следует из таблицы 2.5, наблюдается значительное различие между полученными оптимальными планами для различных критериев оптимальности. Так, например, для второго критерия расход плит может быть превышен по сравнению с оптимальным вариантом более, чем на .

В рассмотренной задаче отсутствует единственный признак оптимальности, и имеет место «неопределенность» цели.

На рисунке 2.2. представлена пространственная диаграмма, характеризующая результаты оптимизации по трем критериям. Она строится на основе данных таблицы 2.5. Для каждого критерия (им соответствуют строки) на диаграмме изображено количество плит, которое должно быть раскроено по всем картам (им соответствуют столбцы).

 

Рисунок 2.2 - Отображение результатов оптимизации на диаграмме

 

 

2.3 Техническое обеспечение

 

2.3.1 Компьютеры и выход в сеть интернета.

 

2.4 Содержание отчета

2.4.1 Отчет должен содержать следующие пункты:

· задание на работу с конкретными исходными данными студента (приложение 2),

· карты раскроя плиты на детали,

· математические модели, составленные для каждого критерия оптимальности,

· решение в Excel задач оптимизации для каждого критерия,

· сравнение полученных результатов оптимизации, выводы по работе.