Тема 5. ДИНАМИКА ЖИДКОСТЕЙ.
ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ
Наблюдается два вида течение жидкости (газа). В одних случаях жидкость как бы разделяется на слои, которые скользят друг относительно друга, не перемешиваясь. Такое течение называется л а м и н а р н ы м (слоистым). Если в ламинарный поток ввести подкрашенную струйку, то она сохраняется, не разрываясь, на всей длине потока, т.к. частицы жидкости в ламинарном потоке не переходят из одного слоя в другой. Ламинарное течение стационарно. При чем для него характерно то, что каждый слой движется с какой-то определенной скоростью υ. При небольших скоростях течения жидкости по трубе наблюдается ламинарное течение. Характер изменения скорости течения с расстоянием от оси трубы изображен на рис.4.7.
 Рис. 4.7 Рис.4.8
Рис. 4.7 Рис.4.8 


Ламинарное течение Турбулентное течение
При увеличении скорости потока характер течения существенно изменяется. Возникает энергичное перемешивание жидкости, в результате чего внутри жидкости появляются вихри - турбулентности. Такое течение называется ту р б у л е н т н ы м. «Профиль» скоростей внутри турбулентного потока изображен на рис.4.8. Очевидно, что при турбулентном течении скорость в каждой точке сечения трубы приобретает некое значение. И только вблизи стенок скорость изменяется, при чем гораздо сильнее, чем при ламинарном течении, но в остальной части сечения скорость изменяется меньше.
Рассмотрим некоторые законы, выполняющиеся в ламинарном потоке жидкости (газа).
ТЕЛО В ЛАМИНАРНОМ ПОТОКЕ
ДИНАМИЧЕСКАЯ ВЯЗКОСТЬ
Вследствие того, что ламинарный поток как бы расслаивается, и каждый слой движется с определенной скоростью, то в процессе движения между слоями возникает трение, которое применительно к жидкостям и газам называется внутренним трением.
|
|
Внутренне трение характеризуется коэффициентом, который называется динамической вязкостью.
Динамическая вязкость обозначается греческой буквой η («эта») и измеряется в системе СИ в Паскалях-секунда: [η]=Па·с.
Свойства динамической вязкости:
· Динамическая вязкость жидкостей резко уменьшается с повышением температуры жидкости;
· Динамическая вязкость газов наоборот резко увеличивается с повышением температуры газа.
Кроме динамической вязкости применяются понятия текучести и кинематической вязкости.
Текучестью φ («фи») называется величина, обратная динамической вязкости:  .
.
А кинематической вязкостью ν («ню») называется отношение динамической вязкости к плотности среды (жидкости или газа):  .
.
Единица измерения кинематической вязкости: [ν]= м2/с.
ЗАКОН СТОКСА
Стокс установил следующую закономерность: для тела, находящегося в ламинарном потоке, сила сопротивления среды пропорциональна коэффициенту динамической вязкости η, скорости ν движения тела относительно жидкости и характерному размеру тела l.
Если тело имеет сферическую форму, то сила сопротивления потока будет равна:
Fc=6πηrv.
где r – радиус тела,
υ – относительная скорость тела (потока).
Скорость считается относительно, т.к. она зависит от конкретных условий: если тело движется в покоящейся жидкости, то это скорость тела; если поток омывает зафиксированное тело, то это скорость потока; если тело движется в потоке, то это скорость тела относительно потока.
|
|
Как и любая другая сила трения, Fc всегда направлена в сторону противоположную движению тела.
Заметим, что на законе Стокса основано определение вязкости жидкости вискозиметром Гёпплера: в трубку определенногодиаметра, заполненную жидкостью, вязкость которой надо определить, опускают шарик и измеряют скорость его падения, которая и является мерой вязкости жидкости.
ТЕЛО В ТУРБУЛЕНТНОМ ПОТОКЕ
Когда скорость течения превысит определенное критическое значение, жидкость или газ начинают двигаться турбулентно. Возникают вихри, а следовательно, и силы, препятствующие течению. Сопротивление потоку, т.е. сила, действующая на помещенное в поток тело, складывается из разности давлений перед и за телом и силы трения на поверхности тела.
Сила гидравлического сопротивления, действующая на тело со стороны турбулентного потока, описывается формулой:
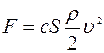 ,
,
где: с – коэффициент, зависящий от формы тела (безразмерное число, табличное
значение, определяется экспериментально и зависит от скорости);
S – площадь наибольшего сечения тела в плоскости, перпендикулярной направлению потока;
ρ – плотность текущей жидкости(газа);
υ – относительная скорость движения тела в среде.
Т.о. гидравлическое сопротивление увеличивается пропорционально квадрату скорости потока: F ~ υ2.
ЧИСЛО РЕЙНОЛЬДСА
Коэффициент с зависит не только от формы тела, но и от свойств среды, в которой происходит движение. Коэффициент с является функцией числа Рейнольдса Re:
|
|
 ,
,
где l – характерные размеры тела (для труб это, как правило диаметр);
ρ – плотность текущей среды;
υ – относительная скорость тела;
η – динамическая вязкость жидкости (газа);
ν – кинематическая вязкость жидкости (газа).
При малых Re течение любой жидкости (газа) будет ламинарным. Если скорость возрастает и достигает критического значения υкр (соответствующего Reкр), то ламинарное течение сменяется турбулентным.
Критическое число Рейнольдса для потока в гладких трубах: Reкр ≈ 1160.
Из формулы для Re следует, что число Рейнольдса не изменится, если уменьшить размеры тела и соответственно увеличить скорость потока или уменьшить вязкость среды. Таким образом, число Рейносльдса может служить критерием подобия для течения жидкостей в трубах, каналах и т.д.