Цель: формирование у обучающихся понятие относительной частоты случайного события; умения находить относительную частоту случайного события; развитие умения сравнивать, выявлять закономерности, обобщать.
1. Ответить на вопросы теста.
Тестовое задание
1. Какое из перечисленных событий достоверное?
С. Вода в реке Ока закипит.
В. Круглая отличница получит двойку.
Ч. В году найдётся месяц, в котором будет пять воскресных дней.
2. Какое из перечисленных событий невозможно?
А. В 12 часов ночи в городе идёт снег, а через 24 часа будет светить солнце.
О. Сорванный цветок погибнет.
М. Если до воздушного шарика дотронуться иголкой, то он лопнет.
3. Какое из данных событий случайное?
Р. Ударом молотка можно разбить стекло.
О. Воробей научится говорить.
С. Завтра будет хорошая погода.
4. Из перечисленных событий выберите более вероятное.
У. В мае в нашем городе пойдёт снег.
Т. На день рождения тебе подарят игрушку.
О. В выходной день вы просыпаетесь, а на улице уже темно.
5. Какое из следующих событий менее вероятное
Н. Ты купил мороженное и выбросил его в урну.
К. После четверга будет пятница.
О. Новая электрическая лампочка не загорится.
6. Из данных событий выберите то, которое является равновозможным (равновероятным). В коробке лежат 8 яблок и 5 лимонов.
А. Из коробки вынут апельсин или лимон.
Т. Вынутый предмет будет яблоком или лимоном.
М. Из коробки вынули апельсин или лимон.
7. На школьной олимпиаде по математике было предложено 5 заданий. Алёша выполнил 3,5 задания, а Игорь- 2 задания. У кого из ребят больше шансов стать победителем на школьной олимпиаде?
А. У Алёши. И. У Игоря.
Ответы закодированы буквами. Прочитаем, какое слово получается, если правильно ответить на все вопросы.
|
|
2. Сделать конспект.
Итак, сейчас мы разберемся, что такое частота события.
Люди давно заметили, что многие события происходят с той или иной, на удивление постоянной, частотой.
Начиная с ХVІІІ в. многие исследователи проводили серии испытаний с подбрасыванием монеты.
В таблице приведены результаты некоторых таких
| Исследователь | Количество подбрасываний монеты | Количество выпадений герба | Частота выпадения герба |
| Жорж Бюффон(1707–1788) | 0,5069 | ||
| Огастес де Морган (1806–1871) | 0,5005 | ||
| Уильям Джевонс(1835–1882) | 20 480 | 10 379 | 0,5068 |
| Всеволод Романовский (1879–1954) | 80 640 | 39 699 | 0,4923 |
| Карл Пирсон(1857–1936) | 24 000 | 12 012 | 0,5005 |
| Уильям Феллер (1906–1970) | 10 000 | 0,4979 |
По приведенным данным прослеживается четкая закономерность: при многократном подбрасывании монеты частота появления герба незначительно отклоняется от числа 0,5.Следовательно, можно считать, что вероятность события «выпадение герба» приблизительно равна 0,5. В каждом из рассмотренных примеров использовалось понятие частота случайного события. Эту величину мы вычисляли по формуле:
отношение числа испытаний, в которых это событие наступило, к числу всех возможных событий.
Далее по частоте мы оценивали вероятность события, а именно: вероятность случайного события приближенно равна частоте этого события, найденной при проведении большого количества испытаний (наблюдений).
Такую оценку вероятности случайного события называют статистической. Ее используют в разных областях деятельности человека: физике, химии, биологии, страховом бизнесе, социологии, экономике, здравоохранении, спорте.
|
|
Вводимые обозначения:
А – событие;
m – число испытаний, при которых произошло событие А;
n – общее число испытаний;
Р(A) =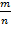 
– относительная частота случайного события.
Аксиомы Колмогорова:
1. 0£Р(A)£1 для любого события А
2. Р(A)=1, если событие А достоверно
3. Р(A+В)= Р(A)+ Р(В), если события А и В несовместны.
3. Разберем на примере.
Пример. Иван попал в мишень 3 раза, Петр – 4. Кто из них лучше стреляет?
Можно ответить, что Петр – лучше, так как больше число попаданий. Но мы не знаем, сколько у каждого было попыток. Например, Иван сделал всего три выстрела и попал все три раза, относительная частота попадания Р(A) = 3/3 = 1. А Петр сделал серию из 20 выстрелов и попал всего четыре раза: Р(A) =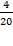 
= 0,2.
4. Решить задачи:
1. В партии из 1000 деталей отдел технического контроля обнаружил 12 нестандартных деталей. Какова относительная частота появления нестандартных деталей?
2. В 2006 г. в городе Дмитрове в июле и августе было 46 солнечных дней. Какова относительная частота солнечных дней в указанные два месяца?
5. Домашнее задание.
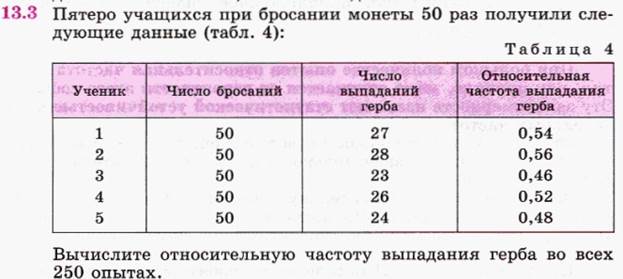
Выполненные задания присылать с указанием группы и фамилии
эл. почта: masha_fin@mail.ru