ЦИФРОВЫЕ И МИКРОПРОЦЕССОРНЫЕ УСТРОЙСТВА
Методические указания по выполнению курсового проекта
для студентов специальностей
2-45 01 03 – Сети телекоммуникаций
2-45 01 02 – Системы радиосвязи, радиовещания и телевидения
Минск
УДК 81.332
ББК 32.97
Ц75
Рекомендовано к изданию
кафедрой информатики и вычислительной техники
19 января 2011 г., протокол № 5
Составитель
В. И. Богородов, преподаватель высшей категории
кафедры информатики и вычислительной техники
Рецензент
Е. В. Новиков, доцент кафедры информатики и
вычислительной техники, канд. техн. наук
| Ц75 | Цифровые и микропроцессорные устройства: методические указания по выполнению курсового проекта для студентов специальностей 2-45 01 03 – Сети телекоммуникаций, 2-45 01 02 – Системы радиосвязи, радиовещания и телевидения / сост. В. И. Богородов. – Минск: УО ВГКС, 2011. – 68 с. ISBN 978-985-7002-15-3. Приводятся методические указания по выполнению курсового проекта по цифровой схемотехнике. Рассматриваются принципы построения умножителей, сумматоров и комбинационных программируемых сдвигателей. Предназначено для студентов и преподавателей колледжа. УДК 81.332 ББК 32.97 |
ISBN 978-985-7002-15-3 ©Учреждение образования
«Высший государственный
колледж связи», 2011
ВВЕДЕНИЕ
Курсовой проект по дисциплине «Цифровые и микропроцессорные устройства» выполняется студентами специальностей 2-45 01 03 – Сети телекоммуникаций, 2-45 01 02 – Системы радиосвязи, радиовещания и телевидения третьего курса дневной формы обучения и пятого курса заочной формы обучения.
Целью курсового проекта является формирование начальных умений и навыков самостоятельного проектирования цифровых устройств, углубление и расширение знаний функционирования типовых узлов цифровых устройств.
Задания к курсовому проекту имеют разный уровень сложности. Задания по темам № 1-3 предполагают разработку принципиальных электрических схем цифровых устройств на микросхемах схемотехники КМОП отечественного производства по заданной структурной электрической схеме (второй уровень). Задания по темам № 1-3 разработаны в десяти вариантах. Номер варианта студенты определяют по данным таблицы 1 (номер варианта может быть задан преподавателем индивидуально). Задания по теме № 4 (третий уровень) предполагают разработку структурной и принципиальной электрической схем цифрового устройства по заданным исходным данным. Задания по теме № 4 разработаны в пяти вариантах и выдаются преподавателем только индивидуально.
Курсовой проект должен состоять из трех листов, на которых выполняется логическая схема основного узла, принципиальная электрическая схема устройства и перечень элементов, а также пояснительной записки объемом 30-40 страниц формата А4. Текстовая и графическая части курсового проекта выполняются с помощью компьютерных средств. Требования к оформлению курсовых проектов подробно изложены в [5], а кратко – в приложении В.
Примечания
1 Исходные данные для проектирования по темам № 1-3, выдаваемые преподавателем, могут отличаться от значений, указанных в таблицах 2, 3 и 5.
Курсовой проект, который выполнен по заданию без подписи преподавателя, на проверку не принимается.
3 На проверку студенты сдают чертеж, распечатку пояснительной записки и электронный вариант курсового проекта (текстовую часть – в формате RTF, а графическую часть – в формате AutoCAD 2006). Электронный вариант представляет собой папку, в которой титульный лист, задание, разделы курсового проекта и чертежи являются отдельными документами. На диске следует маркером указать фамилию студента, шифр группы и номер варианта.
4 В распечатку пояснительной записки следует подшивать рукописный вариант задания, подписанный преподавателем, и распечатку электронного варианта. Примеры оформления заданий приведены в приложении Б.
Таблица 1 – Номера вариантов заданий к курсовому проекту
| Номер по списку для ДФО или номер зачетки для ЗФО | Номер варианта задания к курсовому проекту |
| 1.1 | |
| 2.1 | |
| 3.1 | |
| 1.2 | |
| 2.2 | |
| 3.2 | |
| 1.3 | |
| 2.3 | |
| 3.3 | |
| 1.4 | |
| 2.4 | |
| 3.4 | |
| 1.5 | |
| 2.5 | |
| 3.5 | |
| 1.6 | |
| 2.6 | |
| 3.6 | |
| 1.7 | |
| 2.7 | |
| 3.7 | |
| 1.8 | |
| 2.8 | |
| 3.8 | |
| 1.9 | |
| 2.9 | |
| 3.9 | |
| 1.10 | |
| 2.10 | |
| 3.10 | |
| Примечание – Первая цифра слева в номере варианта задания означает номер темы, а вторая – номер варианта внутри темы. |
ТЕМА № 1. УСТРОЙСТВО УМНОЖЕНИЯ ДВОИЧНЫХ ЧИСЕЛ
1.1 Описание принципа работы заданной структурной электрической схемы устройства умножения двоичных чисел
Структурная электрическая схема устройства умножения четырехразрядных двоичных чисел представлена на рисунке 1.
Рисунок 1 – Устройство умножения двоичных чисел.
Схема электрическая структурная
Рассмотрим назначение узлов, входящих в структурную схему устройства.
Умножитель Y3 предназначен для умножения четырехразрядных двоичных чисел A и B, представленных разрядами 
, 
, 
, 
и 
, 
, 
, 
. На выходе умножителя формируется восьмиразрядное произведение Q, представленное разрядами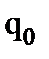 
, 
,…, 
.
Регистр Y1 предназначен для параллельного ввода четырехразрядного множимого A в двоичной системе счисления (СС). Значение множимого A может меняться в пределах от 0 до 15 в десятичной СС.
Счетчик Y2 предназначен для параллельного ввода четырехразрядного множителя B в двоичной СС. Значение множителя B также может меняться от 0 до15 в десятичной СС.
Регистр Y4 предназначен для параллельного вывода результата умножения, который представляет собой восьмиразрядное кодовое слово.
Загрузка сомножителей и запись результата умножения синхронизируется тактовыми импульсами 
. Причем ввод сомножителей осуществляется по отрицательным фронтам тактовых импульсов, а вывод результата умножения – по положительным.
Процесс функционирования устройства поясняется временной диаграммой, которая представлена на рисунке 2.
Рисунок 2 – Временная диаграмма, поясняющая процесс функционирования устройства
В момент времени 
по отрицательному фронту тактового импульса начинается ввод сомножителей в регистр Y1 и счетчик Y2 (рисунок 1). К моменту времени 
ввод заканчивается, и начинается процесс умножения в умножителе Y3. Этот процесс в худшем случае завершается к моменту времени 
. Затем по положительному фронту тактового импульса результат умножения записывается в регистр Y4 и т.д. При подаче низкого уровня напряжения на вход 
(рисунок 1) устройство сбрасывается в исходное нулевое состояние.
Рассмотрим процесс умножения двоичных чисел на примере умножения заданных чисел[1]), например: 
и 
. Умножение выполним, начиная с младшего разряда множителя:
| 1 1 0 1 |
  
|
| – множимое |
| × |
| 1 0 1 1 |
   
|
| 1 1 0 1 |
| 1 1 0 1 |
| 0 0 0 0 |
| + |
| 1 1 0 1 |
| + |
| + |
| 1 0 0 0 1 1 1 1 |
       
|
| – множитель |
| – частичные произведения |
| – полное произведение |
|
Таким образом, при умножении двоичных чисел формируются частичные произведения, сдвигаются и суммируются. Сравним результаты умножения чисел A и B в двоичной и десятичной СС. Для этого преобразуем результат умножения в десятичную систему счисления:
Они совпадают и равны 
.
1.2 Задание на проектирование к теме № 1
Описать принцип построения и разработать логическую схему матричного умножителя четырехразрядных двоичных чисел. Разработать логическую схему суммирующего четырехразрядного недвоичного счетчика на JK-триггерах с коэффициентом пересчета заданным в таблице 2. В принципиальной электрической схеме устройства использовать двоичный счетчик. Разработать в основном базисе логическую схему двухразрядного двоичного сумматора с последовательным переносом. Разработать принципиальную электрическую схему устройства умножения по заданной структурной схеме (рисунок 1) на микросхемах схемотехники КМОП, серии которых указаны в таблице 2.
Таблица 2 – Исходные данные для проектирования устройства умножения двоичных чисел
| Номер варианта | Значение числа A (P=10) | Значение числа B (P=10) | Серии микросхем | |
| 1.1 | 1594, 5564 | |||
| 1.2 | 1554, 1564 | |||
| 1.3 | 1594, 5564 | |||
| 1.4 | 1554, 1564 | |||
| 1.5 | 1594, 5564 | |||
| 1.6 | 1554, 1564 | |||
| 1.7 | 1594, 5564 | |||
| 1.8 | 1554, 1564 | |||
| 1.9 | 1594, 5564 | |||
| 1.10 | 1554, 1564 |
Описать работу принципиальной электрической схемы устройства в течение одного периода сигнала синхронизации при умножении заданных в таблице 2 чисел A и B. Пример оформления задания к теме № 1 приведен в приложении Б.
1.3 Назначение и принцип построения матричных умножителей двоичных чисел
Умножителем называется комбинационное цифровое устройство, формирующее на выходе число Q, равное произведению входных двоичных чисел A и B [9, 10].
Условное графическое обозначение умножителя представлено на рисунке 3.
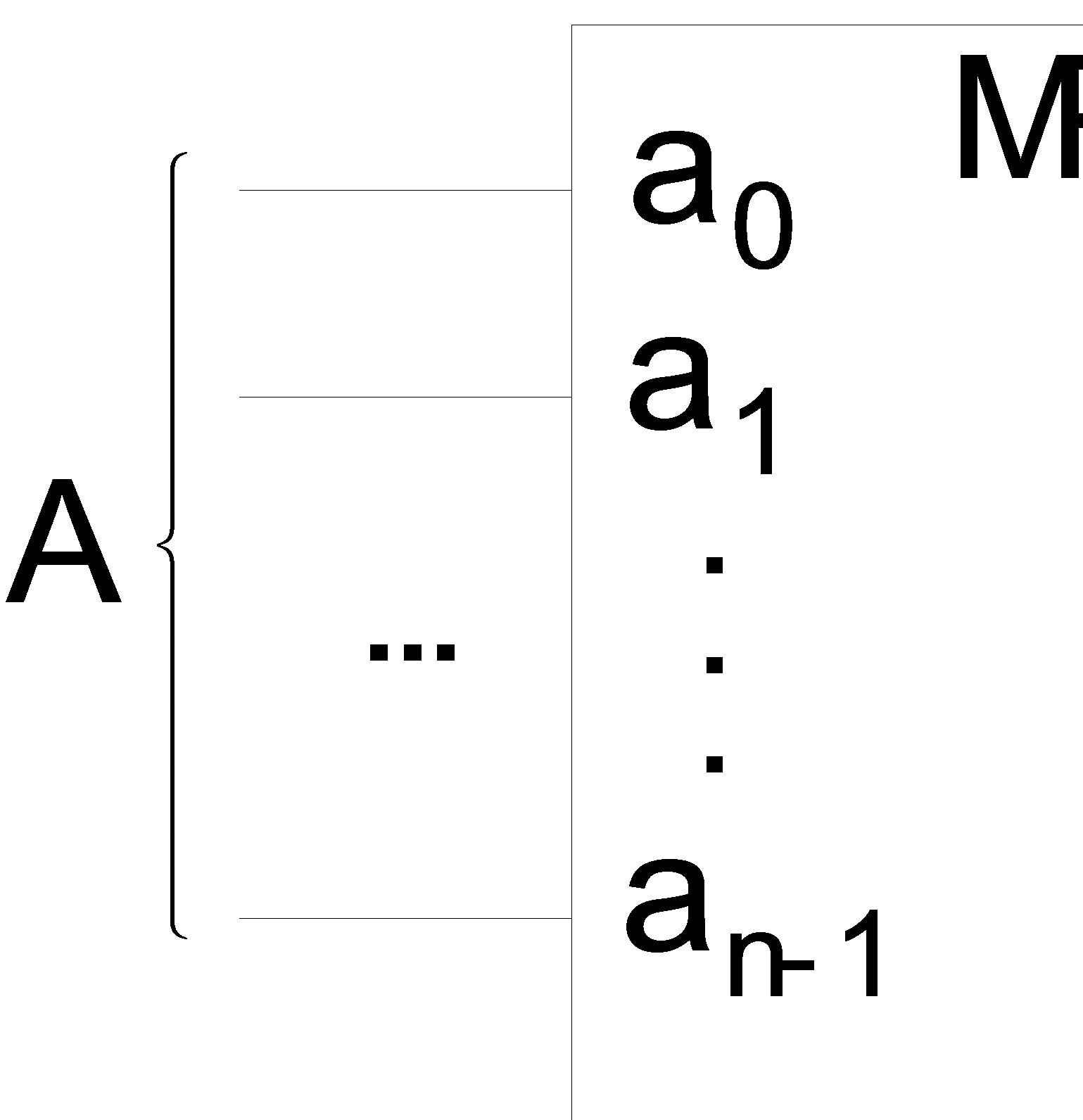
Рисунок 3 – Условное графическое обозначение умножителя
Предполагается, что числа A, B и Q представлены в двоичной позиционной системе счисления. При этом, если число A имеет n двоичных разрядов (, ,…, 
), число B имеет m двоичных разрядов (, ,…, 
), то для представления максимального значения произведения 
требуется n+m двоичных разрядов числа Q (, ,…, 
). Каждый разряд произведения является логической (переключательной) функцией аргументов , ,…, и , ,…, , значения которого можно найти из таблиц умножения либо путем выполнения умножения для заданных значений аргументов. Однако прямой логический синтез схемы умножителя, основанный на представлении функции выражениями в булевой алгебре, ввиду громоздкости неэффективен. Исключения составляют простейшие случаи перемножения одноразрядных или двухразрядных двоичных чисел. Поэтому на практике используют методы синтеза, основанные на разложении операции умножения на последовательность простейших арифметических действий с одноразрядными числами. Полагая, что в двоичном представлении значения чисел A и B определяются выражениями:
и 
(1)
произведение 
можно записать в форме двойной суммы:
(2)
Группируя члены с одинаковыми весовыми коэффициентами 
, преобразуем (2) к виду:
(3)
Из полученной формулы (3) видно, что для вычисления значения k-го разряда произведения необходимо выполнить совокупность произведений одноразрядных чисел (
, 
), для которых сумма индексов i + j = k. Затем надо последовательно складывать эти произведения. При добавлении к сумме новых слагаемых возможно появление переноса в следующий k + 1-й разряд. Поэтому при нахождении k-го разряда произведения нужно к сумме членов (, ) добавить все переносы, получаемые при сложении аналогичных членов для предыдущего k – 1 разряда.
Порядок, в котором производится сложение произведений ( ) и переносов из предыдущего разряда, значения не имеет.
Указанные действия мы выполняем, производя перемножение двоичных чисел на бумаге. Так, вычисляя произведение десятичных
| 1 1 0 1 |
| × |
| 1 0 1 1 |
| 1 1 0 1 |
| 1 1 0 1 |
| 0 0 0 0 |
| + |
| 1 1 0 1 |
| + |
| + |
| 1 0 0 0 1 1 1 1 |
|
|
чисел
[2]) делаем следующую запись:
Штриховой линией обведены произведения (
), для которых сумма индексов i + j = 4. В результате сложения этих произведений получаем значение 1. Однако после прибавления переноса из предыдущего третьего разряда четвертый разряд результата принимает значение 0 и формируется перенос в следующий пятый разряд .
Арифметическое перемножение одноразрядных чисел () реализуется конъюнктором, поскольку логическое умножение совпадает с арифметическим.
В качестве элементарной ячейки умножителя используют устройство, показанное на рисунке 4 а.
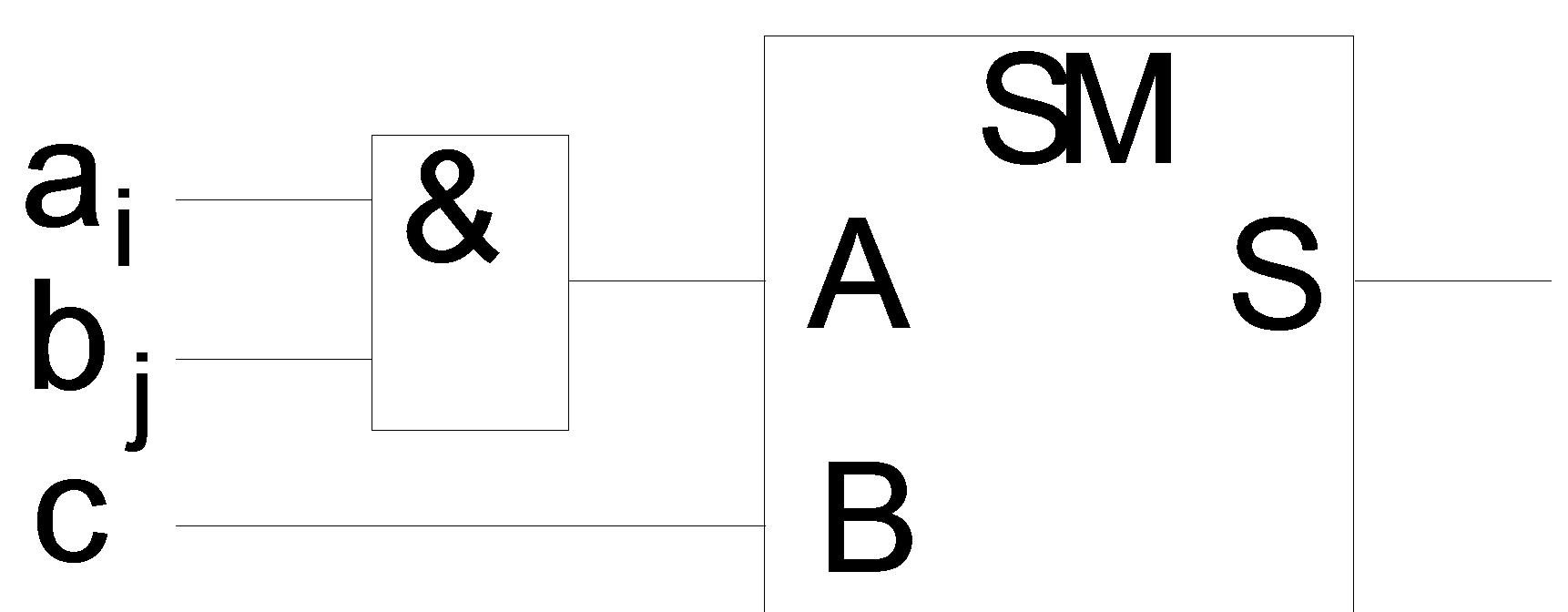
Рисунок 4 – Элементарная ячейка умножителя. Логическая схема (а) и символическое обозначение (б)
Операция, реализуемая такой ячейкой, задается выражением ab + c + d, где a, b, c и d – одноразрядные двоичные числа. Результат, получаемый на выходе ячейки, представляется одноразрядной частичной суммой S и переносом C.
Из выражения (2) видно, что для нахождения произведения 
требуется получить mn одноразрядных произведений (aibj), по одному для каждой возможной комбинации индексов i, j. Именно столько элементарных ячеек требуется для построения умножителя. Для наглядности представления структуры умножителя элементарные ячейки на структурной схеме целесообразно изображать в символической форме, как показано на рисунке 4 б. Поскольку такое обозначение содержит в явной форме сомножители ai, bj, участвующие в операции, реализуемой ячейкой, то связи, предназначенные для подведения к ячейкам этих сомножителей, можно на структурной схеме умножителя не обозначать.
Один из вариантов структурной схемы умножителя для m = n = 4 показан на рисунке 5.
Рисунок 5 – Умножитель четырехразрядных двоичных чисел.
Схема электрическая структурная
Каждый горизонтальный ряд элементарных ячеек выполняет умножение числа A на один из разрядов множителя B и суммирует полученное произведение с результатом аналогичной операции, реализуемой предыдущим (верхним) рядом. При этом частичная сумма с выходов элементарных ячеек верхнего ряда поступает на входы d элементарных ячеек следующего за ним ряда. Входы c использованы для приема переноса, возникающего при сложении произведений (aibj).
В результате сдвига вправо элементов каждого следующего горизонтального ряда по отношению к предыдущему на одну позицию в каждом столбце элементов сумма индексов сомножителей ai, bj совпадает с номером к столбца и индексом разряда qk произведения, формируемого в этом столбце.
На суммирующие входы d самого верхнего горизонтального ряда элементов и на входы переноса c крайних левых элементов в каждом ряду подают нули. При этом на выходах элементов верхнего ряда формируется (n + 1) – разрядная частичная сумма S0 = Ab0. Младший разряд частичной суммы S0 является младшим разрядом q0 произведения AB, поскольку других произведений, кроме a0b0, сумма индексов которых равна 0, нет. Более старшие разряды частичной суммы S0 складываются во втором ряду элементарных ячеек с произведением Ab1, формируя на выходах следующую частичную сумму S1, младший разряд которой является вторым по старшинству разрядом произведения q1. Аналогично формируются частичные суммы S2, S3, причем значение частичной суммы S3 определяет старшие разряды произведения (q3,…,q7).
Умножитель, построенный по схеме на рисунке 5, можно использовать как секцию умножителя с более высокой разрядностью.
Для определения быстродействия умножителя следует вычислить суммарное время выполнения операции умножения, которое определяется длиной критического пути прохождения сигнала со входа на выход. Для простоты длина критического пути оценивается максимальным числом элементарных ячеек, которые сигнал должен пройти от входного нулевого разряда сомножителя до старшего разряда результата. Для схемы, показанной на рисунке 5, длина критического пути в общем случае составляет n + 2 (m - 1) и, следовательно, равна 10.
Таким образом, для определения суммарной задержки распространения сигнала в умножителе необходимо определить задержку распространения сигнала в элементарной ячейке и умножить на длину критического пути. Задержка распространения сигнала в элементарной ячейке умножителя определяется суммой среднего времени задержки распространения сигнала в конъюнкторе и одноразрядном сумматоре.
Исходя из вышесказанного, суммарное среднее время задержки распространения сигнала в умножителе можно определить по формуле.
(4)
где – среднее время задержки распространения сигнала одного конъюнктора, нс;
– среднее время задержки распространения сигнала одноразрядного сумматора, нс.
1.4 Методические указания по разработке разделов проекта к теме № 1
Синтез заданного счетчика выполните по методике, приведенной в приложении А.
Логическую схему двухразрядного двоичного сумматора с последовательным переносом разработайте в основном базисе. Для этого на основании логических функций (5) и (6) запишите логические функции для выходов суммы S0,S1 и переноса C1,C2. Логическую схему вычертите в формате А4 и выполните указания раздела 5.
Как отмечалось выше, прямой логический синтез умножителя на практике не используется. Поэтому на основании структурной схемы умножителя (рисунок 5) и логической схемы секции умножителя при n = 4, m = 2 (рисунок 6) разработайте логическую схему умножителя четырехразрядных двоичных чисел при n = 4, m = 4.
Рисунок 6 – Логическая схема секции умножителя при n = 4, m = 2
В логической схеме используйте четырехразрядные двоичные сумматоры. Для передачи переноса от одной элементарной ячейки к другой в каждом ряду структурной схемы умножителя (рисунок 5) в сумматорах имеются внутренние связи. На рисунке 6 указаны обозначения входных и выходных сигналов в соответствии со структурной схемой умножителя (рисунок 5).
Логическую схему умножителя (лист 1) вычертите в формате А3 и выполните указания раздела 5. На логической схеме обозначьте входные и выходные сигналы в соответствии с рисунками 5 и 6. Все надписи и обозначения сигналов выполните чертежным шрифтом 3,5.
Принципиальную электрическую схему устройства умножения (лист 2) разработайте на выбранных микросхемах на основе заданной структурной схемы (рисунок 1) и разработанной логической схемы умножителя (лист 1). Принципиальную схему вычертите в формате А2 и выполните указания раздела 5 данных методических указаний.
ТЕМА № 2. УСТРОЙСТВО СУММИРОВАНИЯ ДВОИЧНЫХ ЧИСЕЛ
2.1 Описание принципа работы заданной структурной электрической схемы устройства суммирования двоичных чисел
Структурная электрическая схема устройства суммирования двоичных чисел представлена на рисунке 7.
Рисунок 7 – Устройство суммирования двоичных чисел.
Схема электрическая структурная
Рассмотрим назначение узлов, входящих в структурную схему устройства.
Четырехразрядный двоичный сумматор с параллельным переносом Y3 предназначен для суммирования четырехразрядных двоичных чисел A и B, представленных разрядами a3…a0 и b3…b0. На выходе сумматора формируется четырехразрядная сумма S, представленная разрядами s3…s0, а также перенос C в пятый разряд.
Работа устройства синхронизируется тактовыми импульсами UС, причем ввод слагаемых осуществляется по отрицательному перепаду сигнала синхронизации, суммирование – при низком уровне сигнала синхронизации, а вывод результата – по положительному перепаду.
Процесс функционирования устройства поясняется временной диаграммой, которая представлена на рисунке 8.
Рисунок 8 – Временная диаграмма, поясняющая процесс функционирования устройства
В момент времени t1 по отрицательному перепаду тактового импульса UС начинается ввод слагаемых. К моменту времени t2 ввод заканчивается и начинается суммирование. К моменту времени t3 суммирование заканчивается, и по положительному перепаду сигнала синхронизации UС результат суммирования записывается в регистр Y4 и триггер переноса Y5.
При подаче низкого уровня напряжения на вход 
(рисунок 7) устройство сбрасывается в исходное нулевое состояние.
Рассмотрим пример суммирования двоичных чисел, заданных в шестнадцатеричной системе счисления[3]).
Например, А = F(16) и B = 2(16). Переведем заданные числа в двоичную систему счисления и выполним суммирование:
| a3 | a2 | a1 | a0 | ||||||||
| A | = | ||||||||||
| + | |||||||||||
| B | = | ||||||||||
| b3 | b2 | b1 | b0 | ||||||||
| A+B | = | ||||||||||
| C | s3 | s2 | s1 | s0 |
Таким образом, полный результат суммирования А + В = 11(16), так как имеется перенос C в пятый разряд.
2.2 Задание на проектирование к теме № 2
Описать принцип построения и разработать в базисе И-НЕ логическую схему четырехразрядного двоичного сумматора с параллельным переносом. Разработать логическую схему суммирующего четырехразрядного недвоичного счетчика на JK-триггерах с коэффициентом пересчета Kпер, заданным в таблице 3. В принципиальной электрической схеме устройства суммирования использовать двоичный счетчик. Разработать принципиальную электрическую схему устройства суммирования по заданной структурной схеме (рисунок 7) на микросхемах схемотехники КМОП, серии которых указаны в таблице 3.
Таблица 3 – Исходные данные для проектирования устройства суммирования двоичных чисел
| Номер варианта | Значение числа A (P=16) | Значение числа B (P=16) | Серии микросхем | К пер |
| 2.1 | E | 1594, 5564 | ||
| 2.2 | C | 1554, 1564 | ||
| 2.3 | D | E | 1594, 5564 | |
| 2.4 | E | 1554, 1564 | ||
| 2.5 | B | 1594, 5564 | ||
| 2.6 | A | C | 1554, 1564 | |
| 2.7 | D | 1594, 5564 | ||
| 2.8 | E | 1554, 1564 | ||
| 2.9 | B | E | 1594, 5564 | |
| 2.10 | F | B | 1554, 1564 |
Описать работу принципиальной электрической схемы устройства суммирования в течение одного периода сигнала синхронизации UC при суммировании заданных в таблице 3 чисел A и B.
2.3 Назначение и принцип построения четырехразрядных двоичных сумматоров с параллельным переносом
Основной операцией при выполнении арифметических действий в современных цифровых системах является сложение. Поэтому основным блоком операционных устройств обычно является сумматор, который используется также для вычитания, умножения, деления, преобразования чисел в дополнительный код, код «с избытком 3» и в ряде других операций [7, 8, 9].
Суммирование многоразрядных двоичных чисел производится путем их поразрядного сложения с переносом между разрядами. Поэтому основным узлом многоразрядных сумматоров является комбинационный одноразрядный сумматор, который выполняет арифметическое сложение одноразрядных двоичных чисел ai, bi и переноса из соседнего младшего разряда ci, образуя на выходах значение суммы Si и переноса в старший разряд Ci+1.
Условное графическое обозначение одноразрядного двоичного сумматора приведено на рисунке 9.
Рисунок 9 – Условное графическое обозначение одноразрядного сумматора
В таблице 4 приведена таблица истинности одноразрядного сумматора.
Таблица 4 – Таблица истинности одноразрядного сумматора
| ai | bi | ci | Si | Ci+1 |
Логические функции для выходов Si и Ci+1 одноразрядного сумматора, записанные в СДНФ по данным таблицы 4, после минимизации имеют вид:
Как следует из выражения (5), функцию Si удобно реализовать с помощью двух логических элементов «Исключающее ИЛИ», которые часто называют полусумматорами. Функциональная схема одноразрядного сумматора на основе двух полусумматоров показана на рисунке 10.
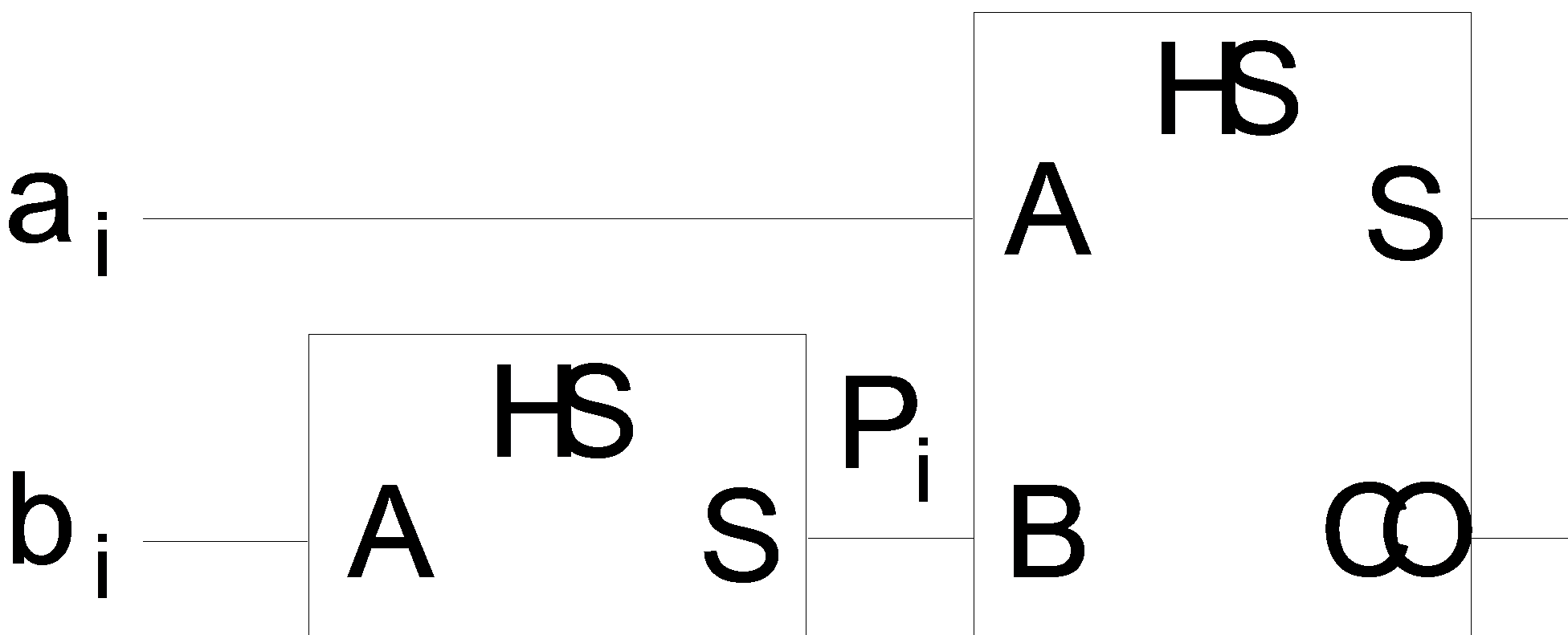
Рисунок 10 – Функциональная схема одноразрядного сумматора на основе двух полусумматоров
Для суммирования двух многоразрядных двоичных чисел на каждый разряд необходим один одноразрядный сумматор. Только в младшем разряде можно использовать полусумматор. На рисунке 11 приведена функциональная схема четырехразрядного параллельного сумматора с последовательным переносом.
В ее младшем разряде также используется полный одноразрядный сумматор. При этом наличие входа переноса C0 позволяет рассматривать схему как четырехразрядную секцию сумматора с большой разрядностью. Такая секция может быть реализована в виде микросхемы.
Существенным недостатком сумматоров с последовательным переносом является большая задержка (
) выходного сигнала Cn в цепи переноса, связанная с его последовательным прохождением через все одноразрядные сумматоры, каждый из которых имеет задержку переноса tc. В результате tCn = ntc, а задержка образования n-го разряда суммы tSn = tS + (n – 1) tC, где tS – задержка суммы одноразрядного сумматора. При числе разрядов n > 4…8 времена tSn, tCn оказываются весьма значительными, поэтому для повышения быстродействия в сумматорах обычно применяют ускоренные способы формирования переноса.
Наиболее часто используется одновременное (параллельное) формирование переноса для нескольких разрядов. При этом вводятся вспомогательные функции генерации переноса 
и распространения переноса 
.Тогда выражение (6) можно представить в следующем виде:
(7)
Из выражения (7) следует, что сигнал переноса на выходе i‑го разряда генерируется самим разрядом (Gi = 1) при ai = bi = 1 независимо от результата переноса из соседнего младшего разряда. Следовательно, можно передавать сигнал переноса для обработки старших разрядов, не дожидаясь окончания формирования переносов из младших разрядов. Однако если только один из сигналов ai, bi равен единице, то перенос в следующий разряд будет иметь место только при наличии переноса из предыдущего разряда (Pi = 1, ci = 1). В этом случае 
Именно этот случай будет реализован, если значения функций Gi, Pi снимать с выходов первого полусумматора схемы, показанной на рисунке 10.
Рисунок 11 – Функциональная схема четырехразрядного параллельного сумматора с последовательным переносом
Таким образом, сигналы переноса в каждом разряде формируются одновременно в соответствии с выражением (7):
В обобщенном виде получаем:
(8)
Для образования переносов C1, C2,…, Ci+1 необходимо предварительно получить функции Pi, Gi для каждого разряда. Как видно из выражения (8), сложность функций и, соответственно, схем формирования переноса Ci+1 быстро возрастает при увеличении числа разрядов i. Поэтому данный способ используется при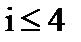 
.
Устройство, реализующее функции (8), называют схемой ускоренного переноса (СУП). На функциональных схемах его обозначают символом GRP.
Функциональная схема четырехразрядной секции сумматора с ускоренным (параллельным) переносом показана на рисунке 12.
На рисунке 12 изменено условное графическое обозначение одноразрядных сумматоров, так как от них выход переноса Ci+1 не требуется, достаточно одного выхода суммы S. Для реализации ускоренного переноса в одноразрядные сумматоры необходимо ввести дополнительные логические элементы для формирования сигналов Gi, Pi в соответствии с выражением (7).
Рисунок 12 – Функциональная схема четырехразрядной секции сумматора с ускоренным (параллельным) переносом
2.4 Методические указания по разработке разделов проекта к теме № 2
Логическую схему четырехразрядного двоичного сумматора с параллельным переносом (лист 1) постройте в базисе И-НЕ.
Для этого на основании логических функций (5), (7) и (8) запишите логические функции для выходов суммы S0…S3 и переноса C1…C4 и преобразуйте их в базис И-НЕ. При этом для каждого сигнала переноса отдельно запишите выражения для сигналов генерации переноса G0…G3 и