МиНИСТЕРСТВО НАУКИ и высшего образования РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ государственное БЮДЖЕТНОЕ образовательное
Учреждение высшего образования
«тюменский ИНДУСТРИАЛЬНЫЙ университет»
КОНТРОЛЬНАЯ РАБОТА
по дисциплине: «Автоматизация технологических процессов добычи нефти и газа»
на тему: «РАСЧЕТ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ»
Вариант № 3
Выполнил:
студент гр. ЭДГбз 16-1
Ф.И.О. Машаров А.М.
Проверил:
Андриянов А.М., к.т.н., доцент
Тюмень
ТИУ
Внутри блоков структурной схемы записываем передаточные функции звеньев (рис.1).

Рис. 1 Структурная схема САР расхода
Дано:
То=9c; Кпр=0.4; Киу=1; Тиу=4с; Кп=1; Ти=0,5с
Объект управления представляет собой участок трубопровода от измерительного преобразователя до исполнительного устройства.
Передаточные функции объекта управления, исполнительного устройства, измерительного преобразователя и регулятора имеют вид:

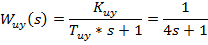

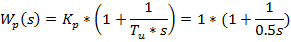
Находим передаточную функцию разомкнутой системы, состоящую из последовательно соединенных звеньев: регулятора расхода, исполнительного устройства и объекта управления.

Находим передаточную функцию замкнутой системы:

Знаменатель передаточной функции замкнутой системы называется характеристическим уравнением (полиномом). Выписываем его, приравниваем к нулю и анализируем.

Исследуем устойчивость САР по критерию Гурвица.
Характеристическое уравнение (полином) замкнутой системы имеет вид:

Составляем главный определитель Гурвица
| 6.5 | 0.4 | ||
| ∆3= | 0.7 | ||
| 0.4 |
Определяем диагональные миноры этого определителя
| ∆1= | 6.5 | > | ||||
| ∆2= | 6,5 | 0,4 | ||||
| 0,7 | = | -2,65 | < |
| 6.5 | 0.4 | ||
| ∆3= | 0.7 | ||
| 0.4 |
=6.5*0.7*0.4+18*6.5*0+0*0*0.4-0*0.7*0-6.5*6*0-18*0.4*0.4=1.82-2.88= -1.06<0
Или 0,4*∆2=0,4*-(2,65)= -1,06˂0
Определители всех трёх порядков отрицательные, следовательно система неустойчива.
Определение устойчивости САР по критерию Михайлова.
Построить кривую-Михайлова и определить устойчивость системы автоматического регулирования, если характеристическое уравнение имеет вид:

Решение.
Заменяем s на jω, в результате чего получим:



Выделим в характеристическом уравнении на вещественную и мнимую части:
(𝜔) = 𝑅{𝑀(𝑗𝜔)} = 0.4 – 6.5 
(𝜔) = 𝐽{𝑀(𝑗𝜔)} = 0.7𝜔 − 18 
При ω= 0 получим первую точку годографа Михайлова. Заносим значение в таблицу и отмечаем координаты точки при ω = 0 на комплексной плоскости:
(𝜔) = 𝑅{𝑀(𝑗𝜔)} = 0.4
𝑌 𝜔 = {(𝑗𝜔)} = 0
Определяем вторую точку пересечения годографа с осями координат. Значение частоты ω, при которой характеристика пересекает мнимую ось, определяем, приравнивая вещественную часть к нулю:
(𝜔) = 𝑅𝑒{𝑀(𝑗𝜔)} = 0
0.4 – 6.5  = 0
= 0
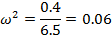
𝜔 =  = 0.24
= 0.24
Находим значение мнимой части при этой частоте:

Заносим значение в табл. 1 и отмечаем координаты точки при ω = 0.24 на комплексной плоскости (рис. 1).
Находим третью точку пересечения кривой Михайлова с осями координат. Значение ω, при котором годограф пересекает вещественную ось между третьим и вторым квадрантами, находим, приравнивая мнимую часть к нулю:

0.7𝜔 − 18  =0
=0
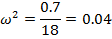
𝜔 =  = 0.2
= 0.2
Находим значение вещественной части при этой частоте:

Находим значения мнимой и вещественной частей при значении ω =  :
:


На рис. 2 показана расчетная кривая Михайлова.
Таблица 1
| ω | 0,05 | 0,1 | 0,105 | 0,2 | 0,3 | 0,4 | 0,5 | |
| X(ω) | 0,4 | 0,38375 | 0,335 | 0,3283375 | 0,14 | -0,185 | -0,64 | -1,225 |
| Y(ω) | 0,03275 | 0,052 | 0,05266275 | -0,004 | -0,276 | -0,872 | -1,9 |
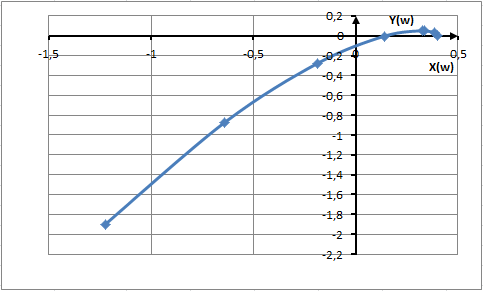
Рис. 2 Кривая Михайлова
Годограф Михайлова начинается на положительной полуоси и раскручиваясь против часовой стрелки заходит на 4 квадрант, что соответствует годографу неустойчивой системы. Следовательно система неустойчива.