Физический смысл основного уравнения МКТ заключается в том, что давление идеального газа - это совокупность всех ударов молекул о стенки сосуда. Это уравнение можно выразить через концентрацию частиц, их среднюю скорость и массу одной частицы:
p – давление молекул газа на границы емкости,
m0 – масса одной молекулы,
n - концентрация молекул, число частиц N в единице объема V;
v2 - средне квадратичная скорость молекул.
Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа
Таблица значений средней квадратичной скорости молекул некоторых газов
Для того чтоб понять, откуда же у нас получается эта формула, мы выведем среднюю квадратичную скорость молекул. Вывод формулы начинается с основного уравнения молекулярно кинетический теории (МКТ):
Где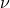 
у нас количество вещества, для более легкого доказательства, возьмем на рассмотрение 1 моль вещества, тогда у нас получается:
Если посмотреть, то PV это две третьих средней кинетической энергии всех молекул (а у нас взят 1 моль молекул):
Тогда, если приравнять правые части, у нас получается, что для 1 моля газа средняя кинетическая энергия будет равняться:
Но средняя кинетическая энергия, так же находится, как:
А вот теперь, если мы приравняем правые части и выразим из них скорость и возьмем квадрат,Число Авогадро на массу молекулы, получается Молярная масса 
то у нас и получится формула для средней квадратичной скорости молекулы газа:
А если расписать универсальную газовую постоянную, как 
, и за одно молярную массу 
, то у нас получится?
В Формуле мы использовали:
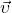— Средняя квадратичная скорость молекул
— Постоянная Больцмана
— Температура
— Масса одной молекулы
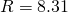— Универсальная газовая постоянная
— Молярная масса
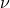— Количество вещества
— Средняя кинетическая энергия молекул
— Число Авогадро
кинетическая интерпретация абсолютной температуры
Эта величина, очевидно, должна зависеть от температуры, поскольку в нее входит степень покрытия поверхности 0, зависящая от температуры. Отсюда возникает противоречие если кинетическое уравнение правильно, то из него вытекает непостоянство величины Е в достаточно широком температурном интервале. Однако авторы получили согласие величины Е с расчетными. Следовательно, или уравнение кинетики неверно, или интервал температур слишком узок. Согласие экспериментальной величины Е с рассчитанной с помощью теории абсолютных скоростей реакции по тем же причинам также иллюзорно.. Это видно и из того, что в работе неточно принимается равенство нулю энтропии активации. Если неточный расчет подтверждает данные с неточной интерпретацией, то полученное согласие только ухудшает дело. Таким образом, недостаточно обоснованная трактовка кинетических данных существенно снижает ценность этой интересной работы
18. Средняя кинетическая энергия молекулы. Разделение энергии по степеням свободы. Закон Максвелла о разделении молекул газа в зависимости от скоростей. Исследование Штерна.
Выражение для энергии поступательного движения молекулы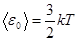 
выведено для одноатомного газа, где молекула рассматривалась как материальная точка. Положение материальной точки в пространстве определяется тремя величинами, т.е. тремя координатами. Однако, для многоатомной молекулы наряду с поступательным движением возможны также ее вращение и колебания атомов входящих в состав молекулы. Поэтому положение в пространстве многоатомной молекулы определяет большее количество величин.
Количество независимых величин, с помощью которых определяется положение системы в пространстве называется числом степеней свободы.
Если средняя кинетическая энергия поступательного движения равна 
, то нетрудно заметить, что на одну степень свободы приходится 
энергии. Обобщая сказанное, средняя кинетическая энергия любой молекулы будет 
,
где i – суммарное количество поступательных, вращательных и колебательных степеней свободы.
Количество колебательных степеней свободы для газа равно нулю. Максимальное количество степеней свободы, которым может обладать молекула равна 6 – 3 степени свободы поступательного движения и 3 степени свободы вращательного.
Для одноатомной молекулы i = 3.
Двухатомную молекулу можно уподобить двум материальным точкам, жестко связанным между собой, как, например, гантели. Такая молекула может поступательно двигаться вдоль осей X, Y, Z. Расположив ее вдоль одной из осей, она может вращаться вокруг двух других, т.е. i = 3пост + 2вращ. = 5.
Начиная с трехатомной, у всех молекул i = 6.
Средняя энергия (из вывода основного уравнения кинетической теории газов), приходящаяся на одну молекулу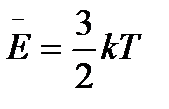 
. Если считать молекулу шариком (как в одноатомном газе), то средняя энергия такой частицы определяется средней кинетической энергией ее поступательного движения. Энергию эту можно представить как сумму трех слагаемых – кинетических энергий движения молекулы по трем взаимно перпендикулярным направлениям: 
,
где vx, vy, vz – составляющие скорости молекул по трем осям координат. Из-за хаотичности молекулярного движения можно считать, что средние значения кинетических энергий по трем направлениям равны друг другу:
. (1)
Так как согласно основному уравнению кинетической теории 
,
то каждое из трех слагаемых равенства (1) равно kT /2.
Разделение кинетической энергии частицы на три независимые составляющие связано с тем, что частица рассматривается как свободная материальная точка, обладающая тремя степенями свободы.
Число степеней свободы - наименьшее число линейно независимых координат, которые полностью определяют положение тела в пространстве. Значит, на каждую степень свободы одноатомной молекулы приходится энергия, равная kT /2. Естественно было предположить, что если бы молекула газа обладала еще какими-нибудь степенями свободы, то и на каждую их них пришлась бы кинетическая энергия kT /2. Действительно, в классической статистической физике такая теорема доказывается (Больцман): в совокупности большого числа молекул, находящемся в тепловом равновесии при температуре Т средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна kT /2.
Эта теорема называется законом равномерного распределения кинетической энергии по степеням свободы, или, законом равнораспределения.
Двух- и многоатомные газы отличаются от одноатомных числом степеней свободы. При низких температурах молекулы участвуют только в поступательном движении. По мере повышения Т молекулы начинают совершать и вращательные движения. И лишь при высоких температурах она совершает все три вида движения (добавляется колебательное). Степень свободы колебательного движения: iкол = 3N-5 (если атомы располагаются на одной прямой) или iкол = 3N-6, где N – число атомов в молекуле.
Полное число степеней свободы:
| Молекула | iпост | iвр | iкол | i |
| Одноатомная | - | - | ||
| Двухатомная с жесткой связью | - | |||
| Двухатомная с гибкой связью | ||||
| Трехатомная с жесткой связью | - | |||
| Трехатомная с гибкой связью |
Закон Максвелла о распределении молекул по скоростям
Если газ находится в равновесии, молекулы движутся хаотически, и все направления их движения равновероятны. Скорости молекул могут быть самыми различными по модулю и при каждом соударении с другими молекулами изменяются случайным образом.
В газе, находящемся в состоянии равновесия, устанавливается стационарное распределение молекул по скоростям, подчиняющееся определенному статистическому закону. Этот закон был выведен теоретически Дж. Максвеллом. Максвелл предполагал, что вещество состоит из очень большого числа тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Также предполагалось, что силовые поля на газ не действуют.
Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по модулям скоростей. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), скорости которых заключены в этом интервале.
Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, то есть:
dN(v)/N=f(v)dv, откуда f(v)=dN(v)/Ndv (28)
Применяя методы теории вероятностей, Дж. Максвелл нашел вид функции распределения молекул идеального газа по модулям скоростей хаотического движения:
(29)
Из (29) следует, что конкретное распределение зависит от рода газа (от массы молекулы) и от его термодинамической температуры. Очевидно, что функция распределения не зависит ни от давления, ни от объема газа. График функции распределения имеет вид, показанный на рис. 5.
Рис. 5. График функции распределения молекул по скоростям
Выражение dN(v)/N=f(v)dv представляет собой вероятность встретить молекулу со скоростью, принадлежащей интервалу (v;v+dv). Эта вероятность равна площади заштрихованной полоски с основанием dv (рис. 5). Относительная доля молекул, имеющих определенную скорость, равна нулю.
Площадь под кривой f(v) равна вероятности достоверного события – встретить молекулу со скоростью, принадлежащей интервалу (0;∞), то есть равна единице. Это означает, что функция удовлетворяет условию нормировки:
f(v)dv=1 (30)
Наиболее вероятная vв, средняя арифметическая <v> и среднеквадратичная скорости <vкв> молекул.
Наиболее вероятная скорость соответствует максимуму функции распределения, ведь именно этой скоростью будет обладать наибольшее число молекул. Ее значение найдется из условия экстремума функции f(v):
vв=√(2kT/m0)=√(2kNAT/m0NA)=√(2RT/M) (31)
Отсюда видно, что при увеличении температуры T максимум кривой распределения сместится вправо, так как при увеличении T увеличивается vв, которая определяет положение максимума. Но площадь под кривой должна оставаться постоянной. Поэтому величина максимума будет уменьшаться. Влияние же массы молекулы m0 будет обратным. Влияние температуры и массы молекулы на вид функции распределения показано на рис. 6.
Рис. 6. Влияние параметров газа на вид функции распределения
Выражение для средней скорости <v> определяется по формуле:
<v>= vf(v)dv=√(8kT/πm0)=√(8kNAT/πm0NA)=√(8RT/πM) (32)
Аналогично найдем выражение для среднеквадратичной скорости:
<vкв>= v2f(v)dv.
Произведя интегрирование, получим:
<vкв>=√(3RT/M) (33)
Из сравнения найденных скоростей вытекает:
<vкв>=√(3RT/M) > <v>=√(8RT/πM) > vв=√(2RT/M).
Соотношения между скоростями:
vв: <v>: <vкв> = √2: √(8/π): √3 = 1: 1,13: 1,22
При комнатной температуре T=300K средняя арифметическая скорость молекул кислорода будет равна:
<v>=√(8RT/πM)=√(8·8,31·300/π·0,032)≈500 м/с
Первое экспериментальное определение скоростей молекул было осуществлено Штерном в 1920 г: подтвердилась правильность оценки средней скорости молекул, вытекающей из распределения Максвелла; о характере распределения этот опыт дал лишь приближенные сведения. Более точно закон Максвелла был проверен в опыте Ламмерта (1929 г.).
Из функции распределения молекул по модулям скоростей можно получить функцию распределения молекул по кинетическим энергиям теплового движения:
(34)
Найдем среднюю кинетическую энергию <ε> молекулы идеального газа:
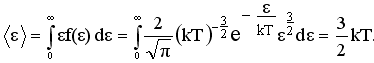
Опыт Штерна — опыт, впервые проведённый немецким физиком Отто Штерном в 1920 году. Опыт являлся одним из первых практических доказательств состоятельности молекулярно-кинетической теории строения вещества. В нём были непосредственно измерены скорости теплового движения молекул и подтверждено наличие распределения молекул газов по скоростям.
Для проведения опыта Штерном был подготовлен прибор, состоящий из двух цилиндров разного радиуса, ось которых совпадала и на ней располагалась платиновая проволока с нанесённым слоем серебра. В пространстве внутри цилиндров посредством непрерывной откачки воздуха поддерживалось достаточно низкое давление. При пропускании электрического тока через проволоку достигалась температура плавления серебра, из-за чего серебро начинало испаряться и атомы серебра летели к внутренней поверхности малого цилиндра равномерно и прямолинейно со скоростью v, определяемой температурой нагрева платиновой проволоки, т. е. температурой плавления серебра. Во внутреннем цилиндре была проделана узкая щель, через которую атомы могли беспрепятственно пролетать далее. Стенки цилиндров специально охлаждались, что способствовало оседанию попадающих на них атомов. В таком состоянии на внутренней поверхности большого цилиндра образовывалась достаточно чёткая узкая полоса серебряного налёта, расположенная прямо напротив щели малого цилиндра. Затем всю систему начинали вращать с некой достаточно большой угловой скоростью ω. При этом полоса налёта смещалась в сторону, противоположную направлению вращения, и теряла чёткость. Измерив смещение s наиболее тёмной части полосы от её положения, когда система покоилась, Штерн определил время полёта, через которое нашёл скорость движения молекул:
где s — смещение полосы, l — расстояние между цилиндрами, а u — скорость движения точек внешнего цилиндра.
Найденная таким образом скорость движения атомов серебра совпала со скоростью, рассчитанной по законам молекулярно-кинетической теории, а тот факт, что получившаяся полоска была размытой, свидетельствовал в пользу того, что скорости атомов различны и распределены по некоторому закону — закону распределения Максвелла: атомы, двигавшиеся быстрее, смещались относительно полосы, полученной в состоянии покоя, на меньшие расстояния, чем те, которые двигались медленнее.
19. Барометрическая формула. Распределение Больцмана. Средне число столкновений и средняя продолжительность свободного пробега молекул.
Барометрическая формула
определяет зависимость давления или плотности газа от высоты в поле тяжести.
Для идеального газа, имеющего постоянную температуру Т и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), Б. ф. имеет следующий вид:
р = p 0exp [- g μ.(h - h0) /RT ] (1),
где р — давление газа в слое, расположенном на высоте h, p0 — давление на нулевом уровне (h = h0), μ — молекулярная масса газа, R —Газовая постоянная, Т — абсолютная температура. Графически зависимость (1) представлена на рис. Из Б. ф. (1) следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону:
n = n0 exp [- mg (h-h0) /kT ],
где m — масса молекулы, k —Больцмана постоянная.
Б. ф. может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см. Больцмана статистика). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на этом, французский физик Ж. Перрен в 1908 применил Б. ф. к распределению по высоте частичек эмульсии, что позволило ему непосредственно определить значение постоянной Больцмана.
Б. ф. показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина — mg (h-h0) /kT, определяющая быстроту спада плотности, представляет собой отношение потенциальной энергии частиц к их средней кинетической энергии, пропорциональной kT. Чем выше температура Т, тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести mg (при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести mg может изменяться за счёт двух величин: ускорения g и массы частиц m.
Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.
Реальное распределение давления и плотности воздуха в земной атмосфере не следует Б. ф., т.к. в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.
Б. ф. лежит в основе барометрического нивелирования — метода определения разности высот Δ h между двумя точками по измеряемому в этих точках давлению (p1 и p2). Поскольку атмосферное давление зависит от погоды, интервал времени между измерениями должен быть возможно меньшим, а пункты измерения располагаться не слишком далеко друг от друга. Б. ф. записывается в этом случае в виде: Δ h = 18400∙ (1+α t) lg (p 1/ p 2) (в м), где t — средняя температура слоя воздуха между точками измерения, α — температурный коэффициент объёмного расширения воздуха. Погрешность при расчётах по этой формуле не превышает 0,1—0,5% от измеряемой высоты. Более точна формула Лапласа, учитывающая влияние влажности воздуха и изменение ускорения свободного падения.
Лит.: Хргиан А. Х., Физика атмосферы, М., 1958.
Ю. Н. Дрожжин.
Падение давления газа с высотой в однородном поле тяжести при постоянной температуре газа (Т1>Т), Пунктирная кривая показывает реальное изменение температуры атмосферы с высотой.
Распределение Больцмана. Запишем барометрическую формулу (2.24) через концентрацию частиц, воспользовавшись тем, что p = nkT:
, (2.25)
где m0 - масса молекулы газа.
Такой же вывод можно провести для любой потенциальной силы (не обязательно для силы тяжести). Из формулы (2.25) видно, что в числителе экспоненты стоит потенциальная энергия одной молекулы в потенциальном поле. Тогда формулу (2.25) можно записать в виде
. (2.26)
В таком виде эта формула пригодна для нахождения концентрации молекул, находящихся в равновесии в поле любой потенциальной силы.
Найдем число частиц газа, координаты которых находятся в элементе объема dV = dxdydz
.
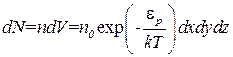Полное число частиц в системе может быть записано в виде
.
Здесь интеграл формально записан по всему пространству, но надо иметь в виду, что объем системы конечен, что приведет к тому, что интегрирование будет вестись по всему объему системы. Тогда отношение
как раз и даст вероятность того, что частица попадет в элемент объема dV. Тогда для этой вероятности запишем
,
где величина потенциальной энергии молекулы будет, вообще говоря, зависеть от всех трех координат. Пользуясь определением функции распределения, можно записать функцию распределения молекул по координатам в следующем виде:
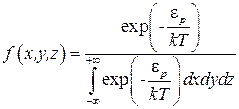. (2.27)
Это и есть функция распределения Больцмана по координатам частиц (или по потенциальным энергиям, имея в виду, что потенциальная энергия зависит от координат). Легко показать, что полученная функция нормирована на единицу.
Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь l, который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с огромным числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул 
.
Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис.68). Он зависит от скорости сталкивающихся молекул, т.е. от температуры газа (несколько уменьшается с ростом температуры).
Рис. 68 Рис. 69
Так как за 1 с молекула проходит в среднем путь, равный средней арифметической скорости 
, и если 
— среднее число столкновений, испытываемых одной молекулой газа за 1 с, то средняя длина свободного пробега
Для определения представим себе молекулу в виде шарика диаметром d, которая движется среди других «застывших» молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d, т. е. лежат внутри «ломаного» цилиндра радиусом d (рис. 69).
Среднее число столкновений за 1 с равно числу молекул в объеме «ломаного» цилиндра: = nV, где n – концентрация молекул, а V = pd2 . Т.е. среднее число столкновений = npd2 .
Расчеты показывают, что при учете движения других молекул
Тогда средняя длина свободного пробега
т.е. обратно пропорциональна концентрации n молекул. С другой стороны, из (42.6) следует, что при постоянной температуре п пропорциональна давлению р. Следовательно,
Условие задачи
Определите среднюю продолжительность τ свободного пробега молекул водорода при температуре 27 С и давлении 0,5 кПа, принимая диаметр молекулы водорода равным 0,28 нм.
Решение задачи
20. Состояние термодинамического равновесия. Параметры состояния. Квазистационарные процессы, их графическое изображение
Состояние термодинамического равновесия является наиболее простым состоянием макроскопической системы. В этом состоянии поведение системы описывается небольшим числом макроскопических параметров. Например, состояние простейших систем – газов, жидкостей и твердых тел при отсутствии внешних силовых полей может быть в условии термодинамического равновесия однозначно определено какими-либо двумя из трех величин Р, Т, V, которые при отсутствии внешних полей имеют одинаковые значения во всех частях системы. Каждое такое равновесное состояние может быть изображено точкой на графике Р-Vили Т-V. Неравновесное состояние не может быть изображено подобным способом, потому что хотя бы один из параметров в неравновесном состоянии не будет иметь определенного значения.
ОПРЕДЕЛЕНИЕ: Термодинамической системой называется совокупность тел, обменивающихся энергией, как друг с другом, так и с окружающими телами.
Примером системы может служить жидкость и находящийся в равновесии с ней пар. Система может состоять и из одного тела: жидкость, газ, твердое тело.
Всякая система может находиться в различных состояниях, отличающихся температурой, давлением, объемом и т.д.
ОПРЕДЕЛЕНИЕ: Совокупность физических величин, однозначно определяющих состояние системы, называется параметрами системы.
Не всегда какой-либо параметр имеет определенное значение. Если, например, температура в разных точках тела неодинакова, то телу нельзя приписать определенное значение параметра “T”. В этом случае состояние называется неравновесным. Если такое тело изолировать от других тел и предоставить самому себе, то температура выровняется и примет одинаковое для всех точек значение “T” – тело перейдет в равновесное состояние. Это значение температуры не изменится до тех пор, пока тело не будет выведено из равновесного состояния воздействием извне.
То же самое может иметь место и для других параметров системы, например для давления “p”.
А что же будем называть равновесным состоянием?
ОПРЕДЕЛЕНИЕ: Равновесным состоянием системы будем называть такое состояние, при котором все параметры системы имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Если по координатным осям откладывать значения каких-либо 2 х параметров, то любое равновесное состояние может быть изображено точкой на этом графике (например, точкой 1). Неравновесное состояние не может быть изображено таким способом, т.к. в неравновесном состоянии хотя бы один из параметров не имеет определенного значения.
Процесс перехода системы из неравновесного состояния в равновесное называется процессом релаксации. Время, затрачиваемое на такой переход, называют временем релаксации. В качестве времени релаксации принимается время, за которое первоначальное отклонение какой-либо величины от равновесного значения уменьшается в “e” раз. Для каждого параметра имеется свое время релаксации. Наибольшее из этих времен играет роль времени релаксации системы.
Всякий процесс, т.е. переход системы из одного состояния в другое связан с нарушением равновесия системы. Следовательно, при протекании в системе какого-либо процесса она проходит через последовательность неравновесных состояний. В предельном случае бесконечно медленный процесс будет состоять из последовательности равновесных состояний.
ОПРЕДЕЛЕНИЕ: Процесс, состоящий из последовательности равновесных состояний, будет называться равновесным (равновесный процесс – абстракция).
Равновесный процесс может быть изображен на графике соответствующей сплошной кривой. Неравновесные процессы будем условно изображать пунктирными линиями.
Равновесный процесс может быть проведен в обратном направлении, причем система будет проходить через те же состояния, что и при прямом ходе, но в обратной последовательности. Поэтому равновесные процессы также называются обратимыми.
Понятия равновесного состояния и обратимого процесса играют большую роль в термодинамике. Все количественные выводы термодинамики строго применимы только к равновесным состояниям и обратимым процессам.
Квазистационарный процесс
процесс, протекающий в ограниченной системе ираспространяющийся в ней так быстро, что за время распространения этого процесса в пределах системыеё состояние не успевает измениться. Поэтому при рассмотрении процесса можно пренебречь временем егораспространения в пределах системы. Например, если в каком-либо участке замкнутой электрической цепидействует переменная внешняя эдс, но время распространения электромагнитного поля до наиболееудалённых точек цепи столь мало, что величина эдс не успевает сколько-нибудь заметно изменяться за этовремя, то изменения напряжений и токов в цепи можно рассматривать как К. п. В этом случае переменныеэлектрические и магнитные поля, создаваемые движущимися в цепи электрическими зарядами(распределение и скорости которых изменяются со временем), оказываются в каждый момент временитакими же, какими были бы стационарные электрические и магнитные поля (поля стационарных зарядов итоков), распределение и скорости которых (не изменяющиеся со временем) совпадают с распределением искоростями зарядов, существующими в системе в рассматриваемый момент времени. Однако в случаенестационарных токов наряду с электрическими полями зарядов возникают вихревые электрические поля, обусловленные изменениями магнитных полей. Действие этих полей может быть учтено путём введения эдсиндукции (наряду со сторонними эдс источников). Но введение эдс индукции не нарушает основной чертыстационарных токов — равенства сил токов во всех сечениях неразветвлённой цепи. В силу этого дляэлектрических цепей, удовлетворяющих условиям квазистационарности (квазистационарных токов (См. Квазистационарный ток)), справедливы Кирхгофа правила.Условия квазистационарности наиболее простоформулируются для случая периодических процессов. Процессы можно считать квазистационарными вслучае, если время распространения между наиболее удалёнными друг от друга точками рассматриваемойсистемы мало по сравнению с периодом процесса или, что то же самое, когда расстояние между указаннымиточками мало по сравнению с соответствующей длиной волны.
Понятие К. п. может быть применено и к др. системам — механическим, термодинамическим. Если, например, на один из концов упругого стержня действует переменная внешняя сила, направленная вдольстержня, и если условие квазистационарности выполняется, т. е. за время распространения продольнойупругой волны от одного конца стержня до другого величина силы не успевает измениться, то ускорения всехточек стержня в каждый момент времени определяются значением силы в этот же момент времени. Процесстеплопроводности (См. Теплопроводность) можно считать К. п., если выравнивание температуры втеплопроводящем стержне происходит значительно быстрее, чем изменение внешних условий: температур T 1 и T 2 концов стержня.
21. Градиент Физической величины. Диффузия. Закон Фика
Градиентом физической величины называется отношение приращения этой функции к расстоянию, на котором это приращение происходит. Градиент физической величины – величина векторная и направлена в сторону увеличения значений этой величины.
grad T
● ●
T1 ΔX T2
Т1>Т2
Физической величиной называют все то, что можно измерить количественно. Физические величины бывают векторные и скалярные.
Векторные величины, кроме численного значения, имеют еще и направление. Скалярные величины имеют только численные значения.
Для получения числовых значений физических величин необходимо измерять эти физические величины. Измерение физической величины сводится к сравнению её с однородной физической величиной, принятой за единицу. Для каждой физической величины эту единицу можно выбирать произвольно. Однако на практике для удобства выбраны единицы только для семи физических величин, называемых основными. Единицы всех остальных физических величин устанавливают на основании законов, связывающих эти величины с основными. Совокупность всех единиц измерения физических величин называется системой единиц.
Диффузия (закон Фика)
В предыдущих параграфах были рассмотрены характерные черты молекулярно-теплового движения, тепловое равновесие и процессы, происходящие, когда тепловое равновесие нарушено (излучение, теплопроводность и конвекция). Все это еще не дает, однако, полного представления о молекулярно-тепловом движении. Мы должны обратиться к явлению диффузии — к явлению, которое обязывает нас перейти от понятия теплового равновесия к понятию термодинамического равновесия.
Диффузией называется обусловленный хаотическим движением молекул процесс постепенного взаимного проникновения двух веществ, граничащих друг с другом. Один из первых опытов по исследованию диффузии был сделан немецким физиком Лошмидтом. Он взял две стеклянные трубки, закрытые с одного конца, имевшие в длину около полметра, в диаметре 2,5 см; одну трубку он наполнил углекислым газом, а другую — водородом и поместил их в вертикальном положении так, что открытые концы трубок соприкасались; При этом трубка с углекислым газом была внизу (последнее было необходимо для того, чтобы смешение обоих газов происходило лишь вследствие молекулярных движений, а не вследствие различной тяжести этих газов). Содержимое трубок было исследовано через полчаса; оказалось, что в верхнюю трубку проникло из нижней 37% углекислого газа.
Если бы молекулы газа вообще не сталкивались, то благодаря своим большим скоростям они уже за малую часть секунды пробегали бы значительные расстояния по прямой линии. Поэтому процесс смешения двух газов, соприкасающихся друг с другом, шел бы чрезвычайно быстро. Опыт Лошмидта показывает, что в действительности диффузия газа происходит не особенно быстро. Это видно уже из обыденных явлений: например, если в одном углу комнаты
открытфлакон с духами и если воздух в комнате находится в макроскопическом покое, то пройдет немало времени, прежде чем мы почувствуем появление запаха духов в противоположном углу комнаты.
Сравнительная медленность процесса диффузии является результатом молекулярных столкновений, вследствие которых молекула может быть отброшена назад в ту сторону, откуда она пришла. Мы знаем, что в результате столкновений молекула описывает чрезвычайно запутанную зигзагообразную траекторию; за 1 сек. она пройдет по этой траектории несколько сот метров и все-таки может находиться очень недале