ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 19
По дисциплине: ЭЛЕМЕНТЫВЫСШЕЙ МАТЕМАТИКИ
Наименование работы: ПЕРЕВОД КОМПЛЕКСНЫХ ЧИСЕЛ ИЗ ОДНОЙ ФОРМЫЗАПИСИ В ДРУГУЮ.
Для специальности 230111, 230115.
Составлено преподавателем Калмыковой О.И.
г. Смоленск
2012 г.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 19
По дисциплине: ЭЛЕМЕНТЫВЫСШЕЙ МАТЕМАТИКИ (2 курс)
Наименование работы: ПЕРЕВОД КОМПЛЕКСНЫХ ЧИСЕЛ ИЗ ОДНОЙ ФОРМЫЗАПИСИ В ДРУГУЮ.
1. Цель работы: Приобретение навыков записи комплексного числа в трех различных формах, перевод чисел из одной формы записи в другую.
2. Литература:
2.1. Богомолов Н.В. Практические занятия по математике: М.; Высшая школа, 1990.
3. Подготовка к работе:
3.1. Изучить теоретический материал по теме “Комплексные числа”
3.2. Подготовить бланки отчета.
3.3. Подготовить ответы на вопросы допуска к работе.
4. Основное оборудование:
4.1. Литература, конспект.
5. Задание:
5.1. Указать модуль и аргумент заданных комплексных чисел.
5.2. Записать комплексных числа в двух недостающих формах.
6. Порядок выполнения работы: 
6.1. Записать задание своего варианта в отчет.
6.2. Выполнить задание своего варианта.
6.3. Выполнить дополнительное задание.
6.4. Записать ответы, оформить отчет
6.5. Подготовить ответы на контрольные вопросы.
7. Содержание отчета:
7.1. Титульный лист.
7.2. Цель работы.
7.3. Результаты и ход выполнения работы.
7.4. Выводы отчеты.
8. Контрольные вопросы:
8.1. Дать понятие модуля комплексного числа, формула его вычисления.
8.2. Понятие аргумента комплексного числа, формула его вычисления.
8.3. Три формы записи комплексного числа.
8.4. Основное свойство мнимой единицы.
8.5. Геометрическая интерпретация комплексного числа.
9. Приложение:
|
Вариант1
1. 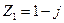
2. 
3. 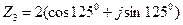
4. 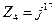
Вариант2
1. 
2. 
3. 
4. 
Вариант3 Вариант6
1.  1.
1. 
2. 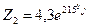 2.
2. 
3.  3.
3. 
4. 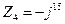 4.
4. 
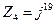
10. Методические указания:
Определение. Комплексным числом z называется выражение  , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:
, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:

При этом число a называется действительной частью числа z (a = Re z), а b - мнимой частью (b = Im z).
Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.
Определение. Числа  и
и  называются комплексно – сопряженными.
называются комплексно – сопряженными.
Определение. Два комплексных числа  и
и  называются равными, если соответственно равны их действительные и мнимые части:
называются равными, если соответственно равны их действительные и мнимые части:

Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.

Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.
 |
у
A(a, b)
r
j b
0 a x
Таким образом, на оси ОХ располагаются действительные числа, а на оси ОY – чисто мнимые.
С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.
Тригонометрическая форма числа.
Из геометрических соображений видно, что  . Тогда комплексное число можно представить в виде:
. Тогда комплексное число можно представить в виде:


Такая форма записи называется тригонометрической формой записи комплексного числа.
При этом величина r называется модулем комплексного числа, а угол наклона j - аргументом комплексного числа.
 .
.
Из геометрических соображений видно:

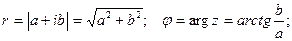
Очевидно, что комплексно – сопряженные числа имеют одинаковые модули и противоположные аргументы.

Действия с комплексными числами.
Основные действия с комплексными числами вытекают из действий с многочленами.
1) Сложение и вычитание.



2) Умножение.
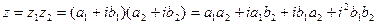


В тригонометрической форме:
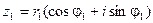 ,
, 


С случае комплексно – сопряженных чисел:

3) Деление.
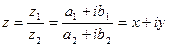
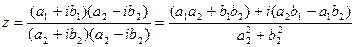


В тригонометрической форме:


4) Возведение в степень.
Из операции умножения комплексных чисел следует, что

В общем случае получим:


где n – целое положительное число.
Это выражение называется формулой Муавра.
(Абрахам де Муавр (1667 – 1754) – английский математик)
Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов.
Пример. Найти формулы sin2j и cos2j.
Рассмотрим некоторое комплексное число 
Тогда с одной стороны  .
.
По формуле Муавра: 
Приравнивая, получим 
Т.к. два комплексных числа равны, если равны их действительные и мнимые части, то
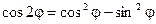

Получили известные формулы двойного угла.
5) Извлечение корня из комплексного числа.

Возводя в степень, получим:

Отсюда: 


Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.
Показательная форма комплексного числа.
Рассмотрим показательную функцию 
Можно показать, что функция w может быть записана в виде:


Данное равенство называется уравнением Эйлера. Вывод этого уравнения будет рассмотрен позднее.
Для комплексных чисел будут справедливы следующие свойства:
1) 
2) 
3)  где m – целое число.
где m – целое число.
Если в уравнении Эйлера показатель степени принять за чисто мнимое число (х=0), то получаем:

Для комплексно – сопряженного числа получаем:

Из этих двух уравнений получаем:


Этими формулами пользуются для нахождения значений степеней тригонометрических функций через функции кратных углов.
Если представить комплексное число в тригонометрической форме:

и воспользуемся формулой Эйлера: 


Полученное равенство и есть показательная форма комплексного числа.
Пример. Даны два комплексных числа 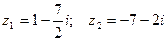 . Требуется а) найти значение выражения
. Требуется а) найти значение выражения 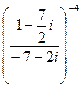 в алгебраической форме, б) для числа
в алгебраической форме, б) для числа  найти тригонометрическую форму, в) найти z20.
найти тригонометрическую форму, в) найти z20.
a) Очевидно, справедливо следующее преобразование:

Далее производим деление двух комплексных чисел:

Получаем значение заданного выражения: 16(- i)4 = 16 i 4 =16.
б) Число  представим в виде
представим в виде  , где
, где

Тогда 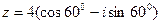 .
.
в) Для нахождения 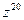 воспользуемся формулой Муавра.
воспользуемся формулой Муавра.


 2.
2.  3.
3.  4.
4.  Вариант5
1.
Вариант5
1.  2.
2.  3.
3.  4.
4. 