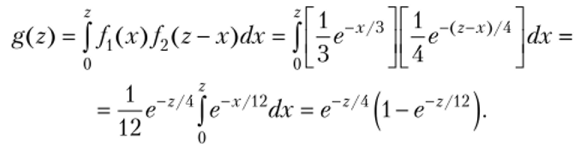Если каждой паре возможных значений случайных величин X и Усоответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и У:
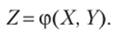
Далее на примерах будет показано, как найти распределение функции Z = X + У по известным распределениям слагаемых. Такая задача часто встречается на практике. Например, если X — погрешность показаний измерительного прибора (распределена нормально), У — погрешность округления показаний до ближайшего деления шкалы (распределена равномерно), то возникает задача — найти закон распределения суммы погрешностей Z = Х+ У.
1. ПустьХи У — дискретные независимые случайные величин ы. Для того чтобы составить закон распределения функции Z = X + У, надо найти все возможные значения Z и их вероятности.
Пример 1. Дискретные независимые случайные величины заданы распределениями:

Составить распределение случайной величины Z=X+ У.
Решение. Возможные значения Z есть суммы каждого возможного значения X со всеми возможными значениями У:
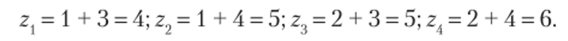
Найдем вероятности этих возможных значений. Для того чтобы Z= 4, достаточно, чтобы величина X приняла значение х = 1 и величина У — значение у = 3. Вероятности этих возможных значений, как следует из данных законов распределения, соответственно равны 0,4 и 0,2.
Аргументы X и Унезависимы, поэтому события Х= 1 и У=3 независимы и, следовательно, вероятность их совместного наступления (т.е. вероятность события Z= 1 + 3 = 4) по теореме умножения равна 0,4 • 0,2 = 0,08.
Аналогично найдем: 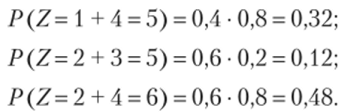
Напишем искомое распределение, сложив предварительно вероятности несовместных событий Z=z2,Z=z3 (0,32 + 0,12 = 0,44):
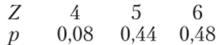
Контроль: 0,08 + 0,44 + 0,48 = 1.
2.Пусть Хи Y— непрерывные случайные величины. Доказано: если X и Y независимы, то плотность распределения g(z) суммы Z=X+ Y (при условии, что плотность хотя бы одного из аргументов задана на интервале одной формулой) может быть найдена с помощью равенства
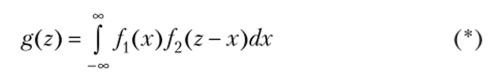
либо с помощью равносильного равенства
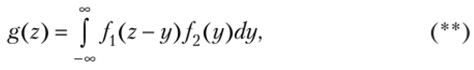
где/j,/2 — плотности распределения аргументов.
Если возможные значения аргументов неотрицательны, то g(z) находят по формуле
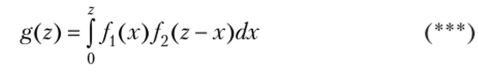
либо по равносильной формуле
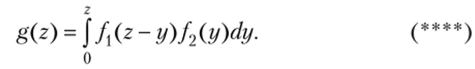
Плотность распределения суммы независимых случайных величин называют композицией.
Закон распределения вероятностей называют устойчивым, если композиция таких законов есть тот же закон (отличающийся, вообще говоря, параметрами). Нормальный закон обладает свойством устойчивости: композиция нормальных законов также имеет нормальное распределение (математическое ожидание и дисперсия этой композиции равны соответственно суммам математических ожиданий и дисперсий слагаемых). Например, если X и V — независимые случайные величины, распределенные нормально с математическими ожиданиями и дисперсиями, соответственно равными ал = 3, а2 = 4, Dx = 1, D2 = 0,3, то композиция этих величин, т.е. плотность вероятности суммы Z = X + Iтакже распределена нормально.
Пример 2. Независимые случайные величины X и Y заданы плотностями распределений:
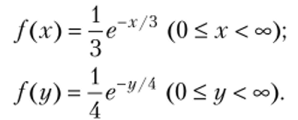
Найти композицию этих законов, т.е. плотность распределения случайной величины
Z=X + Y.
Р е ш е н и е. Возможные значения аргументов неотрицательны, поэтому воспользуемся формулой (***)