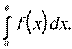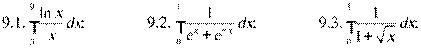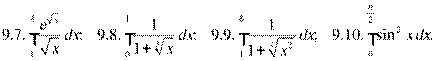Составными элементами структуры контрольной работы являются: титульный лист, основная часть, список использованных источников.
ОСНОВНАЯ ЧАСТЬ
К выполнению самостоятельного задания следует приступать после изучения учебной литературы и материалов лекций. Правильно выполненная контрольная работа является условием допуска студента к экзамену.
При выполнении контрольной работы необходимо руководствоваться следующим:
1. Контрольная работа должна быть выполнена строго по своему варианту, который определяется по последней цифре номера зачетной книжки студента и указывается на титульном листе.
2. Условия задач должны быть обязательно переписаны.
3. Решения задач должны сопровождаться развернутыми пояснениями по ходу решения задачи, с указанием формул, по которым производится расчет.
5. Студент должен выполнить все задачи, входящие в его вариант.
Работа должна быть выполнена в отдельной тетради или на бумаге формата А4 с оформлением титульного листа.
6. Внешнее оформление работы должно соответствовать предъявляемым требованиям.
7. В конце работы следует указать использованную литературу (автора, название и год издания).
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Общий список использованных источников должен содержать не менее 10 наименований.
Не менее 50%использованныхисточников обязательно должны быть упомянуты в тексте контрольной работы, т.е. по тексту работы должны быть оформлены ссылки на используемые источники.
ПЕРЕЧЕНЬ РЕКОМЕНДУЕМЫХ ИСТОЧНИКОВ ДЛЯ ПОДГОТОВКИ
КОНТРОЛЬНОЙ РАБОТЫ
1. И.Ш.Кремер Высшая математика для экономического бакалавриа-та: учебник и практикум/ М.: Изд-во ЮРАЙТ, 2013 (ЭБ РТА)
2. Гмурман, В. Е. Теория вероятностей и математическая статистика: учебник для прикладного бакалавриата / В. Е. Гмурман. - М.: Юрайт, 2014 (ЭБ РТА).
3. Вафодорова Г.О. Практикум по дисциплине «Математика» / О. Вафодорова, С.В. Суржик, Н.В. Ширкунова. М.: Изд-во Российской тамо-женной академии, 2012. 174 с. (ЭБ РТА)
4. Ширкунова Н.В. Математика: курс лекций. В 2 ч. Ч. 1 - М.: Изд-во Российской таможенной академии. 2014. (ЭБ РТА)
5. Ширкунова Н.В. Математика: курс лекций. В 2 ч. Ч. 2. - М.: Изд-во Российской таможенной академии. 2014. (ЭБ РТА)
4. ПЕРЕЧЕНЬ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ
ПО ДИСЦИПЛИНЕ
1 семестр
1.1. – 1.10. Даны вершины треугольника: А(х1, у1), В(х2, у2), С(х3, у3). Требуется найти: 1) уравнения всех сторон; 2) уравнение медианы СМ и ее длину; 3) уравнение высоты СН и ее длину; 4) внутренние углы треугольника; 5) сделать чертеж.
– 1.1. А(1; 1); В(7; 4); С(4; 5).
1.2. А1; 1); В(–5; 4); С(–2; 5).
1.3. А(–1; 1); В(5; 4); С(2; 5).
1.4. А(–1; 1); В(–7; 4); С(–4; 5).
1.5. А(1; –1); В(7; 2); С(4; 5).
1.6. А(1; –1); В(–5; 2); С(–2; 3).
1.7. А(–1; –1); В(5; 2); С(2; 3).
1.8. А(–1; –1); В(–7; 2); С(–4; 3);
1.9. А(0; 1); В(6; 4); С(3; 5).
1.10. А(1; 0); В(7; 3); С(4; 4).
2.1. Составить уравнение линии, расстояния каждой точки которой от начала координат и от точки А(5; 0) относятся как 2: 1. Сделать чертеж.
2.2. Составить уравнение линии, для каждой точки которой ее расстояние до точки F(– 1; – 2) равно расстоянию от прямой х = – 3. Сделать чертеж.
2.3. Составить уравнение линии, расстояние каждой точки которой от точки А(– 1; 0) вдвое меньше расстояния ее от прямой х = – 4. Сделать чертеж.
2.4. Составить уравнение линии, для каждой точки которой отношение расстояний до точки F(7; 0) и прямой х = 1 равно 
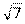 . Сделать чертеж.
. Сделать чертеж.
2.5. Составить уравнение линии, расстояния каждой точки которой от точки А(2; 0) и от прямой 5х + 8 = 0 относятся как 5: 4. Сделать чертеж.
2.6. Составить уравнение линии, для каждой точки которой отношение расстояний до точки F(2; 0) и прямой х = 3 равно 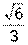
 . Сделать чертеж.
. Сделать чертеж.
2. 7. Составить уравнение линии, каждая точка которой находится вдвое дальше от точки А(4; 0), чем от точки В(1; 0). Сделать чертеж.
2.8. Составить уравнение линии, для каждой точки которой ее расстояние до точки F(3; 3) равно расстоянию от прямой у = – 2. Сделать чертеж.
2.9. Составить уравнение линии, расстояния каждой точки которой от точки А(2; 0) и от прямой 2х + 5 = 0 относятся как 4: 5.
2.10. Составить уравнение линии, для каждой точки которой отношение расстояний до точки F(2; 0) и прямой 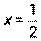 равно 2. Сделать чертеж.
равно 2. Сделать чертеж.
3.1 – 3.10. Найти пределы функций
3.1. 1)  при а) х0 = 3, б) х0 = ∞; 2)
при а) х0 = 3, б) х0 = ∞; 2) 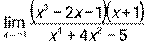 ;
;
3)  4)
4)  5)
5) 
3.2. 1) 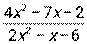 при а) х0 = 2, б) х0 = ∞; 2)
при а) х0 = 2, б) х0 = ∞; 2) 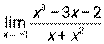 ;
;
3) 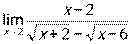 ; 4)
; 4) 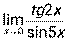 ; 5)
; 5)  .
.
3.3. 1) 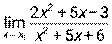 при а) х0 = – 3, б) х0 = ∞; 2)
при а) х0 = – 3, б) х0 = ∞; 2) 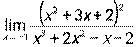 ;
;
3) 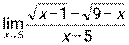 ; 4)
; 4) 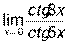 ; 5)
; 5) 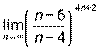 .
.
3.4. 1)  при а) х0 = – 2, б) х0 = ∞; 2)
при а) х0 = – 2, б) х0 = ∞; 2) 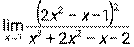 ;
;
3) 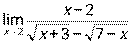 ; 4)
; 4) 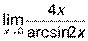 ; 5)
; 5)  .
.
3.5. 1) 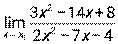 при а) х0 = 4, б) х0 = ∞; 2)
при а) х0 = 4, б) х0 = ∞; 2)  ;
;
3)  ; 4)
; 4)  ; 5)
; 5) 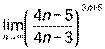 .
.
3.6. 1)  при а) х0 = 5, б) х0 = ∞; 2)
при а) х0 = 5, б) х0 = ∞; 2) 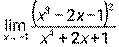 ;
;
3) 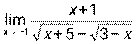 ; 4)
; 4) 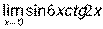 ; 5)
; 5)  .
.
3.7. 1)  при а) х0 = – 4, б) х0 = ∞; 2)
при а) х0 = – 4, б) х0 = ∞; 2) 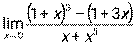 ;
;
3) 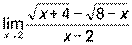 ; 4)
; 4) 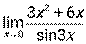 ; 5)
; 5) 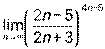 .
.
3.8. 1)  при а) х0 = – 5, б) х0 = ∞; 2)
при а) х0 = – 5, б) х0 = ∞; 2) 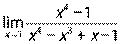 ;
;
3) 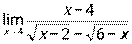 ; 4)
; 4) 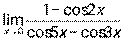 ; 5)
; 5)  .
.
3.9. 1) 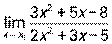 при а) х0 = 1, б) х0 = ∞; 2)
при а) х0 = 1, б) х0 = ∞; 2) 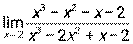 ;
;
3)  ; 4)
; 4) 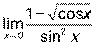 ; 5)
; 5) 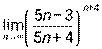 .
.
3.10. 1) 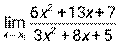 при а) х0 = – 1, б) х0 = ∞; 2)
при а) х0 = – 1, б) х0 = ∞; 2) 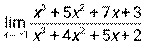 ;
;
3) 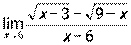 ; 4)
; 4) 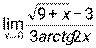 ; 5)
; 5)  .
.
4.1 – 4.10. Дана функция y = f(x). Требуется исследовать ее на непрерывность, найти точки разрыва, если они есть, и установить характер разрыва.
4. 1. 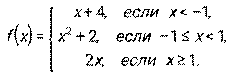 4.2.
4.2. 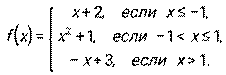
4.3. 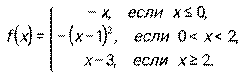 4. 4.
4. 4. 
4. 5. 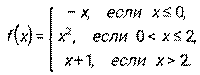 4.6.
4.6. 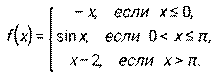
4.7.  4.8.
4.8. 
4.9. 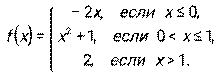 4.10.
4.10. 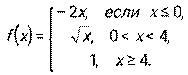
5.1-5.10. Найти производную функции:
5.1. 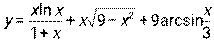 . 5.2
. 5.2 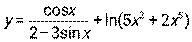 .
.
5.3. 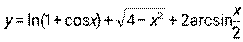 . 5.4
. 5.4  .
.
5.5. 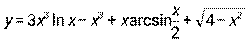 . 5.6.
. 5.6.  .
.
5.7. 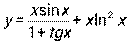 . 5.8.
. 5.8.  .
.
5.9.  . 5.10.
. 5.10.  .
.
6.1-6.10. Проведите полное исследование функции и постройте ее график.
6.1  6.2
6.2 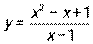 6.3
6.3 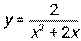 6.4
6.4 
6.5 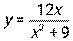 6.6
6.6 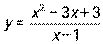 6.7
6.7 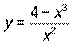
6.8  6.9
6.9 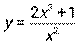 6.10
6.10 
7.1 - 7.10. Найти полный дифференциал функции 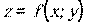 .
.
7.1. 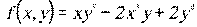 7.2.
7.2. 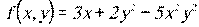
7.3. 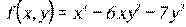 7.4.
7.4. 
7.5. 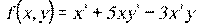 7.6.
7.6. 
7.7. 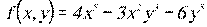 7.8.
7.8. 
7.9.  7.10.
7.10. 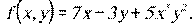
8.1-8.10 Найти неопределенные интегралы. Результаты проверить дифференцированием.
8.1. 

8.2. 

8.3. 


8.4. 

8.5. 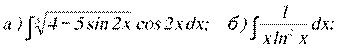

8.6. 


8.7. 

8.8. 

8.9. 

8.10. 

9.1-9.10 Вычислить по формуле Ньютона-Лейбница определенный интеграл