Примеры ключевых задач по геометрии при подготовке к ОГЭ
Свойства хорд и дуг окружности
· Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
· Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
· Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
· Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
· У равных дуг равны и хорды.
· Дуги, заключённые между параллельными хордами, равны.
Свойства касательной к окружности
· Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
· Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Теоремы о длинах хорд, касательных и секущих
· Произведения длин отрезков, на которые разбита каждая из хорд, равны:
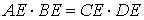
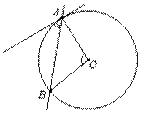
· Если из точки, взятой вне окружности, проведены к окружности секущая и касательная, то произведение секущей на её внешнюю часть равно квадрату касательной.
· Если из точки, взятой вне окружности, проведены к окружности секущие, то произведение каждой секущей на её внешнюю часть есть число постоянное для всех этих секущих
Угол между хордой и касательной
Угол, образованный хордой и касательной, имеющими общую точку на окружности, равен половине дуги, заключенной между его сторонами.
Свойства вписанного угла окружности.
· Вписанный угол измеряется половиной дуги, на которую он опирается.
· Вписанные углы, опирающиеся на одну и ту же дугу, равны.
|
|
· Вписанный угол, опирающийся на полуокружность (диаметр) – прямой.
· Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от хорды.
· Вписанные углы, опирающиеся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от хорды.
Свойства биссектрисы угла треугольника
Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
Свойства биссектрисы параллелограмма
· Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
· Биссектрисы углов параллелограмма, прилежащих к одной стороне, перпендикулярны
Свойства прямоугольного треугольника
· В прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
· Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы.
· Если в треугольнике медиана равна половине длины стороны, к которой она проведена, то этот треугольник – прямоугольный.
· В прямоугольном треугольнике радиус вписанной окружности вычисляется по формуле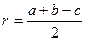 
, где a, b – катеты, c –гипотенуза прямоугольного треугольника АВС.
Свойства медианы треугольника
· В треугольнике медианы пересекаются в одной точки и делятся этой точкой в отношении 2:1, считая от вершины.
· Медиана делит треугольник на два равновеликих треугольника, а три медианы – на шесть равновеликих треугольников.
· Если О – точка пересечения медиан треугольника АВС, то S(ABC) = 3S(AOB) = 3S(AOC) = 3S(BOC).
|
|
Свойства элементов трапеции
Во всякой трапеции:
• Середины боковых сторон и середины диагоналей лежат на одной прямой
• Средняя линия трапеции равна полусумме оснований; отрезок, соединяющий середины диагоналей, равен полуразности оснований
• Во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой
• Любой отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в отношении OX:OY=BC:AD
• Биссектриса угла трапеции отсекает от нее равнобедренный треугольник
• Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны и точка их пересечения лежит на средней линии трапеции
В описанной около окружности трапеции:
• Сумма оснований равна сумме боковых сторон
• Полусумма боковых сторон равна средней линии
• Если трапеция равнобедренная, то ее боковая сторона равна средней линии, высота трапеции равна среднему геометрическому ее оснований
• Отрезки, соединяющие центр окружности, вписанной в трапецию, с вершинами трапеции, попарно перпендикулярны
• Диаметр вписанной в трапецию окружности является высотой трапеции
• Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой – их полусумме, т.е. равен средней линии трапеции.
1) S(ABC)=S(DBC)
2) S(ABD)=S(ACD)
3) S(ABO)=S(COD)
• Средняя линия и высота равнобедренной трапеции с взаимно перпендикулярными диагоналями равны.