Тема 1. Основы вакуумной техники
Основы физики вакуума (равновесная газовая среда)
Распределение Максвелла
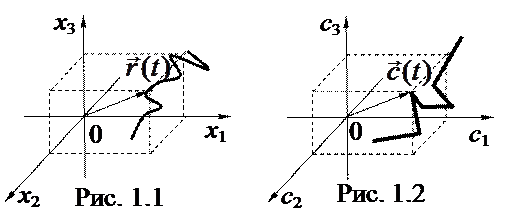
|

| (1.1) |
где

| (1.2) |
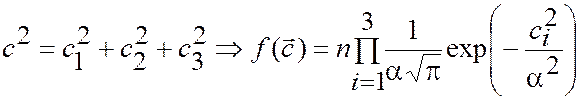
| |

| (1.3) |
где

| (1.4) |
Распределения частиц по скоростям и энергиям
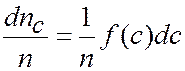
| (1.5) |

| (1.6) |


|
 . .
| (1.7) |
где
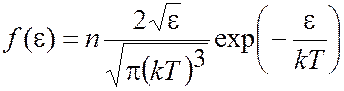 . .
| (1.8) |
Макроскопические характеристики газовой среды

| (1.9) |

| (1.10) |

| (1.11) |

| (1.12) |

| (1.13) |

|
Для N 2 при T = 273 K: 402, 453 и 492 м/с.
Потоки в газе
Плотность величины А → An
Плотность потока величины А → 
| Таблица 1 | |||
| Характеристика газовой среды | Физическая величина | ||
Масса
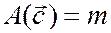
| Импульс

| Энергия

| |
| Плотность | r = nm | 
| 
|
| Плотность потока | 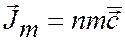
| 
| 
|
1. Перенос массы (плотность потока массы)

|
 |

| (1.14) |
Поток газа на стенку в м–3/c: для атм. воздуха при T = 298 К и p = 105 Па
n = 2.7×1025 м–3,  » 450 м/с
» 450 м/с
J w = 3.0×1027 м–2×с–1, V w» 110 м3/(м2×с).
2. Перенос энергии
Средняя энергия частицы
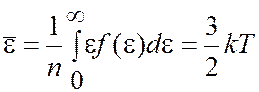
| (1.15) |
Плотность потока энергии

|
3. Перенос импульса (плотность потока импульса)

| (1.16) |
 |
 , ,
|

| (1.17) |

| (1.18) |
| P = 1/3(P 1 + P 2 + P 3) = nkT | (1.19) |
Распределение Больцмана

| (1.20) |
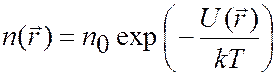
| (1.21) |

| (1.22) |

| (1.23) |
Распределение Максвелла–Больцмана


| (1.24) |

| (1.25) |

| (1.26) |

| (1.27) |
Средняя длина свободного пробега частицы

| (1.28) |
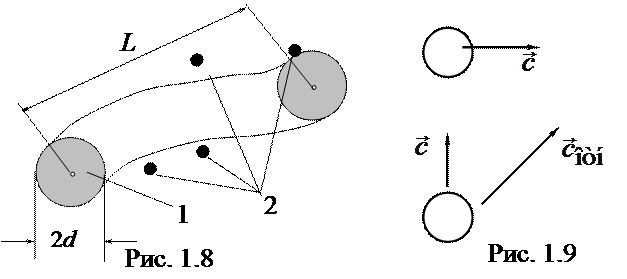
|

| |

| (1.29) |

| (1.30) |

| |

| (1.31) |
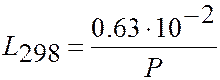
| (1.32) |

| (1.33) |
| Степени вакуума | Kn | |
| Низкий | «1 | |
| Средний | ≈ 1 | |
| Высокий | » 1 | |
| Сверхвысокий | » 1, θ < R 0 | |
Вязкость (перенос импульса)
 |

| (1.34) |
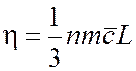
| (1.35) |
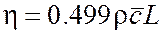
| (1.36) |
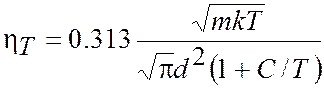
| (1.37) |
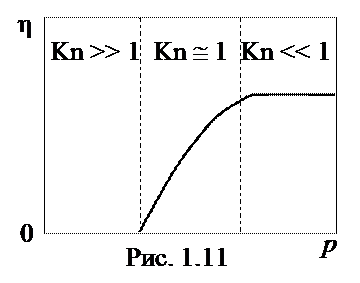
|
Теплопроводность (перенос энергии)

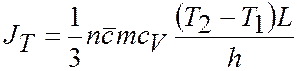
| (1.38) |
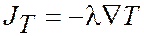
| (1.39) |

| (1.40) |

| (1.41) |

| (1.42) |
Диффузия (перенос массы)

| (1.43) |

| (1.44) |
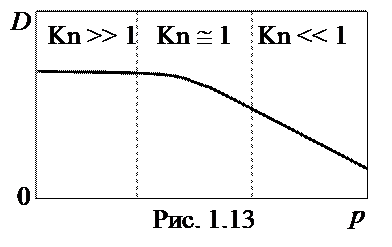
|

| (1.45) |
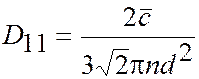
| |

|
Режимы течения газа
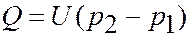 , м3 Па/c , м3 Па/c
| (1.46) |
  , м3/c , м3/c
|
Поток может носить вязкостный (ламинарный), молекулярный или промежуточный характер. Критерий Kn:
| Степени вакуума | Kn |
| Низкий | «1 |
| Средний | ≈ 1 |
| Высокий | » 1 |
Проводимость элементов вакуумной системы
 |
1.3.1. Вязкостный режим
Уравнение Пуазейля:.
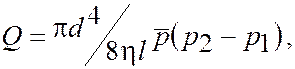
| (1.47) |

| (1.48) |

| (1.49) |
Для воздуха.
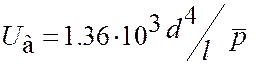
| (1.50) |
Молекулярный режим

| (1.51) |

| (1.52) |
При A (x) =const, H (x) = const

| (1.53) |
Для цилиндрическойтрубы

| (1.54) |
Промежуточный режим

| (1.55) |
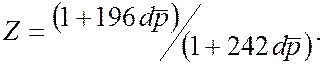
| (1.56) |
 |
1.4. Основное уравнение вакуумной техники
 |
| S 0 = dV 1/ dt = Q / p 1,м3/с | (1.57) |
| S эф = dV 2/ dt = Q / p 2,м3/с | (1.58) |
| 1/ S эф – 1/ S 0 = 1/ U | (1.59) |
| S эф < S 0 |
Откачка вакуумного объема
 |
| d (pV)/ dt = Q вх – Q вых | (1.60) |
| Vdp/dt = Q вх– S эф p 2. | (1.61) |
Начальное условие. p (0) = p 0:

| (1.62) |

| (1.63) |
Вакуумные насосы
По назначению:
– низковакуумные (102…104) Па;
– среднего вакуума (10-1…102) Па;
– высоковакуумные (10-10…10-1) Па.
По принципу действия:
– механические (объемные и молекулярные);
– струйные;
– электрофизические;
– сорбционные.
Основные параметры:
 |
– номинальная быстрота действия S 0;
– предельное давление p пр;
– наимененьшее рабочее давление p мин, при котором S = S 0;
– наибольшее рабочее давление p макс, при котором S = S 0;
– давление запуска p зап;
– наибольшее выпускное давление p вып
– эффективная быстрота действия S эф
– коэффициент использования:

| (1.64) |
– производительность насоса:

| (1.65) |
Объемная откачка
Удаление газа из вакуумной камеры за счет циклического изменения объема камеры насоса.
цикл I (0– t 1) – объем камеры увеличивается, всасывание в нее газа, давление сохраняется на уровне минимального значения p пр;
цикл II (t 1 – t 2) – объем камеры уменьшается, сжатие газа, давление возрастает до атмосферного p а;
цикл III (t 2– t 3) – выброс газа в атмосферу. За полный оборот ротора в каждой из двух камер происходят все три цикла.

|
|
Молекулярная откачка
 |
Удаление газа из вакуумной камеры с помощью движущейся поверхности.
Условия:
– u ст >  ;
;
– малые зазоры (менее 0.1 мм), чтобы уменьшить обратное перетекание газа;
– молекулярный режим течения газа в канале
Предельное давление:

| (1.66) |
где U к – проводимость канала ~  ; S max – максимальная быстрота действия ~ u ст.
; S max – максимальная быстрота действия ~ u ст.
Для понижения p пр: T ↓, u ст ↑, p 1↓
 |

Другой вариант:
Проводимость наклонного канала в движущейся стенке зависит от направления течения газа:
1) p 1 > p 2.
2) P лев > P пр = f (α, u ст)
Предельное давление:

| (1.67) |
 |
где P 12– вероятность попадания молекулы газа в канал, падающей на стенку справа.
Струйная откачка

|
1.6.4. Физические методы откачки
1. Хемосорбция на пленках активных металлов (Ti, Zr, Ta и др.)
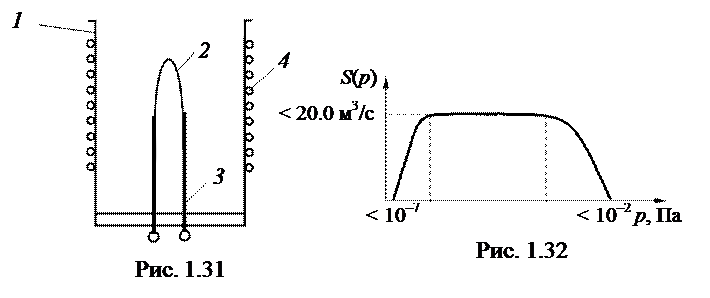
|
Теплота сорбции газов на титане в кДж/моль
| H2 | CO | N2 | O2 | CO2 | Ar | Kr | Xe |
| 19.3 | 8.38 | 16.8 | 35.5 |
2. Ионная откачка

|
3. Ионно-сорбционная откачка

|
4. Магниторазрядная откачка

|
5. Криогенная откачка
а) криоадсорбция: S 0 = 0.002–0.01 м3/с, p пр = 10–2– 1 Па
б) криоконденсация: S 0 = 0.025–4.1 м3/с, p пр = 10–10– 10–8 Па
Измерение давления
Измерение общего давления
Вакуумметр

|

|
Тепловой вакуумметр

|
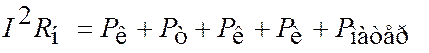
| (1.68) |

| (1.69) |

| (1.70) |

|

| (1.71) |

| (1.72) |
| Газ | N2 | O2 | Ar | H2O | H2 | He |
| qi | 1.06 | 1.06 | 1.08 | 0.63 | 0.274 | 0.57 |
Термопарный вакуумметр

|
