Центральное проецирование

Билет 1

 

ТОЧКА В ПРОСТРАНСТВЕ. ПОНЯТИЕ ОКТАНТОВ

Точка - неопределяемое понятие геометрии.
Положение точки А в пространстве необходимо и достаточно определяется тремя упорядоченными числами - ее координатами x_A, y_A, z_A в прямоугольной (декартовой) системе координат.
На комплексном чертеже точка необходимо и достаточно задается упорядоченной парой точек - двумя ее проекциями.
А' и А" лежат на одном перпендикуляре (линии связи) к оси x, при этом проекции точки могут быть построены по следующим значениям координат:
А' (x_A, y_A);
А" (x_A, z_A).

Точки общего положения - точки, у которых ни одна из координат не равна нулю:

точка A принадлежит I четверти пространства (+x_A, +y_A, +z_A);
точка В принадлежит II четверти пространства (+x_B, -y_B, +z_B);
точка C принадлежит III четверти пространства (+x_C, -y_C, -z_C);
точка D принадлежит IV четверти пространства (+x_D, +y_D, -z_D).

Точки частного положения - точки, у которых одна, две или три координаты равны нулю

Взаимно пересекаясь, плоскости Н, V и W делят пространство на восемь прямых трехгранных углов, называемых октантами (рис. 10). Римскими цифрами на чертеже показана нумера­ция октантов. При решении задач обычно пользуются первым октантом.

 

 

Положение точки в пространстве можно определить не толь­ко с помощью проекций, но и с помощью координат. Координа­тами называются числа, оп­ре­деляющие расстояние от точки до трех взаимно перпендикулярных плос­костей про­екций, кото­рые являются плоскостями координат. Линии взаимного пере­сече­ния плоскостей координат называются осями координат, а точка Опересе­чения осей – началом координат. Плоскости координат соответствуют плоскос­тям проекций. Оси коорди­нат соответствуют осям проекций и обозначаются оди­наково с ними.

Каждая точка пространства имеет три координаты: абсцис­су х, ординату у, аппликату z, как расстояния до плоскостей W, V и H соответственно. Коорди­на­ты откладывают вдоль осей, поэтому оси называют: о х – осью абсцисс, о у – осью ординат, о z – осью аппликат. Каждая проекция точки определяется двумя соответствующими координатами: горизонтальная – х и у, фронтальная – х и z, профильная – у и z

В зависимости от того, в каком октанте находится точка, ее координаты могут быть как положительными, так и отрица­тельными. В левой системе осей координат, обычно используе­мой в начертательной геометрии, направление оси о х влево от на­чала координат О считают положительным, а вправо – отрица­тельным. Направление оси о у от плоскости V (на наблюдателя) – положи­тель­ным, а за плоскость V – отрицательным. Направле­ние оси о z вверх – положи­тель­ным, вниз – отрицательным. При совмещении плоскостей координат сов­мещаются и оси, опреде­ляющие их.

Для построения чертежа точки по заданным координатам достаточно отложить от начала О значения координат (длины определенных отрезков) на соответствующих осях. Например, чтобы построить чертеж точки А с ко­орди­натами x =20, y =15, z=30, необходимо на осио х отложить отрезок О a _х==20 мм, на оси о у_н — отрезок Оа_Ун = 15мм, на оси о z — отрезок О а ₂=30 мм. Проведя затем линии проекционной связи, получают в их пере­сечении искомые проекции а, а' и а".

Билет 2

МЕТОД ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ ПЛОСКОСТЕЙ ДЛЯ ПОСТРОЕНИЯ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ПЛОСКОСТЯМИ

Этот метод применяется для построения линии пересечения двух поверхностей, когда секущие (параллельные) плоскости при пересе­чении с данными поверхностями образуют простые линии (прямую или окружность).

Задание: даны поверхности конуса и цилиндра ф (рис. 13.3). Требуется построить линию их пересечения.

Решение: ось цилиндра перпендикулярна к плоскости П₂, следо­вательно, поверхность цилиндра - проецирующая. В этом случае задача может быть решена так, как это было разобрано в предыдущем (п. 13.1.1) примере. Для этого определяют опорные - наивысшую и низшую точки 1 и 2, которые лежат на пересечении фронтальной про­екции цилиндра с очерковой образующей конуса. Их горизонтальные проекции 1₁и 2₁принадлежат горизонтальной проекции очерковой образующей конуса (l₁ и 2₁, совпадают с осевой линией конуса). Точ­ки 3 и 4 определяют видимость линий пересечения на горизонтальной проекции. Для определения их горизонтальных проекций через ось цилиндра параллельно П₁ проводят вспомогательную секущую плос­кость Г (ее фронтальный след Г₂). Эта плоскость рассечет цилиндр по очерковым образующим, а конус по окружности радиусомR, которая на П₁будет проецироваться в натуральную величину. Пересечение этой окружности с очерковыми образующими цилиндра есть не что иное, как горизонтальные проекции опорных точек 3₁к 4₁(рис. 13.3).

Построение промежуточных точек аналогично построению то­чек 3 и 4, только образующие, по которым вспомогательная плоскость будет рассекать цилиндр, не будут очерковыми (рис. 13.4).

 

Билет 3

МЕТОДЫПРОЕЦИРОВАНИЯ

Проецирование – процесс получения изображения предмета (пространственного объекта) на какой-либо поверхности с помощью световых или зрительных лучей (лучей, условно соединяющих глаз наблюдателя с какой-либо точкой пространственного объекта), которые называются проецирующими.

Центральное проецирование

Выбираем центр проецирования - произвольную точку S пространства и поверхность проецирования, не проходящую через точку S, например, плоскость проекций пи₀. Для того, чтобы спроецировать некоторую точку A пространства на плоскость p₀, необходимо через центр проецирования S провести проецирующую прямую SA до ее пересечения в точке A ₀ с плоскостью p₀.

При этом точка A ₀ называется проекцией точки A на плоскости пи₀. Проекцией фигуры называется совокупность проекций всех ее точек на выбранную поверхность проецирования (например, на рис. 1 проекцией треугольника BCD на плоскости p₀ является треугольник B ₀ C ₀ D ₀). Описанный метод проецирования путем проведения проецирующих прямых через точки заданной фигуры и центр проецирования, называется центральным.

S– центр или полюс проецирования

Пи_о - плоскость проекций

SA_о, SB₀, SC₀, SD₀ – проецирующие лучи (проецирующие прямые)

BCD – оригинал

Точки A₀, B₀, C₀, D₀ – центральные проекции точек A, B, C, D на плоскости пи

Кривая B₀C₀D₀ – центральная проекция кривой ABC

А_о - центральная проекция точки А на плоскость

Центральное проецирование – проецирование на заданную плоскость проекций из заданного полюса (центра) проецирования.

Основные свойства:

- любой геометрический элемент имеет на плоскости проекций единственную проекцию;

- любая точка на плоскости проекций является проекцией бесчисленного множества точек (любой точки, расположенной на проецирующем луче);

- проекцией прямой линии является прямая линия.

Достоинство – наглядность изображения.

Недостаток – сложность определения истинных размеров оригинала по его изображению.

2 Параллельное проецирование

Параллельное проецирование – проецирование с помощью параллельных проецирующих лучей; что наблюдется при бесконечном удалении полюса от плоскости проекций.

В случае, если проецирование осуществляется из бесконечно удаленной точки пространства, то все проецирующие прямые окажутся взаимно параллельными. Этот метод проецирования называется параллельным, а направление m, по которому оно осуществляется, - направлением (вектором) проецирования.

m – направление проецирования;

π₀ – горизонтальная плоскость проекций;

A, B, C, D – объекты проецирования – точки;

А ₀ и В₀, C₀, D₀ – проекции точек А и В на плоскость проекций π₀.

Основные свойства:

- любой геометрический элемент имеет на плоскости проекций единственную проекцию;

- любая точка на плоскости проекций является проекцией бесчисленного множества точек (любой точки, расположенной на проецирующем луче);

- проекцией прямой линии является прямая линия.

- проекции взаимно // прямых //, а отношение длин отрезков таких прямых равно отношению длин их проекций ;

- плоская фигура, // плоскости проекций проецируется на эту плоскость в натуральную величину;

- если прямая перпендикулярна направлению проецирования, то её проекцией является точка.

Параллельное проецирование разделяется на косоугольное прямоугольное.

Косоугольное – это проецирование с помощью лучей, наклоненных к плоскости проекций под некоторым отличным от прямого угла.

Прямоугольное (ортогональное) – это проецирование с помощью лучей, перпендикулярных к плоскости проекций.

Достоинство – легко определить размер.

Недостаток – меньшая наглядность.

3 Проецирование на плоскости координат. Метод Монжа

Метод изображения объектов по Монжу заключается в двух основных моментах:

1. Положение геометрического объекта в пространстве, в данном примере точки А, рассматривается относительно двух взаимно перпендикулярных плоскостей π₁ и π₂ (Рисунок 1.6).

Они условно разделяют пространство на четыре квадранта. Точка А расположена в первом квадранте. Декартова система координат послужила основой для проекций Монжа. Монж заменил понятие осей проекций на линию пересечения плоскостей проекций (координатные оси) и предложил совместить координатные плоскости в одну путем поворота их вокруг координатных осей.

Рисунок 1.6 – Модель построения проекций точки

π₁ – горизонтальная (первая) плоскость проекций

π₂ – фронтальная (вторая) плоскость проекций

π₁∩π₂ — ось проекций (обозначим π₂/π₁)

Рассмотрим пример проецирования точки А на две взаимно перпендикулярные плоскости проекций π₁ и π₂.

Опустим из точки А перпендикуляры (проецирующие лучи) на плоскости π₁ и π₂ и отметим их основания, то есть точки пересечения этих перпендикуляров (проецирующих лучей) с плоскостями проекций. А ₁ – горизонтальная (первая) проекция точки А;А ₂ – фронтальная (вторая) проекция точки А; АА ₁ и АА ₂ – проецирующие прямые. Стрелки показывают направление проецирования на плоскости проекций π₁ и π₂. Такая система позволяет однозначно определить положение точки относительно плоскостей проекций π₁ и π₂:

АА ₁⊥π₁

А ₂ А ₀⊥π₂/π₁ АА ₁ = А ₂ А ₀ — расстояние от точки А до плоскости π₁

АА ₂⊥π₂

А ₁ А ₀⊥π₂/π₁ АА ₂ = А₁А₀ — расстояние от точки А до плоскости π₂

2. Совместим поворотом вокруг оси проекций π₂/π₁ плоскости проекций в одну плоскость (π₁ с π₂), но так, чтобы изображения не накладывались друг на друга, (в направлении α, Рисунок 1.6), получим изображение, называемое прямоугольным чертежом (Рисунок 1.7):

Рисунок 1.7 – Ортогональный чертеж

Прямоугольный или ортогональный носит название эпюр Монжа.

Прямая А ₂ А ₁ называется линией проекционной связи, которая соединяет разноимённые проекции точки (А ₂ — фронтальную и А ₁ — горизонтальную) всегда перпендикулярна оси проекций (оси координат) А ₂ А ₁⊥π₂/π₁. На эпюре отрезки, обозначенные фигурными скобками, представляют собой:

· А ₀ А ₁ – расстояние от точки А до плоскости π₂, соответствующее координате y_А;

· А ₀ А ₂ – расстояние от точки А до плоскости π₁, соответствующее координате z_А.

 

Билет 4

ТОЧКА ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЙ В ОРТОГОНАЛЬНОЙ СИСТЕМЕ КООРДИНАТ

Точками общего положения, называют те точки, которые характеризуются тремя не нулевыми координатами.

Лежат в пространстве эпюра и их проекции не принадлежат осям эпюра.

Точки, принадлежащие элементам системы координат (плоскостям и осям), называются точками частного положения.

Первого рода.

- принадлежат плоскостям проекции (одна координата нулевая, та которая не содержится в содержащей их плоскости).

Второго рода.

- принадлежат осям координат (не нулевая только одна координата).

 

 

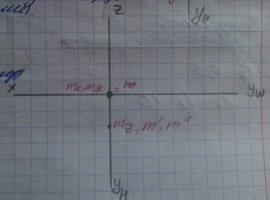
Билет 5

АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ. КООРДИНАТНЫЕ ОСИ. КОЭФФИЦИЕНТЫИСКАЖЕНИЯ ПО ОСЯМ

Аксонометрия – пространственное наглядное изображение.

Виды аксонометрии:

1. Косоугольная изометрия – наглядное изображение, получаемое путем косоугольного проецирования на плоскость, совмещенную с осями X и Z прямоугольную систему координат.

Направление, проецирующих лучей выбирают такое, чтобы проецируемая ось расположилась под 45 градусов к горизонту и уменьшилась в 2 раза.

2. Прямоугольная изометрия – изображение, полученное прямоугольным проецированием на плоскости одинаково наклонную к 3-ем осям системы координат.

3. Прямоугольная диметрия – прямоугольного проецирования на плоскость одинаково наклонного к 2-ум осям (X и Z), а наклон 3-ей оси выбирают, чтобы проецирование оси имели вид.

Коэффициент искажения – это отношение длины проекции отрезка оси на картинке к его истинной длине.

Декартова прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY, OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей. Ось OX называется осью абсцисс (или просто абсциссой), ось OY – осью ординат (ординатой), ось OZ – осью аппликат (аппликатой).

Векторы единичной длины, направленные вдоль координатных осей, называются координатными ортами. Их обозначают обычно как .

 

Билет 6

ОПРЕДЕЛЕНИЕ ИСТИНОЙ ДЛИНЫОТРЕЗКА ПРЯМОЙ МЕТОДОМ ТРАПЕЦИИ И ТРЕУГОЛЬНИКА

Если прямая занимает частное положение, то она проецируется без искажений на ту или те плоскости проекции, которым она параллельна.

Если прямая занимает общее положение, то истинную величину отрезка определяют, на эпюре построением базируясь на любой из его проекций.

Метод трапеции.

1. Выбираем любую из проекций и в ее конечных точках восстанавливаем к ней перпендикуляр.

2. На эти перпендикуляры откладываем недостающие координаты этой проекции, конечных точек отрезка (если знаки одинаковые, то в одну сторону, если нет, то в разные).

3. Соединяем концы перпендикуляров между собой, это и будет истинное значение.

Метод треугольника:

1) Из одного конца проекции восстанавливают перпендикуляр.

2) Откладывают на перпендикуляре алгебраическую разность недостающих координат для данной проекции.

3) Полученную точку соединяют с другим концом проекции. Полученный отрезок – истинная величина.

Метод вращения:

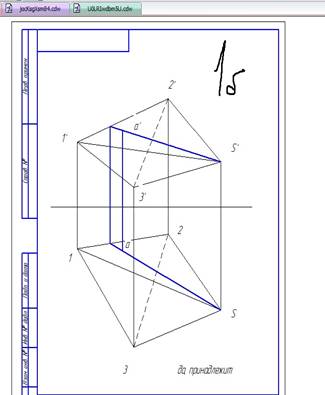
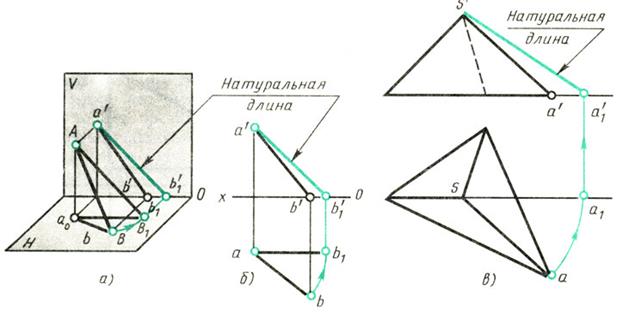
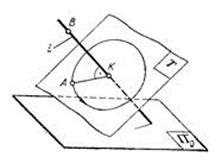
На рис. 173 показано, как определить способом вращения натуральную длину отрезка АВ прямой, наклонной к плоскостям проекций. На наглядном изображении (рис. 173, а) видно, что отрезок А В прямой не параллелен плоскостям проекций и, следовательно, проекции а'b' и ab отрезка изображаются искаженными. Нужно повернуть отрезок вокруг оси Аа, перпендикулярной к плоскости H, в направлении, указанном стрелкой, до положения, при котором отрезок станет параллельным плоскости V, т. е. в положение, обозначенное АВ₁. Тогда горизонтальная проекция аb отрезка АВ расположится параллельно плоскости V (параллельно оси х); обозначим ее аb₁. В этом положении проекция отрезка на плоскость V - линия а'b' представляет собой натуральную величину отрезка АВ.

Построение на чертеже начинают с горизонтальной проекции (рис. 173, б). Из точки а, как из центра, радиусом, равным ab, описывают дугу окружности bb₁ до пересечения с прямой, проведенной из точки а параллельно оси х. Получают новую горизонтальную проекцию b₁ точки В. Фронтальную проекцию b`<sub>1</sub> точки b<sub>1</sub>получают, восставив из нее перпендикуляр к оси х. Соединив прямой точку а' с точкой b` получают натуральную длину отрезка АВ.

На рис. 173, в показано, как можно данное построение применить к определению натуральной длины наклонного ребра треугольной пирамиды.

Метод перемены плоскостей проекций.

Этот способ отличается от способа вращения тем, что проецируемая линия или фигура остается неподвижной, а одну из плоскостей проекций заменяют новой дополнительной плоскостью, на которую и проецируют изображаемый элемент.

В пересечении новой плоскости Н₁ с плоскостью V (рис. 174, а) получают новую ось проекций х₁. Новую систему плоскостей на чертеже обозначают H₁/V

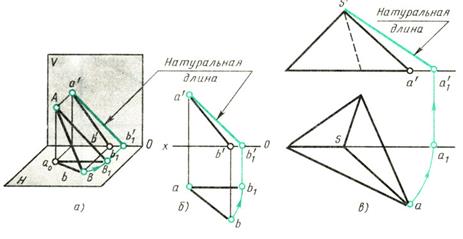
Дополнительную плоскость проекций Н₁ выбирают так, чтобы она была перпендикулярна фронтальной плоскости проекций V (рис. 174, а) и параллельна линии или плоскости фигуры, натуральную величину которой нужно определить. Линия или фигура спроецируется на дополнительную плоскость без искажений; новая ось проекций хх будет параллельна фронтальной проекции наклонной грани (рис. 174, б).

Рассматривая рис. 174, а и б, можно установить, что при перемене горизонтальной плоскости Н на новую Н₁ расстояние новой горизонтальной проекции любой точки до оси проекций х¹будет равно расстоянию прежней горизонтальной проекции этой точки до прежней оси проекций, т. е. расстояние точки А от плоскости V остается неизменным. Этим и пользуются при построении проекций фигур на дополнительную плоскость, которую затем совмещают с плоскостью чертежа.

На рис. 174, а точка А спроецирована сначала на плоскости V и H, т. е. получены ее проекции а' и а. Затем взята дополнительная плоскость H₁ перпендикулярная к плоскости V, и точка А спроецирована на дополнительную плоскость. Для этого из фронтальной проекции a` до точки А опущен перпендикуляр на плоскость H₁ пересечение которого с плоскостью дало точку ах₁. Затем от точки аx₁ отложено расстояние, равное аа_х, и получена искомая проекция a₁ точки А на дополнительную плоскость. Наклонная линия x₁ на чертеже обозначает новую ось проекций. Важно отметить, что фронтальная и новая проекции точки А лежат на одном перпендикуляре к оси х₁.

На рис. 174, б дано наглядное изображение четырехугольной призмы, верхняя грань которой наклонна. Чтобы определить натуральную величину верхней наклонной грани призмы, ее необходимо спроецировать на дополнительную плоскость. Построение проводят в следующем порядке. Вычерчивают фронтальную и горизонтальную проекции призмы. На произвольном расстоянии проводят новую ось проекции х₁ параллельно фронтальной проекции изображаемой грани. Из фронтальных проекций вершин наклонной грани - точек а`, b`, с`, d' восставляют перпендикуляры к новой оси x₁. На перпендикулярах от новой оси х₁ откладывают отрезки, равные расстояниям горизонтальных проекций этих точек от оси х. Соединив полученные точки а₁, b₁, с₁, d₁ прямыми линиями, получают натуральную величину грани.

Билет 7

МЕТОД КОНКУРИРУЮЩИХ ТОЧЕК. ОПРЕДЕЛЕНИЕ ВИДИМОСТИ ГЕОМЕТРИЧЕСКИХ ЭЛЕМЕНТОВ ОТНОСИТЕЛЬНО ДРУГ ОТ ДРУГА

Если проекции различных геометрических элементов накладываются друг на друга, то 1 проекция видима, а другая невидима.

Конкурирующими на данной плоскости координат точками называются точки, проекции которых на данной плоскости координат накладываются друг на друга.

Конкурирующими точками называются такие точки пространства, у которых совпадают их какие-либо две одноимённые проекции, на чертеже 57 показаны конкурирующие точки А и В (совпадают горизонтальные проекции А' = В') и С, В (совпадают фронтальные проекции С" = В").

Метод конкурирующих точек заключается в определении взаимной видимости точек по их несовпадающим проекциям. Так точка В находится выше точки А относительно π1 (Z_B > Z_A), поэтому на π1 видна точка В, которая закрывает точку А (считается, что наблюдатель смотрит на плоскость проекций из бесконечности и направление луча зрения параллельно проецирующему лучу S).

На π₂ видна точка D т.к. она находится ближе к наблюдателю (дальше от π₂, Y_D > Y_C) и закрывает невидимую точку С.

Пользуясь этим методом (черт. 58), можно определить, что пря­мая а проходит над прямой b, т.к. точка А, принадлежащая этой прямой а, расположена выше точки В, находящейся на прямой b (Z_A>Z_B).

Изобразим прямоугольные проекции двух скрещивающихся прямых AB и CD. В точку пересечениях их горизонтальных проекций проецируются две точки: Точка 1, принадлежащая прямой АВ и точка 2, принадлежащая прямой CD. Эти точки называются конкурирующими. С их помощью определяется взаимное положение прямых относительно плоскостей проекции (видимость проекций геометрических элементов).

Так, в нашем случае, приведенном рисунке, луч, проецирующий прямые на плоскость пи1, встретит раньше точку 1. Следовательно, эта часть прямой AB расположена выше прямой CD. Аналогично определим, что левая часть прямой AB расположена дальше от плоскости пи2 вместе с принадлежащей ей точкой 3, чем прямая CD. В общем случае при определении видимости прямоугольных проекций на плоскости пи1 направление проецирующего луча принимают заданным сверху вниз, на плоскости пи2 - снизу вверх и на плоскости пи3 - слева направо.

 

Билет 8

СПОСОБЫПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ. МЕТОД ПЕРЕМЕНЫПЛОСКОСТЕЙ

Метод вращения:

Сущность метода заключается в том, что заданный геометрический элемент вращением вокруг некоторой неподвижной прямой (оси вращения) приводят в положение, удобное для решения поставленной задачи.

- при вращении точки вокруг оси, перпендикулярной к плоскости пи 1, ее горизонтальная проекции перемещается по окружности, а фронтальная проекция по прямой, параллельной оси ОХ.

- при вращении точки вокруг оси, перпендикулярной к плоскости пи2, фронтальная проекция точки будет перемещаться по дуге окружности, а ее горизонтальная проекция – по прямой, параллельной оси ОХ.

- при вращении отрезка прямой округ оси, перпендикулярной к плоскости пи1, горизонтальная проекция его не изменяет длины.

- при определении истинной длины отрезка методом вращения одновременно определяется угол наклона этого отрезка к одной из плоскостей координат.

- для того, чтобы повернуть плоскость вокруг некоторой оси, достаточно повернуть вокруг нее геометрические элементы, определяющие ее положение.

Положения для решения задачи:

1. точка А при вращении вокруг некоторой оси i перемещается в плоскости Т, которую условимся называть плоскостью вращения и которая расположена перпендикулярно к этой оси;

2. траекторией движения точки является окружность, центр которой определяется как точка К. пересечения плоскости Т с осью вращения;

3. радиус АК окружности перпендикулярен к оси вращения. При вращении точки В (рис. 4.2) вокруг вертикальной оси точка описывает в горизонтальной плоскости Г окружность радиуса ВК, которая на плоскость проекций По проецируется без искажения. Если точку В повернуть вокруг оси i на угол b, то и проекция точки на плане переместится по дуге окружности на такой же угол и займет положение B₂. На рис. 4.3 рассматривается случай вращения точки А вокруг вертикальной оси i до совмещения ее с плоскостью S. Точка A будет принадлежать плоскости S при условии, если она при вращении окажется расположенной на горизонтальной плоскости с той же числовой отметкой, что и у точки А.

Строим линию пересечения плоскости вращения Г с плоскостью Σ - h_5,5 проводим из центра вращения точки К_5,5 дугу окружности радиуса К_5,5А_5,5. До пересечения с горизонталью h_{5,5 .} Таким образом, точка А после поворота займет положение А_5,5 и А_5,5.

Метод вращения позволяет сделать плоскость общего положения, параллельной плоскости координат:

1. Последовательное вращение плоскости вокруг осей, перпендикулярных к плоскостям проекций;

2. Вращение плоскости вокруг горизонтали или фронтали.

На рис. 173 показано, как определить способом вращения натуральную длину отрезка АВ прямой, наклонной к плоскостям проекций. На наглядном изображении (рис. 173, а) видно, что отрезок А В прямой не параллелен плоскостям проекций и, следовательно, проекции а'b' и ab отрезка изображаются искаженными. Нужно повернуть отрезок вокруг оси Аа, перпендикулярной к плоскости H, в направлении, указанном стрелкой, до положения, при котором отрезок станет параллельным плоскости V, т. е. в положение, обозначенное АВ₁. Тогда горизонтальная проекция аb отрезка АВ расположится параллельно плоскости V (параллельно оси х); обозначим ее аb₁. В этом положении проекция отрезка на плоскость V - линия а'b' представляет собой натуральную величину отрезка АВ.

Построение на чертеже начинают с горизонтальной проекции (рис. 173, б). Из точки а, как из центра, радиусом, равным ab, описывают дугу окружности bb₁ до пересечения с прямой, проведенной из точки а параллельно оси х. Получают новую горизонтальную проекцию b₁ точки В. Фронтальную проекцию b`<sub>1</sub> точки b<sub>1</sub>получают, восставив из нее перпендикуляр к оси х. Соединив прямой точку а' с точкой b` получают натуральную длину отрезка АВ.

На рис. 173, в показано, как можно данное построение применить к определению натуральной длины наклонного ребра треугольной пирамиды.

Метод перемены плоскостей проекций.

Сущность метода заключается в том, что заданный геометрический элемент проецируют на новую плоскость проекций, обычно перпендикулярную к одной из старых плоскостей проекций. Новая плоскость проекций выбирается так, чтобы рассматриваемый элемент проецировался на нее наиболее удобно для решения поставленной задачи.

- при перемене плоскости пи2 на новую фронтальную плоскость проекций, перпендикулярную плоскости пи1, координат z проецируемой точки остается неизменной.

- при перемене плоскости пи1 на новую горизонтальную плоскость проекций, перпендикулярную к плоскости пи2, остается неизменной координата y проецируемой точки.

- если концы заданного отрезка имеют координаты разные по знаку, то значения этих координат откладываются в противоположные стороны по отношению у новой оси проекции.

Перемена одной плоскости проекций. Даны проекции точки A (A₁ А₂) (фиг.257,а).
Заменим плоскость П₃ новой плоскостью П₄, перпендикулярной к плоскостиП₄ получим новую систему П₃, П₄ двух взаимно перпендикулярных плоскостей с новой осью s₁₄.

Спроектируем точку А на новую плоскость П₄, получим новую проекцию A₄точки А. Рассматривая изображение на (фиг.257,а), замечаем, что расстояние от новой проекции A₄ до новой оси s₁₄ равно расстоянию от старой проекции A₂ до старой оси х₁₂ (A₄A₁₄ = А₂A₁₂), т.е. отрезок z_A4 = z_A2
Порядок построения новой проекции на комплексном чертеже сводится к следующему: проводят новую ось s₁₄ и обозначают новую систему плоскостей проекций П₁, П₄, затем из проекции А₁ проводят линию связи перпендикулярно новой оси проекций s₁₄ и на продолжении этой линии связи от точки A₁₄ откладывают расстояние, равное расстоянию от старой проекции точки до старой оси проекции, т. е. А₂А₁₂ или z_A2.
Получим проекцию A₄ данной точки А на новой плоскости проекций П₄. Аналогично выполняют построение при замене плоскости П₁ новой плоскостью. На (фиг.257,б) плоскость П₁ заменена плоскостью П₅.
Наносят новую ось s₂₅. Проводят линию связи перпендикулярно новой осиs₂₅ и на ней от точки А₂₅ откладывают расстояние У_А1 = У_А5 получают точку А₅ - новую проекцию точки А.
Как видно из приведенных примеров, выбранная новая плоскость проекций должна быть перпендикулярна оставшимся, причем плоскости должны заменяться последовательно. Скачала, например, заменить плоскость П₁, а затем плоскость П₂, и так можно повторять столько раз, сколько это потребуется.

Этот способ отличается от способа вращения тем, что проецируемая линия или фигура остается неподвижной, а одну из плоскостей проекций заменяют новой дополнительной плоскостью, на которую и проецируют изображаемый элемент.

В пересечении новой плоскости Н₁ с плоскостью V (рис. 174, а) получают новую ось проекций х₁. Новую систему плоскостей на чертеже обозначают H₁/V

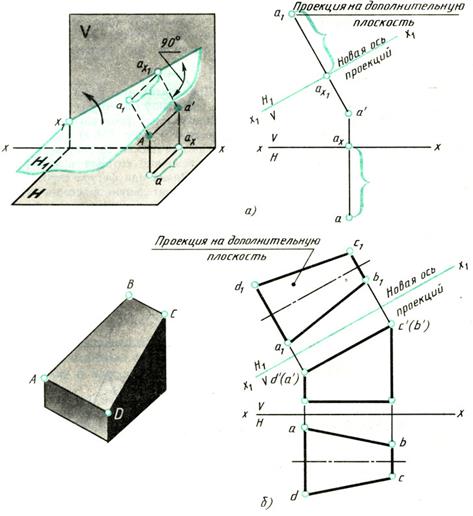
Дополнительную плоскость проекций Н₁ выбирают так, чтобы она была перпендикулярна фронтальной плоскости проекций V (рис. 174, а) и параллельна линии или плоскости фигуры, натуральную величину которой нужно определить. Линия или фигура спроецируется на дополнительную плоскость без искажений; новая ось проекций хх будет параллельна фронтальной проекции наклонной грани (рис. 174, б).

Рассматривая рис. 174, а и б, можно установить, что при перемене горизонтальной плоскости Н на новую Н₁ расстояние новой горизонтальной проекции любой точки до оси проекций х¹будет равно расстоянию прежней горизонтальной проекции этой точки до прежней оси проекций, т. е. расстояние точки А от плоскости V остается неизменным. Этим и пользуются при построении проекций фигур на дополнительную плоскость, которую затем совмещают с плоскостью чертежа.

На рис. 174, а точка А спроецирована сначала на плоскости V и H, т. е. получены ее проекции а' и а. Затем взята дополнительная плоскость H₁ перпендикулярная к плоскости V, и точка А спроецирована на дополнительную плоскость. Для этого из фронтальной проекции a` до точки А опущен перпендикуляр на плоскость H₁ пересечение которого с плоскостью дало точку ах₁. Затем от точки аx₁ отложено расстояние, равное аа_х, и получена искомая проекция a₁ точки А на дополнительную плоскость. Наклонная линия x₁ на чертеже обозначает новую ось проекций. Важно отметить, что фронтальная и новая проекции точки А лежат на одном перпендикуляре к оси х₁.

На рис. 174, б дано наглядное изображение четырехугольной призмы, верхняя грань которой наклонна. Чтобы определить натуральную величину верхней наклонной грани призмы, ее необходимо спроецировать на дополнительную плоскость. Построение проводят в следующем порядке. Вычерчивают фронтальную и горизонтальную проекции призмы. На произвольном расстоянии проводят новую ось проекции х₁ параллельно фронтальной проекции изображаемой грани. Из фронтальных проекций вершин наклонной грани - точек а`, b`, с`, d' восставляют перпендикуляры к новой оси x₁. На перпендикулярах от новой оси х₁ откладывают отрезки, равные расстояниям горизонтальных проекций этих точек от оси х. Соединив полученные точки а₁, b₁, с₁, d₁ прямыми линиями, получают натуральную величину грани.

 

 

 

Билет 9

СПОСОБЫОПРЕДЕЛЕНИЯ ТОЧКИ ВСТРЕЧИ ПРЯМОЙ С ПЛОСКОСТЬЮ. АЛГОРИТМ РЕШЕНИЯ

Точку пересечения (встречи) прямой линии с плоскостью определяют тремя последовательными построениями:

1) Заданную прямую заключают в вспомогательную плоскость, обычно проецирующую, т.к. для проецирующей плоскости не надо находить следов заданной прямой.
(1 след проецирующей плоскости совпадает с соответствующей проекцией заданной прямой, а др. след параллелен соответствующей оси координат).

2) Находят линию пересечения вспомогательной плоскости с заданной плоскостью.

3) Отмечают точку пересечения заданной прямой с найденной линией пересечения.

4) Определяют видимость прямой линии.

Случай 1.

Прямая общего положения пересекает плоскость общего положения.