Однофазные цепи переменного тока.

Электрические цепи однофазного синусоидального тока

Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону

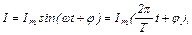
где – амплитуда тока;

- начальная фаза;

– период колебания;

- угловая частота

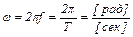Любая синусоидальная функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.

Рисунок 1. Зависимость тока от частоты.

Среднее и действующее значение синусоидально изменяющейся величины.

Под средним значением синусоидально изменяющейся величины понимают среднее значение этой величины за половину периода. Так среднее значение тока

т.е. .

В электротехнике широко применяется понятие действующего значения синусоидально изменяющейся величины (его также называют эффективным или среднеквадратичным). Действующее значение тока:

Действующее значение тока равно от амплитуды.

Аналогично

Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока , текущего по тому же сопротивлению.

Количество теплоты, выделенное за один период синусоидальным током:

Выделенная за то же время постоянным током теплота будет равна

Приравняем их:

тогда

Таким образом, действующее значение синусоидального тока численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.

Приборы электромагнитной, электродинамической и тепловой систем показывают действующее значение измеряемой величины.

Изображение синусоидально изменяющихся величин векторами на комплексной плоскости.

(формула Эйлера).

Комплексное число изображают на комплексной плоскости вектором, численно равным единице и составляющим угол 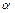с осью вещественных значений (ось ). Угол 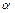отсчитывается против часовой стрелки от оси .

Модуль функции равен единице:

Если вместо функции взять функцию , то

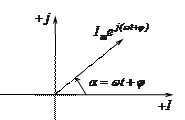
Рисунок 2.

Положим, что , тогда

- действительная часть комплексного числа.

С целью единообразия принято на комплексной плоскости изображать векторы синусоидально изменяющихся величин для момента времени . При этом

где 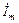- комплексная амплитуда, ,

- угол, под которым вектор проведен к оси .

Под комплексом действующего значения тока или под комплексом тока понимают частное от деления комплексной амплитуды на

Цепь с активным сопротивлением.

Ток в цепи можно определить, пользуясь законом Ома для мгновенных значений

Мгновенная мощность в цепи:

Среднее значение мощности за период

Цепь с индуктивностью.

Индуктивность в цепи с изменяющимся током характеризует наличие изменяющегося магнитного поля, созданного этим током. В электрических цепях постоянного тока созданное магнитное поле неизменно и не оказывает влияния на режим работы цепи. В цепях переменного тока всякое изменение тока вызывает изменение магнитного потока, т.е. изменение его собственного потокосцепления. Вследствие этого в отдельных элементах цепи наводится ЭДС.

Наведение ЭДС в элементе цепи при изменении его собственного потокосцепления называется явлением самоиндукции. ЭДС самоиндукции определится

Потокосцепление . зависит от тока , протекающего в цепи, тогда

Когда поле образуется в среде с постоянной проницаемостью, зависимость от является линейной, тогда

- индуктивность катушки.

Пусть в катушке с индуктивностью 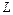протекает синусоидальный ток.

Положительное направление ЭДС самоиндукции совпадает с положительным направлением тока:

По второму закону Кирхгофа:

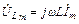- комплексное сопротивление индуктивности.

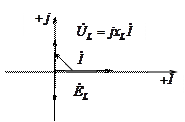
Величину называют индуктивным сопротивлением.

Тогда закон Ома в комплексной форме для цепи с индуктивностью можно представить:

В цепи с индуктивностью происходит непрерывный обмен энергией между цепью и магнитным полем без затрат энергии от источника.

Амплитуду колебаний мощности в цепи с индуктивностью называют реактивной индуктивной мощностью и обозначают :

[Вар].

Цепь с емкостью.

- реактивное сопротивление емкости или емкостное сопротивление.

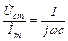- комплексное сопротивление емкости.

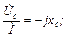
- закон Ома в комплексной форме.

- реактивная емкостная мощность.

Цепь, содержащая катушку с активным сопротивлением и индуктивностью.

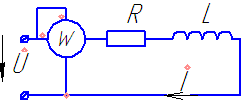
Согласно второму закону Кирхгофа:

Комплексное число имеет размерность сопротивления и является коэффициентом пропорциональности между комплексными значениями напряжения и тока. Величину называют комплексным полным сопротивлением цепи:

- модуль комплексного полного сопротивления цепи,

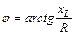- угол сдвига между током и напряжением на зажимах цепи.

Если каждую из сторон треугольника напряжений разделить на ток, то получим треугольник сопротивлений. Из этого треугольника можно определить угол сдвига фаз:

Векторная диаграмма катушки с активным сопротивлением

Расчет цепи можно вести 2 путями:

Расчет по модулям тока и напряжения. Для этого сначала определяют модуль полного сопротивления цепи и угол сдвига фаз . Затем, в зависимости от условий задачи, находят действующие значения напряжения или тока. После этого записывают мгновенное значение напряжения или тока с учетом начальной фазы и угла сдвига фаз.
Расчет ведут комплексным методом. При этом пользуются законами Ома и Кирхгофа в комплексной форме записи. Напряжения, токи, сопротивления записывают в комплексной форме и проводят расчет для комплексных величин.

Мощность в цепи, состоящей из последовательно соединенных активного сопротивления и индуктивности.

Пусть ток в цепи

тогда напряжение на зажимах цепи

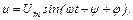
где - начальная фаза,

- угол сдвига фаз между и .

Мгновенное значение мощности:

;

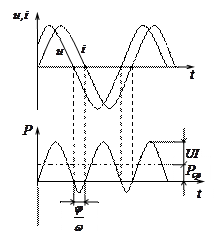
Так как то

Видно, что средняя мощность равна активной мощности. Активная мощность равна произведению действующих значений тока и напряжения, умноженному на косинус сдвига фаз между током и напряжением.

Наибольшее значение активной мощности, которое может быть получено при значениях тока и напряжения в цепи называют полной мощностью

Мощность, запасаемая в реактивном элементе, называется реактивной мощностью

Запишем:

Тогда .

Мощности имеют одну и ту же размерность, но для их измерения введены единицы различных наименований

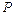[Вт];

[Вар] – вольт-ампер реактивный;

[В×A] – вольт-ампер.

Аналогично треугольнику сопротивлений можно представить треугольник мощностей:

Полная мощность характеризует амплитуду колебаний мощности в цепи. Кроме того полная мощность учитывает напряжение и ток.

Активная мощность 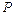является средней мощностью преобразования электрической энергии в другие виды энергии. Её величина зависит не только от тока и напряжения в цепи, но и от , который называют коэффициентом мощности

Активную, реактивную и полную мощности можно получить через комплексные действующие значения напряжения и тока . Для этого необходимо взять сопряженный комплексный ток и умножить на комплексное напряжение:

где .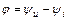

Произведение называют комплексной полной мощностью.

Действительной частью комплексной полной мощности является активная мощность 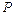, а мнимой частью комплексной мощности – реактивная. Если мнимая часть положительна, то реактивная мощность носит индуктивный характер, если отрицательная, то емкостный.

Измерение активной мощности.

Последовательное соединение катушки и конденсатора в цепи синусоидального тока.

Резонанс напряжений.

Полное комплексное сопротивление цепи:

В зависимости от соотношения между и 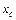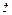может носить индуктивный характер, емкостный или быть чисто активным:

1. - цепь носит индуктивный характер:

2. - цепь носит емкостный характер:

3. - цепь носит активный характер:

Запишем комплексное сопротивление в показательной форме:

Положительное значение означает, что реактивное сопротивление имеет индуктивный характер. При 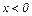цепь носит емкостный характер.

Явление при последовательном соединении элементов 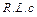, когда общее напряжение цепи совпадает по фазе с током в цепи, называют резонансом напряжений.

Условие резонанса:

При резонансе емкостные и индуктивные напряжения компенсируют друг друга. , так как они равны по величине и противоположны по знаку. Отношение или к при резонансе называется добротностью цепи или добротностью контура.

При 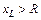, поэтому напряжение на конденсаторе или индуктивности превышает при резонансе входное напряжение.

Рассмотрим полную комплексную мощность рассматриваемой цепи.

где - реактивная мощность, обусловленная наличием в цепи индуктивности;

- реактивная мощность, обусловленная наличием в цепи емкости.

Цепь с параллельно соединенными приемниками.

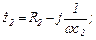
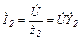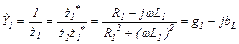Из приведенного уравнения видно, что ток в цепи будет определяться величинами . В схеме, образованной двумя параллельными ветвями с разнохарактерными реактивными сопротивлениями возможны резонансные явления. По определению резонансного режима ток должен совпадать по фазе с напряжением .

Из уравнения видно, что это происходит, когда:

, или .

Видно, что резонансная частота определяется параметрами .

Определим полную комплексную мощность в цепи

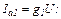
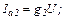
Тогда:

Повышение коэффициента мощности

в цепях синусоидального тока.

Большинство современных потребителей электрической энергии представляют собой индуктивные нагрузки, токи которых отстают по фазе от напряжений питающего источника. Активная мощность таких потребителей при заданных значениях тока и напряжения зависит от cosj.

Для потребителя задается его U и активная мощность P. С уменьшением cosj потребителя ток его возрастает:

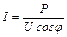Генераторы рассчитываются на определенную номинальную мощность . При заданном напряжении 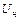, ток не должен превышать . Чтобы ток генератора не превышал номинального значения при снижении потребителя необходимо снижать его активную мощность. В этом случае генератор будет нагружен по току, но недогружен по активной мощности.

Для сохранения неизменной активной мощности при снижении необходим генератор большей номинальной мощности.

Недогрузка генератора активной мощностью снижает КПД всей установки. Себестоимость энергии от этого повышается.

Работа потребителя с малым приводит к увеличению потерь энергии в проводах и на внутреннем сопротивлении генератора.

Если сопротивление внутренней энергии цепи , то мощность потерь:

При уменьшении мощность потерь возрастает.

Методы повышения .

В номинальном режиме потребители имеют довольно высокий . Необходимо, чтобы потребитель всегда работал в номинальном режиме.
Снизить ток потребителя можно за счет уменьшения реактивного тока индуктивного потребителя.

Обычно рассчитывают емкость, чтобы .

Расчет сложной цепи синусоидального тока.

Можно пользоваться любым из методов расчета (контурных токов, узловых потенциалов, экв. генер.).

Нужно только все величины представить в комплексной форме.

Цепи синусоидального тока с взаимноиндуктивной связью.

На схемах с взаимной индукцией направление намотки витков не указывают, но помечают одноименные зажимы точками. Одноименными называются такие зажимы, по отношению к которым одинаково ориентированные токи создают одинаково положительно направленные потоки самоиндукции и взаимной индукции.

Из рассмотренных схем видно, что ЭДС взаимной индукции и наводящие их токи направлены от одноименных зажимов катушек.

Составим уравнения по второму закону Кирхгофа (2 схема)

Уравнения электрического состояния контуров:

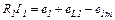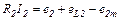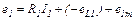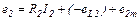Условимся, что положительные направления напряжений взаимной индукции и ЭДС взаимной индукции совпадают. Тогда можно записать:

, ,

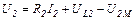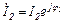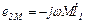Тогда:

Знак «+» берётся при согласном включении, «-» при встречном.

Воздушный трансформатор.

Если к зажимам второй катушки подключить нагрузку с сопротивлением , то получившаяся цепь образует воздушный трансформатор. При помощи трансформатора энергия первичного напряжения преобразуется в энергию вторичного напряжения .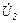

Вторичная обмотка трансформатора является генераторной обмоткой, ЭДС которой . ЭДС будет ориентирована относительно одноименного зажима катушки аналогично ориентации тока . На рисунке направлена от зажима, помеченного точкой, аналогично направлению тока . Условно положительное направление тока совпадает с положительным направлением , как во всякой генераторной обмотке. 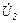принято считать совпадающим с направлением нагрузки.

Получившаяся система представляет собой согласное включение, поэтому можно записать уравнение:

Перепишем уравнения:

(1) ,

(2) ,

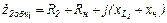Представим трансформатор эквивалентным двухполюсником. Выразим из уравнения (2) :

, подставим в (1):

- вносимое сопротивление.

Величину называют передаточным числом. Вносимое сопротивление характеризует влияние вторичной цепи на первичную. Величину можно представить в виде вносимого активного и реактивного сопротивлений.

Тогда .

Комплексное полное вносимое сопротивление имеет отрицательную мнимую часть. Следовательно, индуктивное сопротивление вторичной цепи переносится в эквивалентную схему в виде емкости.

Эквивалентная схема трансформатора может быть представлена:

Расчет сложной цепи с магнитной связью.

Для расчета цепи составим уравнение по третьему закону Кирхгофа, предварительно указав направления токов в ветвях. Чтобы учесть направление ЭДС взаимной индукции, необходимо помнить, что их направления зависят только от направлений наводящих их токов. Ток первый проходит от зажима намеченного точкой, следовательно, ЭДС, наводимые этим током во второй катушке и третьей, направлены от тех же (одноименных) зажимов. С ЭДС совпадают по направлению и напряжения.

Трехфазные электрические цепи.

Многофазными цепями называются цепи, в которых действуют синусоидальные ЭДС одинаковой частоты, отличающиеся по фазе одна от другой и создаваемые одним источником энергии. Каждую из цепей, входящих в многофазную цепь, называют фазой. Многофазными цепями называются цепи, в которых действуют синусоидальные ЭДС одинаковой частоты, отличающиеся по фазе одна от другой и создаваемые одним источником энергии. Цепи, в зависимости от числа фаз называют двухфазными, трехфазными, шестифазными и т.д. Наибольшее распространение получили трехфазные цепи. Их преимущества: экономичность передачи энергии по сравнению с однофазными цепями, возможность получения кругового вращающегося поля, необходимого для трехфазного асинхронного двигателя, возможность получения двух напряжения – фазного и линейного.

Рассмотрим принцип действия трехфазного генератора

Витки сдвинуты относительно друг друга на угол . ЭДС в неподвижных витках обмотки статора наводятся в результате пересечения их магнитным полем вращающегося ротора. Поле ротора возбуждается обмоткой, питаемой постоянным током. Или ротор состоит из постоянных магнитов. При вращении ротора с равномерной скоростью в обмотках фаз статора возникают периодически изменяющиеся ЭДС одинаковой частоты, но отличающиеся друг от друга по фазе вследствие их пространственного смещения.

Если наведенные ЭДС имеют одинаковые амплитуды и сдвинуты по фазе относительно друг друга на , то такая система ЭДС называется симметричной.

Если принять начальную фазу ЭДС обмотки А за нулевую, то можно записать:

, ,

, .

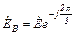За положительное направление ЭДС принимаем направление от конца к началу каждой фазы.

Система ЭДС в которой ЭДС фазы B отстает по фазе от ЭДС фазы A, а ЭДС фазы C отстает от ЭДС фазы B называют ЭДС прямой последовательности. Если изменить направление вращения ротора, то последовательность чередования фаз изменится и будет называться обратной.

Последовательность фаз определяет направление вращения трехфазных двигателей.

Если фазы обмотки статора электрически не соединены между собой, то они образуют несвязанную трехфазную цепь. В этом случае каждая из фаз соединена с двумя проводами с приемником.

Несвязанные цепи не получили широкого распространения вследствие их низкой экономичности, вызванной большим числом проводов, соединяющих генератор и приемник.

Более совершенными являются связанные цепи, в которых фазы обмоток электрически соединены между собой. Различают соединение фаз генератора и приемника в звезду и в треугольник

Соединение в звезду.

Концы фаз генератора XYZ соединяют в одну общую точку, называемую нейтралью. Общая точка соединения концов фаз приемника – нейтральная точка приемника. Провода, соединяющие начала фаз обмоток генератора и приемника называют линейными проводами. Провод, соединяющий нейтральные точки генератора и приемника называют нейтральным.

Напряжения между началом и концом каждой фазы генератора называют фазными, а напряжения между началами фаз - линейными.

По аналогии с фазными и линейными напряжениями различают фазные и линейные токи. Фазные – токи в фазах генератора и приемниках, линейные – токи в линейных проводах.

При соединении звездой фазные и линейные токи одинаковы:

При измерении линейных напряжений вольтметрами принято считать условно положительное направление тока в вольтметрах по часовой стрелке.

В этом случае вольтметры измеряют напряжения , , . Эти напряжения могут быть определены из уравнений, составленных по второму закону Кирхгофа:

В соответствии с этими уравнениями построена топографическая диаграмма:

Из диаграммы . Расчет токов в фазах нагрузки и в нейтральном проводе может быть проведен:

; ; ,

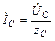Угол сдвига фаз тока и напряжения определяется характером нагрузки. Нагрузка называется симметричной, если комплексные сопротивления фаз равны между собой.

Если это условие не выполняется, то нагрузка будет несимметричной. При этом нагрузка будет равномерной, если или однородной, если .

Сопротивление нейтрального провода обычно значительно меньше сопротивления фаз приемника, поэтому падением напряжения на нейтральном проводе пренебрегают и считают фазные напряжения приемника симметричными и равными по фазе и по величине напряжениям генератора.

При несимметричной нагрузке токи в фазах будут различны, но благодаря нейтронному проводу напряжение на каждой фазе при изменении нагрузки практически остается неизменным и равным фазному напряжению генератора.

Если сопротивлением нейтрального провода не пренебрегать, то при напряжения на фазах нагрузки не будут равны напряжениям генератора.