Задание: изучить материал урока, записать таблицу первообразных (можно без производных) и правила нахождения первообразных, выполнить самостоятельную работу и домашнее задание.
Урок-лекция
Тема: «Первообразная и интеграл»
Цели урока.
Познакомиться с определением первообразной, формулами и правилами её нахождения, с интегралом и его свойствами.
Лекция
1. Материальная точка движется со скоростью 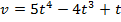
Найдите закон изменения пути от времени. Нужна операция, обратная дифференцированию.
Необходимо найти функцию по производной. Такая функция называется первообразной, а операция, обратная дифференцированию носит название операции интегрирования.
Определение. Функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для всех x из этого промежутка выполняется равенство F '(x) = f(x).
2. Будет ли функция 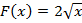 первообразной для
первообразной для 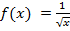 на интервале
на интервале 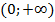 ?
?
Решение. 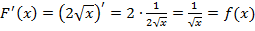 для всех
для всех 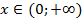 .
.
Ответ: 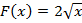 является первообразной для
является первообразной для 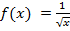 на интервале
на интервале 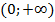 .
.
Первообразная данной функции определена не однозначно, и ее нахождение имеет бесконечно много решений. Если к функции 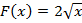 прибавим постоянную величину С, то
прибавим постоянную величину С, то 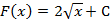 также является первообразной для функции
также является первообразной для функции 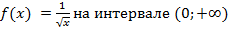 , т. к. при проверке
, т. к. при проверке 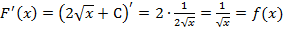 .
.
Теорема. Если F(x) – первообразная для функции f(x) на промежутке J, то F(x) + C, где C – 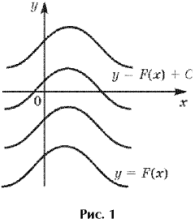 постоянная, также является первообразной для f(x) на J.
постоянная, также является первообразной для f(x) на J.
Это основное свойство первообразных.
Геометрический смысл основного свойства первообразной. Графики всех первообразных функции f(x) получаются из любого из них параллельным переносом вдоль оси Oy
Для нахождения первообразной будем пользоваться формулами:
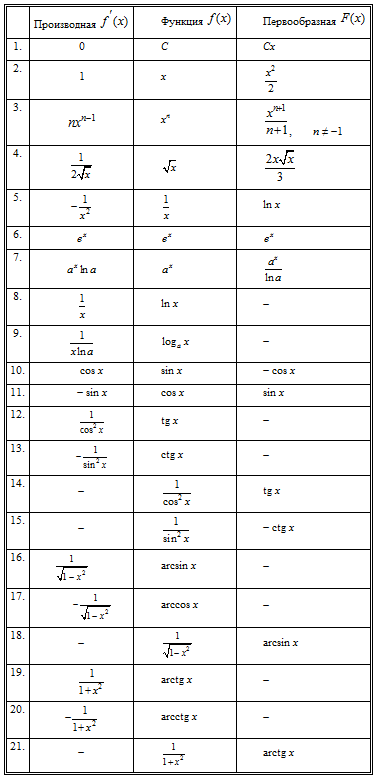

В данной таблице присутствуют формулы производных, не ошибитесь при использовании таблицы.
Пример:
Для функции f(x) = x2 найдите первообразную, график которой проходит через точку (3; 7).
Решение. Первообразная для f(x) = x2 найдём по формуле 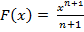 , получим
, получим 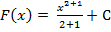 или
или
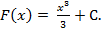 Подставим в полученное равенство координаты точки (3;7):
Подставим в полученное равенство координаты точки (3;7): 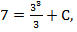 7= 9 + C, C = – 2. Получаем первообразную:
7= 9 + C, C = – 2. Получаем первообразную: 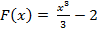 или
или 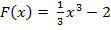
Ответ: 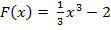
Для нахождения первообразных запомним три правила:
Правило 1. Если F есть первообразная ƒ, а G- первообразная для g, то F+G есть первообразная для ƒ+g (первообразная двух функций равна сумме их первообразных).
Правило 2. Если F есть первообразная для функции ƒ, а k-постоянная, то kF есть первообразная для функции kƒ.
Правило 3. Если F(x) есть первообразная для функции ƒ(x), а k и b - постоянные, причем k 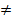 0, то
0, то 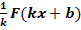 есть первообразная для функции ƒ(kx+b).
есть первообразная для функции ƒ(kx+b).
Теперь мы можем вернуться к началу урока и решить задачу: Материальная точка движется со скоростью 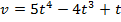 . Найдите закон изменения пути от времени.
. Найдите закон изменения пути от времени.
Закон изменения пути от времени 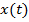 является первообразной для функции скорости
является первообразной для функции скорости 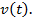
Найдём первообразную скорости 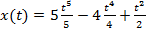 =
= 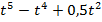 ,
, 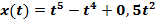
Пример: Найдите все первообразные для функций: 1) 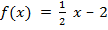 ; 2) f(x) = 2cosx;
; 2) f(x) = 2cosx;
3) f(x) = 8 – 5x + 10х2; 4) f(x) = (4 – 3х)9; 5) f(x) = -4sin3x
Решения:
1) 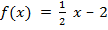 ,
, 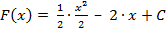 ,
, 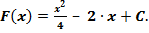
2) 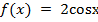 ,
, 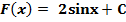 .
.
3) 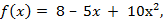
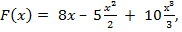
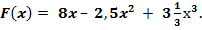
4) f(x) = (4 – 3х)9 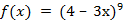 , Fx=-13∙4 – 3х1010 + C
, Fx=-13∙4 – 3х1010 + C 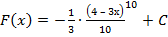 , Fx=-130∙4 – 3х10+C.
, Fx=-130∙4 – 3х10+C. 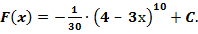
5) f(x) = -4sin3x 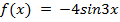 , Fx= -4∙-13cos3x+C,
, Fx= -4∙-13cos3x+C, 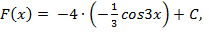 Fx=43cos3x +C
Fx=43cos3x +C 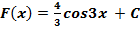 .
.
1. Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 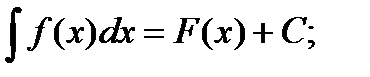
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1) 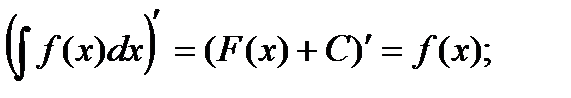
2) 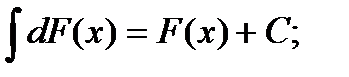
3) 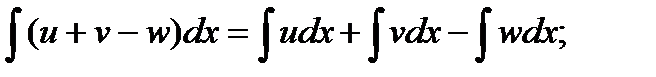 где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.
4) 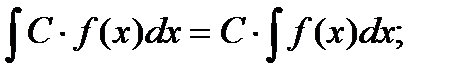
Пример: 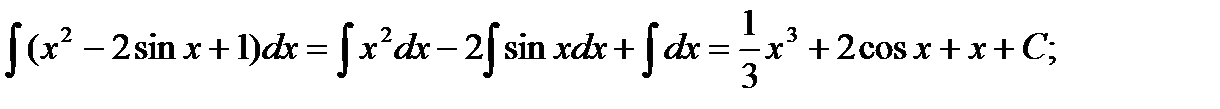
2. Самостоятельная работа
a) Для функции f найти первообразную, график которой проходит через точку М
f(x) = 4x + 1x2 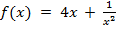 , M(-1; 4).
, M(-1; 4).
b) Найдите неопределённый интеграл:
1) 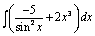 2)
2) 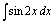 ; 3)
; 3) 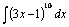 4.
4. 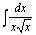
3. Домашнее задание: § 55, № 990, 992