Задание 1
Заданная передаточная функция:
Система уравнений общего вида:
Выражение 
называется характеристическим полиномом системы.
Запишем столбцовую присоединенную каноническую форму
А - матрица коэффициентов обратных связей, охватывающих интеграторы.
B - матрица коэффициентов связей входов модели и входов интеграторов.
C - матрица коэффициентов связей выходов интеграторов и выходов модели.
D - матрица коэффициентов связей входов и входов модели напрямую, минуя интеграторы
, 
, 
, D = [0]
tf([800 0],[1 15 30 80])
Cкалярная форма уравнений состояния запишется следующим образом:
Рисунок 1. Структурная схема модели в Simulink
Рисунок 2. Реакция на единичное ступенчатое воздействие.
Рисунок 3. Логарифмические амплитудная и фазовая частотные характеристики
Рисунок 4. Логарифмическая амплитудная частотная характеристика
Запишем строчную присоединенную каноническую форму
А - матрица коэффициентов обратных связей, охватывающих интеграторы.
B - матрица коэффициентов связей входов модели и входов интеграторов.
C - матрица коэффициентов связей выходов интеграторов и выходов модели.
D - матрица коэффициентов связей входов и входов модели напрямую, минуя интеграторы
, 
, 
, D = [0]
Cкалярная форма уравнений состояния запишется следующим образом:
Рисунок 5. Структурная схема модели в Simulink
Рисунок 6. Реакция на единичное ступенчатое воздействие
Рисунок 7. Логарифмические амплитудная и фазовая частотные характеристики
Рисунок 8. Логарифмические амплитудная характеристика
Имитация модели с помощью модального регулятора:
Модели с заданным характеристическим полином s^3 + 15 s^2 + 30 s + 80 формируем из цепочки интеграторов и обеспечиваем внешними обратными связями, т.е. модальным регулятором, встроенным в модель. Регулятор, состоящий из набора безынерционных обратных связей по переменным вектора состояния и формирующий управление u(t)= -k*x(t), называют модальным за его способность изменить все моды (собственные движения) системы 
. Здесь 
– вектор-строка параметров обратной связи.
Вводим модальным регулятором K, встроенным строкой в матрицу С
При отсутствии обратных связей внутри модели модальный регулятор K задаём коэффициентами характеристического полинома
K = [15 30 80]
Модальный регулятор позволяет полностью заменить характеристический полином некоторым желаемым. Для линейных систем управления все критерии оптимальности трансформируются в типовые размещения корней характеристического уравнения (полюсов передаточной функции замкнутой системы). Количество критериев оптимальности для систем управления невелико.
Типовые оптимальные решения представляются эталонными моделями, одно из решений соответствует случаю, когда все корни действительные и равные.
Подставляя u (t) = - k * x (t) в уравнения состояния, получим
где 
– матрица коэффициентов при переменных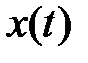 
замкнутой системы.
Для модели в строчной управляемой присоединённой канонической форме расчет строки K коэффициентов модального регулятора наиболее прост. Так как матрица B столбец из единицы и нулей, в матрице Az замкнутой модальным регулятором модели
Az = A – B*K
Действие модального регулятора можно интерпретировать как введение добавок в коэффициенты характеристического полинома (в обратные связи модели) для получения желаемых значений. Или как компенсацию имеющихся обратных связей и введение новых обратных связей, соответствующих желаемому полиному.
Модальный регулятор K вводим дополнительной 2-й строкой в матрицу С, т.е. c1=[c;K]
Квадратные скобки объединяют несколько матриц в одну. Разделителем столбцов является запятая.
Разделителем строк является точка с запятой.
c1 = 0 800 0
15 30 80
Рисунок 9. Структурная схема модального регулятора в Simulink
Разомкнутая модель с дополнительным выходом встроенного модального регулятора K
a = 0 0 0 b= 1 c = 0 0 800 d = 0
1 0 0 0 y K 15 30 80 y K 0
0 1 0 0
Передаточная функция разомкнутой модели:
y K= 
Cтрочная управляемая присоединённая форма после замыкания модели
a = x1 x2 x3 u
x1 -15 -30 -80 b= x1 1
x2 1 0 0 x2 0
x3 0 1 0 x3 0
c = x1 x2 x3
y model 0 800 0
y reg_K 15 30 80
d = u
y model 0
y reg_K 0
Изменилась 1-я строка матрицы A модели, определяющая характеристический полином.
Передаточная функция замкнутой модальным регулятором K модели:
y model: ------------------------
s^3 + 15 s^2 + 30 s + 80
15 s^2 + 30 s + 80
y reg ------------------------
s^3 + 15 s^2 + 30 s + 80