ОСНОВЫТЕОРИИ
Задача о движении системы тел в общем случае решается методами динамики. Для составления уравнения движения необходимо задать силы, действующие в системе. Однако в ряде случаев конечное состояние системы можно определить при помощи законов сохранения. В этих случаях нет необходимости знать все детали взаимодействия.
Закон сохранения импульса. В замкнутой системе тел полный импульс с течением времени не изменяется. Происходит лишь обмен импульсами между различными телами системы. На практике закон сохранения импульса применяется и в незамкнутых системах в следующих случаях.
1. Внешние силы малы и действуют короткое время, так что изменением импульса системы можно пренебречь.
2. Равна нулю проекция внешних сил на какое-либо направление. В этом случае сохраняется лишь соответствующая проекция импульса.
Закон сохранения энергии. Мерой изменения и превращения энергии в механике является работа. Если в системе действуют неконсервативные силы - силы трения, неупругой деформации,- то происходит превращение части механической энергии во внутреннюю. Работа внешних сил характеризует обмен энергией с другими системами.
Поэтому механическая энергия системы будет сохраняться если отсутствуют диссипативные процессы, (т.е. равна нулю работа неконсервативных сил), а также равна нулю работа внешних сил.
Импульс и кинетическая энергия системы. Пусть мы имеем систему материальных точек с массами mi, движущимися со скоростями vi в некоторой системе отсчета (ее называют лабораторной системой). Можно показать, что полный импульс системы определяется только скоростью движения центра масс v 0.:
p = å mi v i = m v 0, (1)
|
|
где m = å mi - полная масса системы.
Согласно теореме Кенига, кинетическая энергия системы может быть разложена на две составляющие:
T = T0 = Tотн. (2)
Первая составляющая T0 - это кинетическая энергия центра масс.
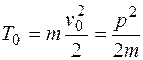. (3)
Вторая составляющая Tотн связана с движением частей системы относительно центра масс и называется энергией относительно движения
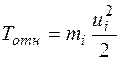, (4)
где ui = vi – v0 - скорости движения точек относительно центра масс (ее называют скоростью в системе центра масс).
В замкнутых системах вследствие сохранения импульса системы величина T0 остается неизменной. Изменения испытывает лишь кинетическая энергия относительного движения.
Удар шаров. Ударом называется изменение состояния тела вследствие кратковременного взаимодействия его с другим телом. Изменение импульса каждого тела Dpi за время Dt в соответствии со вторым законом Ньютона равно
Dpi = Fi Dt, (5)
где Fi - средняя за время Dt сила, действующая на тело.
Если система замкнута, между телами происходит лишь обмен импульсами. Полный же импульс системы остается неизменным.
В первой фазе удара силы деформации уравнивают скорости тел. Кинетическая энергия относительного движения на короткое время преобразуется в потенциальную энергию упругой деформации и частично - в энергию молекулярного движения (внутреннюю энергию).
Во второй фазе удара форма тел восстанавливается и потенциальная энергия вновь превращается в кинетическую (тела разлетаются).
Если деформации тел абсолютно упругие (форма тел восстанавливается полностью), то превращение механической энергии во внутреннюю отсутствует. При абсолютно неупругом ударе, напротив, отсутствует потенциальная энергия деформации: вся энергия относительного движения превращается во внутреннюю. Вторая фаза удара отсутствует, тела после удара не разлетаются.
|
|
Рассмотрим задачу об определении скоростей шаров v’1 и v’2 после центрального удара (рис.1).
Рис.1. Схема удара шаров.
При абсолютно упругом ударе система замкнута и отсутствуют неупругие деформации. Поэтому выполняются законы сохранения импульса и механической энергии. Сравнивая состояния до и после удара можно записать (необходимо учитывать знаки скоростей!).
(6)
. (7)
Решение этой системы уравнений позволяет вычислить скорости тел после удара v’1 и v’2.
При абсолютно неупругом ударе механическая энергия не сохраняется. Однако при этом тела не разлетаются и v’1 = v’2 = v’
m1v1 + m2v2 = (m1 + m2) v’. (8)
Для решения задачи о частично упругом ударе необходимо знать потери энергии, которые необходимо учесть соответствующим уравнением.
МЕТОДИКА ЭКСПЕРИМЕНТА.
Установка состоит из двух шаров, подвешенных на нитях длиной l (рис.2). Шар 1 перед ударом отклоняют, фиксируют при помощи электромагнита 3, а затем освобождают. На наклонном участке траектории под действием силы тяжести шар разгоняется.
Рис. 2. Схема установки.
Вблизи положения равновесия проекция внешних сил на горизонтальную ось равна нулю. Так как продолжительность удара мала, то в течение процесса столкновения шары находятся вблизи равновесного положения, поэтому при ударе происходит лишь обмен импульсами между шарами. Суммарный же импульс шаров не изменяется.
|
|
Скорость шара v в нижней точке можно вычислить по его отклонению при помощи закона сохранения энергии. В системе шар - гравитационное поле Земли действует консервативная сила тяжести. Сила натяжения нити работы не совершает. Поэтому на участке разгона потенциальная энергия шара в поле тяжести будет превращаться в его кинетическую энергию (рис. 2 б).
m v2 /2 = m g h, (9)
где h - высота подъема шара, связанная с его отклонением.
Тогда 
.
Высоту подъема шара и его скорость можно вычислить по отклонению (рис.2 б).
h = l - l·cosa = 2l·sin2(a /2),
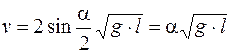. (10)
Здесь мы учли, что для малых углов sina » a. Такая же формула связывает скорость каждого шара и после удара с его последующим отклонением.
Импульс системы до столкновения равен
p = m1v. (11)
Кинетическая энергия центра масс системы равна
. (12)
Энергия относительного движения до столкновения будет равен
. (13)
Импульс системы после столкновения
. (14)
Энергия относительного движения после столкновения
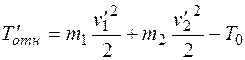. (15)
Коэффициент упругости удара можно определить как отношение энергий относительного движения после удара и до удара
h = T’отн / Tотн. (16)
Для абсолютно упругого удара h=1, для абсолютно неупругого h=0.
Логическая схема эксперимента.
1. Скорости и импульсы шаров в момент удара определяются по из отклонениям до или после удара в соответствии с законом сохранения энергии.
2. Изменяемая часть кинетической энергии определяется как кинетическая энергия в лабораторной системе координат минус энергия системы как целое (формулы (13) и (15)).
ВЫПОЛНЕНИЕ РАБОТЫ
1. Отцентрируйте шары. Линия, соединяющая центры шаров должна быть горизонтальной и параллельной направлению их движения. Поверхности шаров должны едва соприкасаться.
2. Отклонив правый шар на угол a1, произведите упругий удар. Измерьте a1 и a2 отклонения и после удара и время столкновения.
3. Повторите п.2 5 раз. Результаты занесите в табл. 1.
Таблица 1
| №№ | До удара | После удара | t, | ||
| п/п | a1, градус | a2, градус | a1, градус | a2, градус | мкс |
4. Выполните п.п 1-3 для неупругого удара, для этого на шар 2 нанесите слой пластилина. Результаты занесите в аналогичную таблицу.
5. Взвесьте шары. Результаты запишите в протокол.
ОБРАБОТКА РЕЗУЛЬТАТОВ
1. Проведите статистическую обработку результатов. Определите среднее значение и доверительную погрешность каждой из измеряемых величин a, a‘, t (относительную и абсолютную). Величины углов выразите в радианной мере.
2. Вычислите скорости и импульсы каждой пары шаров до и после удара для средних значений отклонения по формуле (10). Результаты занесите в табл. 2.
Таблица 2
| До удара | После удара | |||||
| ai, рад | vi, м/с | pi, кг м/с | a‘i, рад | v’i, м/с | p’i, кг м/с | |
| I шар m1..... | ||||||
| 2 шар m2..... |
3. Проверьте выполнение закона сохранения полного импульса системы шаров с учетом знаков.
p1 + p2 = p’1 + p’2.
Степень несовпадения вычислите по формуле
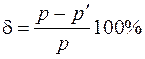
4. По формуле (5) определите силу удара для одного из опытов.
5. Выведите формулу для вычисления погрешности импульса через погрешности угла отклонения (по формулам погрешностей косвенных измерений).
Вычислите погрешности определения импульсов после удара для каждого шара Dp’1 и Dp’2.
6. Сформулируйте выводы. Сравните несовпадение импульсов с погрешностью измерений.
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ
Вычислите по формулам (12-15) кинетическую энергию центра масс, энергии относительного движения Тотн, и Т’отн, а также коэффициент упругости удара.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие законы сохранения выполняются при ударе шаров? Сформулируйте условия их выполнения.
2. Опишите превращения энергии в процессе удара. Какая часть энергии испытывает превращения?
3. На каком участке траектории в лабораторной установке выполняется закон сохранения импульса? На каком - не выполняется?
4. Как в эксперименте определяется скорость шара? Выведите формулу.
ЛИТЕРАТУРА
[1: §§ 25,27, 28]; [2: §§ 9, 12, 13, 15]; [5: § 14].