Тф 10-19 1 декабря
Преобразование Лапласа.
Отыскание оригиналов.


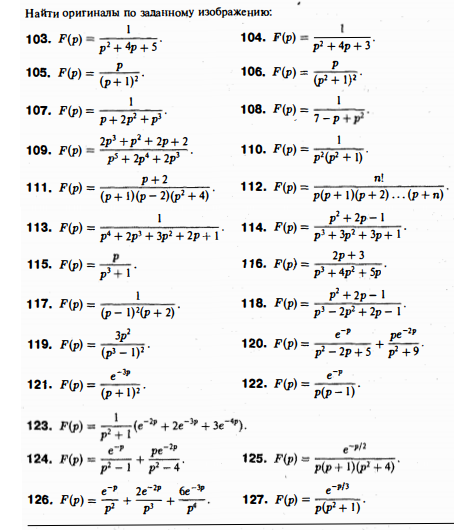



См далее

Можно воспользоваться свойством линейности и таблицей
Коэффициенты А,В, С находятся известным методом разложения правильной дроби на сумму простых дробей.






Как решить дифференциальное уравнение методом операционного исчисления?
На данном уроке будет подробно разобрана типовая и широко распространенная задача комплексного анализа – нахождение частного решения ДУ 2-го порядка с постоянными коэффициентами методом операционного исчисления. Снова и снова избавляю вас от предубеждения, что материал немыслимо сложный и недоступный. Забавно, но для освоения примеров можно вообще не уметь дифференцировать, интегрировать и даже не знать, что такое комплексные числа. Потребуется навык применения метода неопределённых коэффициентов, который детально разобран в статье Интегрирование дробно-рациональных функций. Фактически краеугольным камнем задания являются обычные алгебраические действия, и я уверен, что материал доступен даже для школьника.
Сначала сжатые теоретические сведения о рассматриваемом разделе математического анализа. Основная суть операционного исчисления состоит в следующем: функция действительной переменной 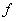 с помощью так называемого преобразования Лапласа отображается в функцию комплексной переменной с помощью так называемого преобразования Лапласа отображается в функцию комплексной переменной 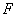 : : 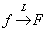 Терминология и обозначения: функция
Терминология и обозначения: функция 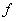 называется оригиналом; функция называется оригиналом; функция 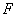 называется изображением; заглавной буквой называется изображением; заглавной буквой 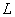 обозначается преобразование Лапласа.
Говоря простым языком, действительную функцию обозначается преобразование Лапласа.
Говоря простым языком, действительную функцию 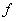 (оригинал) по определённым правилам нужно превратить в комплексную функцию (оригинал) по определённым правилам нужно превратить в комплексную функцию 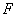 (изображение). Стрелочка (изображение). Стрелочка 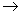 обозначает именно это превращение. А сами «определенные правила» и являются преобразованием Лапласа, которое мы рассмотрим лишь формально, чего для решения задач будет вполне достаточно.
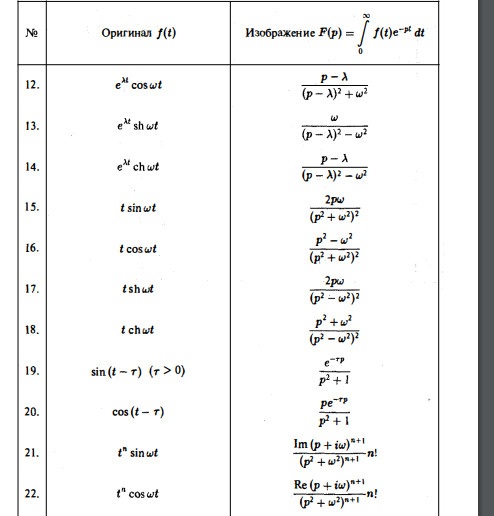
Осуществимо и обратное преобразование Лапласа, когда изображение превращается в оригинал: обозначает именно это превращение. А сами «определенные правила» и являются преобразованием Лапласа, которое мы рассмотрим лишь формально, чего для решения задач будет вполне достаточно.
Осуществимо и обратное преобразование Лапласа, когда изображение превращается в оригинал: 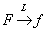 Зачем всё это нужно? В ряде задач высшей математики бывает очень выгодно перейти от оригиналов
Зачем всё это нужно? В ряде задач высшей математики бывает очень выгодно перейти от оригиналов 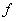 к изображениям к изображениям 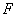 , поскольку в этом случае решение задания значительно упрощается (шутка). И как раз одну из таких задач мы и рассмотрим. Если вы дожили до операционного исчисления, то формулировка должна быть вам хорошо знакома:
Найти частное решение неоднородного уравнения второго порядка с постоянными коэффициентами , поскольку в этом случае решение задания значительно упрощается (шутка). И как раз одну из таких задач мы и рассмотрим. Если вы дожили до операционного исчисления, то формулировка должна быть вам хорошо знакома:
Найти частное решение неоднородного уравнения второго порядка с постоянными коэффициентами 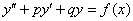 при заданных начальных условиях при заданных начальных условиях 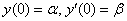 .
Примечание: иногда дифференциальное уравнение может быть и однородным: .
Примечание: иногда дифференциальное уравнение может быть и однородным: 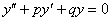 , для него в вышеизложенной формулировке также применим метод операционного исчисления. Однако в практических примерах однородное ДУ 2-го порядка встречается крайне редко, и далее речь пойдёт о неоднородных уравнениях.
Как известно, неоднородное дифференциальное уравнение 2-го порядка можно решить методом подбора частного решения по виду правой части либо методом вариации произвольных постоянных.
И сейчас будет разобран третий способ – решение ДУ с помощью операционного исчисления. Ещё раз подчеркиваю то обстоятельство, что речь идёт о нахождении частного решения, кроме того, начальные условия строго имеют вид , для него в вышеизложенной формулировке также применим метод операционного исчисления. Однако в практических примерах однородное ДУ 2-го порядка встречается крайне редко, и далее речь пойдёт о неоднородных уравнениях.
Как известно, неоднородное дифференциальное уравнение 2-го порядка можно решить методом подбора частного решения по виду правой части либо методом вариации произвольных постоянных.
И сейчас будет разобран третий способ – решение ДУ с помощью операционного исчисления. Ещё раз подчеркиваю то обстоятельство, что речь идёт о нахождении частного решения, кроме того, начальные условия строго имеют вид 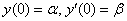 («иксы» равны нулям).
К слову, об «иксах». Уравнение («иксы» равны нулям).
К слову, об «иксах». Уравнение 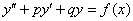 можно переписать в следующем виде: можно переписать в следующем виде: 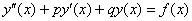 , где «икс» – независимая переменная, а «игрек» – функция. Я не случайно об этом говорю, поскольку в рассматриваемой задаче чаще всего используются другие буквы: , где «икс» – независимая переменная, а «игрек» – функция. Я не случайно об этом говорю, поскольку в рассматриваемой задаче чаще всего используются другие буквы:
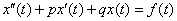 То есть роль независимой переменной играет переменная «тэ» (вместо «икса»), а роль функции играет переменная «икс» (вместо «игрека»)
Понимаю, неудобно конечно, но лучше придерживаться обозначений, которые встречаются в большинстве задачников и методичек.
Итак, наша задача с другими буквами записывается следующим образом:
Найти частное решение неоднородного уравнения второго порядка с постоянными коэффициентами
То есть роль независимой переменной играет переменная «тэ» (вместо «икса»), а роль функции играет переменная «икс» (вместо «игрека»)
Понимаю, неудобно конечно, но лучше придерживаться обозначений, которые встречаются в большинстве задачников и методичек.
Итак, наша задача с другими буквами записывается следующим образом:
Найти частное решение неоднородного уравнения второго порядка с постоянными коэффициентами 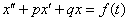 при заданных начальных условиях при заданных начальных условиях 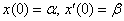 .
Смысл задания нисколько не изменился, изменились только буквы.
Как решить данную задачу методом операционного исчисления?
Прежде всего, потребуется таблица оригиналов и изображений. Это ключевой инструмент решения, и без неё не обойтись. Поэтому, по возможности, постарайтесь распечатать указанный справочный материал. Сразу же поясню, что обозначает буква «пэ»: комплексную переменную (вместо привычного «зет»). Хотя для решения задач этот факт не имеет особого значения, «пэ» так «пэ».
С помощью таблицы оригиналы .
Смысл задания нисколько не изменился, изменились только буквы.
Как решить данную задачу методом операционного исчисления?
Прежде всего, потребуется таблица оригиналов и изображений. Это ключевой инструмент решения, и без неё не обойтись. Поэтому, по возможности, постарайтесь распечатать указанный справочный материал. Сразу же поясню, что обозначает буква «пэ»: комплексную переменную (вместо привычного «зет»). Хотя для решения задач этот факт не имеет особого значения, «пэ» так «пэ».
С помощью таблицы оригиналы 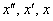 и и 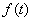 необходимо превратить в некоторые изображения. Далее следует ряд типовых действий, и используется обратное преобразование Лапласа (тоже есть в таблице). Таким образом, будет найдено искомое частное решение.
Все задачи, что приятно, решаются по достаточно жесткому алгоритму.
Пример 1
С помощью операционного исчисления найти частное решение дифференциального уравнения при заданных начальных условиях. необходимо превратить в некоторые изображения. Далее следует ряд типовых действий, и используется обратное преобразование Лапласа (тоже есть в таблице). Таким образом, будет найдено искомое частное решение.
Все задачи, что приятно, решаются по достаточно жесткому алгоритму.
Пример 1
С помощью операционного исчисления найти частное решение дифференциального уравнения при заданных начальных условиях. 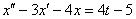 , , 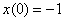 , , 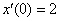 Решение: На первом шаге перейдем от оригиналов к соответствующим изображениям. Используем левую сторону таблицы оригиналов и изображений.
Сначала разбираемся с левой частью исходного уравнения. Для преобразования Лапласа справедливы правила линейности, поэтому все константы игнорируем и по отдельности работаем с функцией
Решение: На первом шаге перейдем от оригиналов к соответствующим изображениям. Используем левую сторону таблицы оригиналов и изображений.
Сначала разбираемся с левой частью исходного уравнения. Для преобразования Лапласа справедливы правила линейности, поэтому все константы игнорируем и по отдельности работаем с функцией 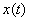 и её производными.
По табличной формуле №1 превращаем функцию: и её производными.
По табличной формуле №1 превращаем функцию: 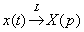 По формуле №2
По формуле №2 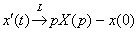 , учитывая начальное условие , учитывая начальное условие 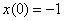 , превращаем производную: , превращаем производную: 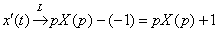 По формуле №3
По формуле №3 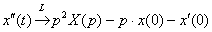 , учитывая начальные условия , учитывая начальные условия 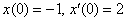 , превращаем вторую производную: , превращаем вторую производную: 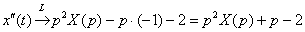 Не путаемся в знаках!
Признаюсь, правильнее говорить не «формулы», а «преобразования», но для простоты время от времени буду называть начинку таблицы формулами.
Теперь разбираемся с правой частью, в которой находится многочлен
Не путаемся в знаках!
Признаюсь, правильнее говорить не «формулы», а «преобразования», но для простоты время от времени буду называть начинку таблицы формулами.
Теперь разбираемся с правой частью, в которой находится многочлен 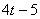 . В силу того же правила линейности преобразования Лапласа, с каждым слагаемым работаем отдельно.
Смотрим на первое слагаемое: . В силу того же правила линейности преобразования Лапласа, с каждым слагаемым работаем отдельно.
Смотрим на первое слагаемое: 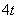 – это независимая переменная «тэ», умноженная на константу. Константу игнорируем и, используя пункт №4 таблицы, выполняем преобразование: – это независимая переменная «тэ», умноженная на константу. Константу игнорируем и, используя пункт №4 таблицы, выполняем преобразование: 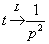 Смотрим на второе слагаемое: –5. Когда константа находится одна-одинёшенька, то пропускать её уже нельзя. С одиночной константой поступают так: для наглядности её можно представить в виде произведения:
Смотрим на второе слагаемое: –5. Когда константа находится одна-одинёшенька, то пропускать её уже нельзя. С одиночной константой поступают так: для наглядности её можно представить в виде произведения: 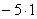 , а к единице применить преобразование: , а к единице применить преобразование: 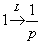 Таким образом, для всех элементов (оригиналов) дифференциального уравнения
Таким образом, для всех элементов (оригиналов) дифференциального уравнения 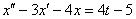 с помощью таблицы найдены соответствующие изображения: с помощью таблицы найдены соответствующие изображения: 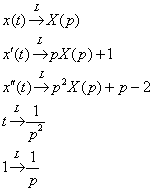 Подставим найденные изображения в исходное уравнение
Подставим найденные изображения в исходное уравнение 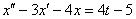 : : 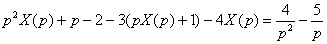 Дальнейшая задача состоит в том, чтобы выразить операторное решение
Дальнейшая задача состоит в том, чтобы выразить операторное решение 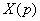 через всё остальное, а именно – через одну дробь. При этом целесообразно придерживаться следующего порядка действий:
Для начала раскрываем скобки в левой части: через всё остальное, а именно – через одну дробь. При этом целесообразно придерживаться следующего порядка действий:
Для начала раскрываем скобки в левой части: 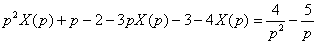 Приводим подобные слагаемые в левой части (если они есть). В данном случае складываем числа –2 и –3. Чайникам настоятельно рекомендую не пропускать данный этап:
Приводим подобные слагаемые в левой части (если они есть). В данном случае складываем числа –2 и –3. Чайникам настоятельно рекомендую не пропускать данный этап: 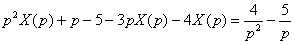 Слева оставляем слагаемые, в которых присутствует
Слева оставляем слагаемые, в которых присутствует 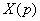 , остальные слагаемые переносим направо со сменой знака: , остальные слагаемые переносим направо со сменой знака: 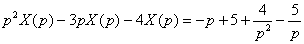 В левой части выносим за скобки операторное решение
В левой части выносим за скобки операторное решение 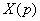 , в правой части приводим выражение к общему знаменателю: , в правой части приводим выражение к общему знаменателю: 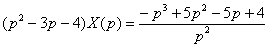 Многочлен слева следует разложить на множители (если это возможно). Решаем квадратное уравнение:
Многочлен слева следует разложить на множители (если это возможно). Решаем квадратное уравнение: 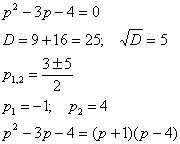 Таким образом:
Таким образом: 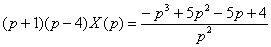 Сбрасываем
Сбрасываем 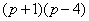 в знаменатель правой части: в знаменатель правой части: 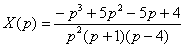 Цель достигнута – операторное решение
Цель достигнута – операторное решение 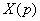 выражено через одну дробь.
Действие второе. Используя метод неопределенных коэффициентов, операторное решение уравнения следует разложить в сумму элементарных дробей: выражено через одну дробь.
Действие второе. Используя метод неопределенных коэффициентов, операторное решение уравнения следует разложить в сумму элементарных дробей: 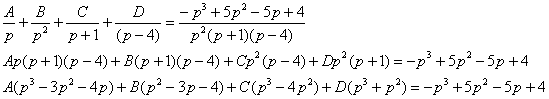 Приравняем коэффициенты при соответствующих степенях и решим систему:
Приравняем коэффициенты при соответствующих степенях и решим систему: 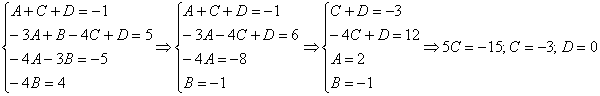 Если возникли затруднения с методом неопределенных коэффициентов, пожалуйста, наверстайте упущенное в статьях Интегрирование дробно-рациональной функции и Как решить систему уравнений? Это очень важно, поскольку разложение на дроби, по существу, самая важная часть задачи.
Итак, коэффициенты найдены:
Если возникли затруднения с методом неопределенных коэффициентов, пожалуйста, наверстайте упущенное в статьях Интегрирование дробно-рациональной функции и Как решить систему уравнений? Это очень важно, поскольку разложение на дроби, по существу, самая важная часть задачи.
Итак, коэффициенты найдены: 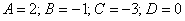 , и операторное решение предстаёт перед нами в разобранном виде: , и операторное решение предстаёт перед нами в разобранном виде: 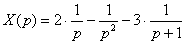 Обратите внимание, что константы записаны не в числителях дробей. Такая форма записи выгоднее, чем Обратите внимание, что константы записаны не в числителях дробей. Такая форма записи выгоднее, чем 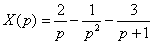 . А выгоднее, потому что финальное действие пройдёт без путаницы и ошибок:
Заключительный этап задачи состоит в том, чтобы с помощью обратного преобразования Лапласа перейти от изображений к соответствующим оригиналам. Используем правый столбец таблицы оригиналов и изображений.
Перейдем от изображений к соответствующим оригиналам: . А выгоднее, потому что финальное действие пройдёт без путаницы и ошибок:
Заключительный этап задачи состоит в том, чтобы с помощью обратного преобразования Лапласа перейти от изображений к соответствующим оригиналам. Используем правый столбец таблицы оригиналов и изображений.
Перейдем от изображений к соответствующим оригиналам:  Возможно, не всем понятно преобразование
Возможно, не всем понятно преобразование 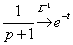 . Здесь использована формула пункта №5 таблицы: . Здесь использована формула пункта №5 таблицы: 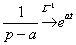 . Если подробнее: . Если подробнее: 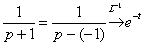 . Собственно, для похожих случаев формулу можно модифицировать: . Собственно, для похожих случаев формулу можно модифицировать: 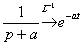 . Да и все табличные формулы пункта №5 очень легко переписать аналогичным образом.
После обратного перехода искомое частное решение ДУ получается на блюдечке с голубой каёмочкой:
Было: . Да и все табличные формулы пункта №5 очень легко переписать аналогичным образом.
После обратного перехода искомое частное решение ДУ получается на блюдечке с голубой каёмочкой:
Было: 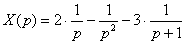 Стало:
Стало: 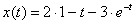 Ответ: частное решение:
Ответ: частное решение: 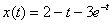 При наличии времени всегда желательно выполнять проверку. Проверка выполняется по стандартной схеме, которая уже рассматривалась на уроке Неоднородные дифференциальные уравнения 2-го порядка. Повторим:
Проверим выполнение начального условия
При наличии времени всегда желательно выполнять проверку. Проверка выполняется по стандартной схеме, которая уже рассматривалась на уроке Неоднородные дифференциальные уравнения 2-го порядка. Повторим:
Проверим выполнение начального условия 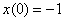 : : 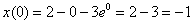 – выполнено.
Найдём первую производную: – выполнено.
Найдём первую производную: 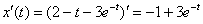 Проверим выполнение второго начального условия
Проверим выполнение второго начального условия 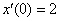 : : 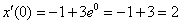 – выполнено.
Найдём вторую производную: – выполнено.
Найдём вторую производную: 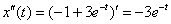 Подставим
Подставим 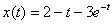 , , 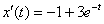 и и 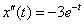 в левую часть исходного уравнения в левую часть исходного уравнения 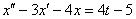 : : 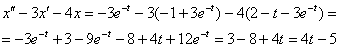 Получена правая часть исходного уравнения.
Вывод: задание выполнено правильно.
Небольшой пример для самостоятельного решения:
Пример 2
С помощью операционного исчисления найти частное решение дифференциального уравнения при заданных начальных условиях. Получена правая часть исходного уравнения.
Вывод: задание выполнено правильно.
Небольшой пример для самостоятельного решения:
Пример 2
С помощью операционного исчисления найти частное решение дифференциального уравнения при заданных начальных условиях. 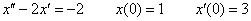 Примерный образец чистового оформления задания в конце урока.
Наиболее частный гость в дифференциальных уравнениях, как многие давно заметили, экспоненты, поэтому рассмотрим несколько примеров с ними, родными:
Пример 3
Найти частное решение дифференциального уравнения методом операционного исчисления.
Примерный образец чистового оформления задания в конце урока.
Наиболее частный гость в дифференциальных уравнениях, как многие давно заметили, экспоненты, поэтому рассмотрим несколько примеров с ними, родными:
Пример 3
Найти частное решение дифференциального уравнения методом операционного исчисления. 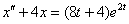 , , 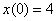 , , 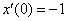 Решение: С помощью таблицы преобразований Лапласа (левая часть таблицы) перейдем от оригиналов к соответствующим изображениям.
Сначала рассмотрим левую часть уравнения. Там отсутствует первая производная. Ну и что из того? Отлично. Работы поменьше. Учитывая начальные условия
Решение: С помощью таблицы преобразований Лапласа (левая часть таблицы) перейдем от оригиналов к соответствующим изображениям.
Сначала рассмотрим левую часть уравнения. Там отсутствует первая производная. Ну и что из того? Отлично. Работы поменьше. Учитывая начальные условия 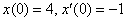 , по табличным формулам №№1,3 находим изображения: , по табличным формулам №№1,3 находим изображения: 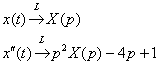 Теперь смотрим на правую часть:
Теперь смотрим на правую часть: 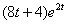 – произведение двух функций. Для того чтобы воспользоваться свойствами линейности преобразования Лапласа, нужно раскрыть скобки: – произведение двух функций. Для того чтобы воспользоваться свойствами линейности преобразования Лапласа, нужно раскрыть скобки: 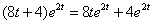 . Так как константы находятся в произведениях, то на них забиваем, и, используя группу №5 табличных формул, находим изображения: . Так как константы находятся в произведениях, то на них забиваем, и, используя группу №5 табличных формул, находим изображения: 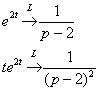 Подставим найденные изображения в исходное уравнение:
Подставим найденные изображения в исходное уравнение: 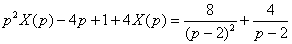 Напоминаю, что дальнейшая задача состоит в том, чтобы выразить операторное решение Напоминаю, что дальнейшая задача состоит в том, чтобы выразить операторное решение 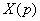 через единственную дробь.
В левой части оставляем слагаемые, в которых присутствует через единственную дробь.
В левой части оставляем слагаемые, в которых присутствует 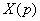 , остальные слагаемые переносим в правую часть. Заодно в правой части начинаем потихоньку приводить дроби к общему знаменателю: , остальные слагаемые переносим в правую часть. Заодно в правой части начинаем потихоньку приводить дроби к общему знаменателю: 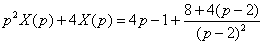 Слева выносим
Слева выносим 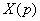 за скобки, справа приводим выражение к общему знаменателю: за скобки, справа приводим выражение к общему знаменателю: 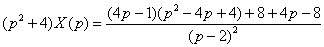 В левой части получен неразложимый на множители многочлен
В левой части получен неразложимый на множители многочлен 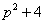 . Если многочлен не раскладывается на множители, то его, бедолагу, сразу нужно сбросить на дно правой части, . Если многочлен не раскладывается на множители, то его, бедолагу, сразу нужно сбросить на дно правой части, 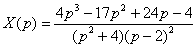 Наступил самый кропотливый этап: методом неопределенных коэффициентов разложим операторное решение уравнения в сумму элементарных дробей:
Наступил самый кропотливый этап: методом неопределенных коэффициентов разложим операторное решение уравнения в сумму элементарных дробей: 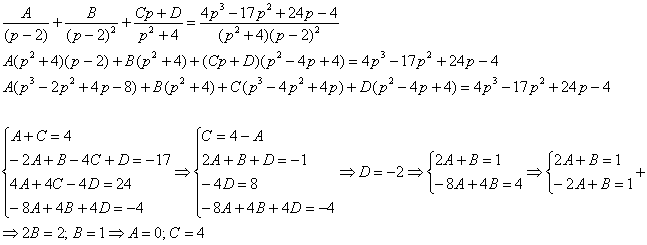 Таким образом: Таким образом: 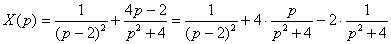 Обратите внимание, как разложена дробь:
Обратите внимание, как разложена дробь: 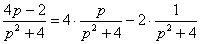 , скоро поясню, почему именно так.
Финиш: перейдем от изображений к соответствующим оригиналам, используем правый столбец таблицы: , скоро поясню, почему именно так.
Финиш: перейдем от изображений к соответствующим оригиналам, используем правый столбец таблицы:  В двух нижних преобразованиях использованы формулы №№6,7 таблицы, и дробь
В двух нижних преобразованиях использованы формулы №№6,7 таблицы, и дробь 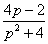 предварительно раскладывалась как раз для «подгонки» под табличные преобразования.
В результате, частное решение: предварительно раскладывалась как раз для «подгонки» под табличные преобразования.
В результате, частное решение: 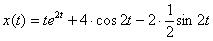 Ответ: искомое частное решение:
Ответ: искомое частное решение: 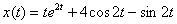 Похожий пример для самостоятельного решения:
Пример 4
Найти частное решение дифференциального уравнения методом операционного исчисления.
Похожий пример для самостоятельного решения:
Пример 4
Найти частное решение дифференциального уравнения методом операционного исчисления. 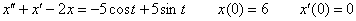 Краткое решение и ответ в конце урока.
В Примере 4 одно из начальных условий равно нулю. Это, безусловно, упрощает решение, и самый идеальный вариант, когда оба начальных условия нулевые:
Краткое решение и ответ в конце урока.
В Примере 4 одно из начальных условий равно нулю. Это, безусловно, упрощает решение, и самый идеальный вариант, когда оба начальных условия нулевые: 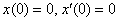 . В этом случае производные преобразуются в изображения без хвостов: . В этом случае производные преобразуются в изображения без хвостов: 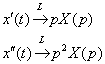 Как уже отмечалось, наиболее сложным техническим моментом задачи является разложение дроби методом неопределенных коэффициентов, и в моём распоряжении есть достаточно трудоёмкие примеры. Тем не менее, монстрами запугивать никого не буду, рассмотрим ещё пару типовых разновидностей уравнения:
Пример 5
Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
Как уже отмечалось, наиболее сложным техническим моментом задачи является разложение дроби методом неопределенных коэффициентов, и в моём распоряжении есть достаточно трудоёмкие примеры. Тем не менее, монстрами запугивать никого не буду, рассмотрим ещё пару типовых разновидностей уравнения:
Пример 5
Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. 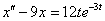 , , 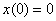 , , 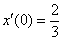 Решение: С помощью таблицы преобразований Лапласа перейдем от оригиналов к соответствующим изображениям. Учитывая начальные условия
Решение: С помощью таблицы преобразований Лапласа перейдем от оригиналов к соответствующим изображениям. Учитывая начальные условия 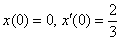 : : 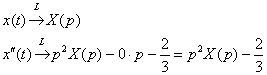 С правой частью тоже никаких проблем:
С правой частью тоже никаких проблем: 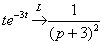 (Напоминаю, что константы-множители игнорируются)
Подставим полученные изображения в исходное уравнение и выполняем стандартные действия, которые, я надеюсь, вы уже хорошо отработали: (Напоминаю, что константы-множители игнорируются)
Подставим полученные изображения в исходное уравнение и выполняем стандартные действия, которые, я надеюсь, вы уже хорошо отработали: 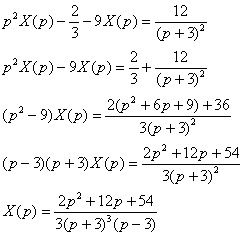 Константу в знаменателе выносим за пределы дроби, главное, потом про неё не забыть:
Константу в знаменателе выносим за пределы дроби, главное, потом про неё не забыть: 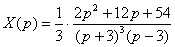 Думал, выносить ли ещё дополнительно двойку из числителя, однако, прикинув, пришел к выводу, что данный шаг практически не упростит дальнейшего решения.
Особенностью задания является полученная дробь. Кажется, что её разложение будет долгим и трудным, но впечатление обманчиво. Естественно, бывают сложные вещи, но в любом случае – вперёд, без страха и сомнений:
Думал, выносить ли ещё дополнительно двойку из числителя, однако, прикинув, пришел к выводу, что данный шаг практически не упростит дальнейшего решения.
Особенностью задания является полученная дробь. Кажется, что её разложение будет долгим и трудным, но впечатление обманчиво. Естественно, бывают сложные вещи, но в любом случае – вперёд, без страха и сомнений: 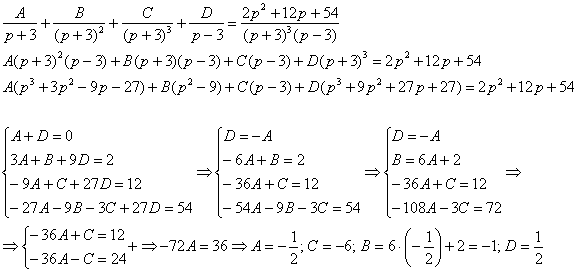 То, что некоторые коэффициенты получились дробными, смущать не должно, такая ситуация не редкость. Лишь бы техника вычислений не подвела. К тому же, всегда есть возможность выполнить проверку ответа.
В результате, операторное решение:
То, что некоторые коэффициенты получились дробными, смущать не должно, такая ситуация не редкость. Лишь бы техника вычислений не подвела. К тому же, всегда есть возможность выполнить проверку ответа.
В результате, операторное решение: 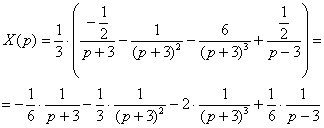 Перейдем от изображений к соответствующим оригиналам:
Перейдем от изображений к соответствующим оригиналам:  Таким образом, частное решение:
Таким образом, частное решение: 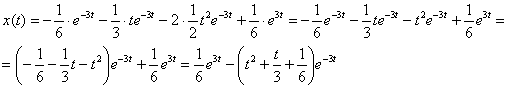 На последних двух шагах был проведён, так скажем, косметический ремонт ответа.
Ответ: частное решение:
На последних двух шагах был проведён, так скажем, косметический ремонт ответа.
Ответ: частное решение: 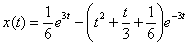 И, естественно, если в ходе решения получились дроби, то проверка напрашивается сама собой, чтобы развеять все сомнения относительно правильности результата. Я выполнил проверку на черновике, всё сошлось.
Похожий и весьма любопытный пример для самостоятельного решения:
Пример 6
Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
И, естественно, если в ходе решения получились дроби, то проверка напрашивается сама собой, чтобы развеять все сомнения относительно правильности результата. Я выполнил проверку на черновике, всё сошлось.
Похожий и весьма любопытный пример для самостоятельного решения:
Пример 6
Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. 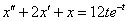 , , 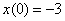 , , 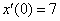 Он проще, чем кажется, решение и ответ в конце урока.
Рассматриваемые задания сплошь и рядом попадаются в контрольных работах, и я не случайно включаю в урок вроде бы однообразные примеры. В заключение разберу ещё один тип уравнения, который встречается реже, но встречается:
Пример 7
Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
Он проще, чем кажется, решение и ответ в конце урока.
Рассматриваемые задания сплошь и рядом попадаются в контрольных работах, и я не случайно включаю в урок вроде бы однообразные примеры. В заключение разберу ещё один тип уравнения, который встречается реже, но встречается:
Пример 7
Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. 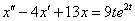 , , 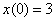 , , 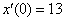 Алгоритм стандартен.
Решение: С помощью таблицы преобразований Лапласа перейдем от оригиналов к соответствующим изображениям:
Алгоритм стандартен.
Решение: С помощью таблицы преобразований Лапласа перейдем от оригиналов к соответствующим изображениям: 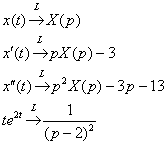 Подставим полученные изображения в исходное уравнение и выразим операторное решение:
Подставим полученные изображения в исходное уравнение и выразим операторное решение: 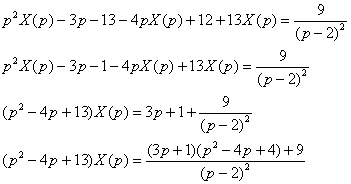 В левой части получен неразложимый на множители трёхчлен (можете попробовать решить квадратное уравнение). Подобный случай уже встречался в Примере 3. Ну не раскладывается, так не раскладывается, сбрасываем его в правую часть:
В левой части получен неразложимый на множители трёхчлен (можете попробовать решить квадратное уравнение). Подобный случай уже встречался в Примере 3. Ну не раскладывается, так не раскладывается, сбрасываем его в правую часть: 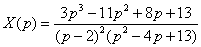 Методом неопределенных коэффициентов разложим операторное решение уравнения в сумму элементарных дробей:
Методом неопределенных коэффициентов разложим операторное решение уравнения в сумму элементарных дробей: 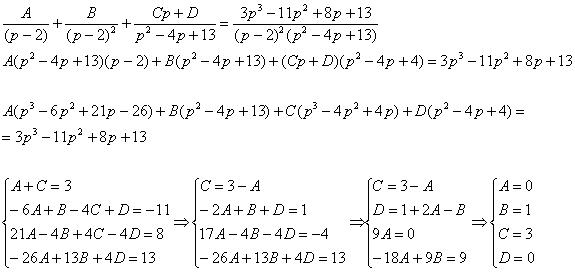 Таким образом:
Таким образом: 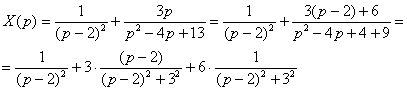 Пожалуйста, внимательно просмотрите на манипуляции с дробью
Пожалуйста, внимательно просмотрите на манипуляции с дробью 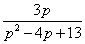 . Во-первых, в числителе использован искусственный приём: . Во-первых, в числителе использован искусственный приём: 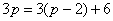 . Во-вторых, в знаменателе выделяется полный квадрат (если кто забыл о данном действии, читайте статью Интегрирование некоторых дробей). Все эти ухищрения выполнены с единственной целью: нужно преобразовать дробь . Во-вторых, в знаменателе выделяется полный квадрат (если кто забыл о данном действии, читайте статью Интегрирование некоторых дробей). Все эти ухищрения выполнены с единственной целью: нужно преобразовать дробь 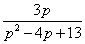 ТАК, чтобы потом использовать табличные формулы ТАК, чтобы потом использовать табличные формулы 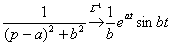 , , 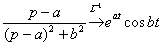 (№№10,11 таблицы).
Дальнейшее просто: (№№10,11 таблицы).
Дальнейшее просто:  В результате, частное решение:
В результате, частное решение: 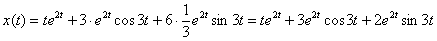 Ответ:
Ответ: 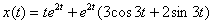 Как видите, помимо навыков решения, в рассмотренной задаче присутствует ещё и творчество. Когда происходит «затык», нужно постараться что-нибудь придумать, проявить смекалку, фантазию. Да и не только в математике.
Желаю успехов!
Решения и ответы:
Пример 2: Решение: С помощью таблицы преобразований Лапласа перейдем от оригиналов к соответствующим изображениям:
Как видите, помимо навыков решения, в рассмотренной задаче присутствует ещё и творчество. Когда происходит «затык», нужно постараться что-нибудь придумать, проявить смекалку, фантазию. Да и не только в математике.
Желаю успехов!
Решения и ответы:
Пример 2: Решение: С помощью таблицы преобразований Лапласа перейдем от оригиналов к соответствующим изображениям: 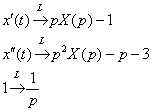 Подставим полученные изображения в исходное уравнение: Подставим полученные изображения в исходное уравнение: 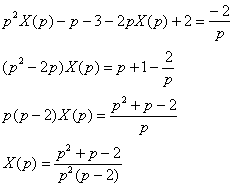 Методом неопределенных коэффициентов разложим операторное решение уравнения в сумму элементарных дробей: Методом неопределенных коэффициентов разложим операторное решение уравнения в сумму элементарных дробей: 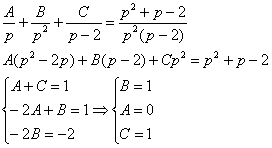 Таким образом: Таким образом: 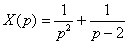 Перейдем от изображений к соответствующим оригиналам: Перейдем от изображений к соответствующим оригиналам: 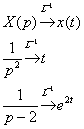 Ответ: частное решение: Ответ: частное решение: 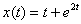 Пример 4:Решение: С помощью таблицы преобразований Лапласа перейдем от оригиналов к соответствующим изображениям:
Пример 4:Решение: С помощью таблицы преобразований Лапласа перейдем от оригиналов к соответствующим изображениям: 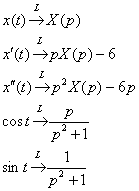 Подставим полученные изображения в исходное уравнение: Подставим полученные изображения в исходное уравнение: 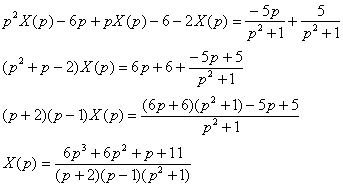 Методом неопределенных коэффициентов разложим операторное решение уравнения в сумму элементарных дробей: Методом неопределенных коэффициентов разложим операторное решение уравнения в сумму элементарных дробей: 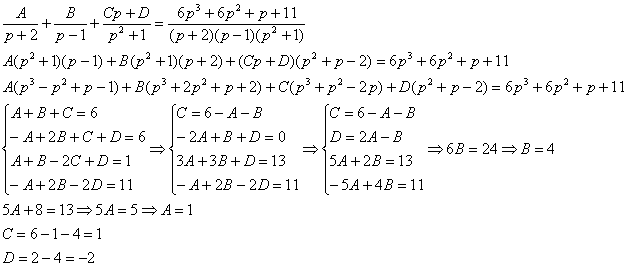 Таким образом:
Таким образом: 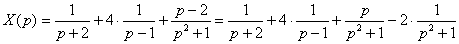 Перейдем от изображений к соответствующим оригиналам: Перейдем от изображений к соответствующим оригиналам:  Ответ: частное решение: Ответ: частное решение: 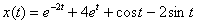 Пример 6: Решение: С помощью таблицы преобразований Лапласа перейдем от оригиналов к соответствующим изображениям. Учитывая начальные условия
Пример 6: Решение: С помощью таблицы преобразований Лапласа перейдем от оригиналов к соответствующим изображениям. Учитывая начальные условия 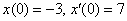 : : 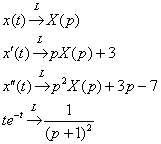 Подставим полученные изображения в исходное уравнение: Подставим полученные изображения в исходное уравнение: 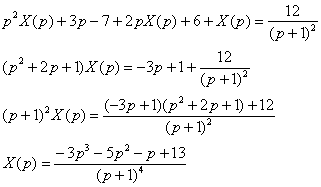 Методом неопределенных коэффициентов получим сумму дробей: Методом неопределенных коэффициентов получим сумму дробей: 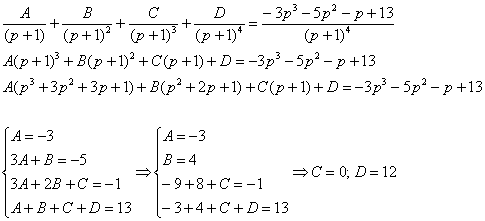 В результате: В результате: 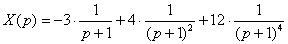 Перейдем от изображений к соответствующим оригиналам: Перейдем от изображений к соответствующим оригиналам:  Частное решение: Частное решение: 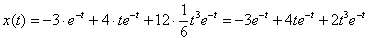 Ответ: Ответ: 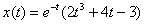 Автор: Емелин Александр
Автор: Емелин Александр
  Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
 Профессиональная помощь по любому предмету – Zaochnik.com Профессиональная помощь по любому предмету – Zaochnik.com
|
| © Copyright mathprofi.ru, Александр Емелин, 2010-2020. Копирование материалов сайта запрещено |