Основные формулы и теоремы теории случайных событий

1.2.1. Теоремы сложения и умножения вероятностей

Различные отношения между событиями влекут за собой определенные соотношения между их вероятностями. Сформулируем так называемые теоремы сложения вероятностей.

Теорема 1. Если события 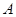и 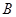являются несовместными, то вероятность появления одного из них в данном испытании равна сумме их вероятностей, то есть

.

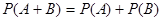Принцип распространяется на любое конечное число попарно несовместных событий, то есть если для всяких 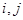справедливо, что события 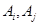несовместны, то

.

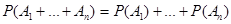Важным следствием этой теоремы является следующее равенство

.

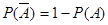Теорема 2. Если события 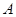и 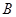являются совместными, то вероятность появления хотя бы одного из них в данном испытании равна сумме их вероятностей без вероятности их совместного наступления, то есть

.

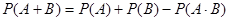Определение. События 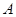и 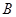называются зависимыми, если вероятность каждого из них зависит от того, произошло другое событие или нет. В противном случае события называются независимыми. События 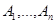называются независимыми в совокупности, если вероятность каждого из них не зависит от того, произошли остальные или нет.

Вероятность события 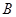, вычисленная в предположении, что событие 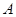уже произошло, называется условной вероятностью события 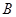и обозначается .

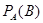Сформулируем теоремы умножения вероятностей.

Теорема 3. Вероятность совместного появления независимых событи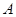й и 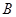равна произведению их вероятностей, то есть

.

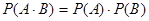Теорема распространяется на случай любого конечного числа независимых в совокупности событий.

Теорема 4. Вероятность совместного появления зависимых событи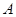й и 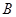равна произведению вероятности одного из них на условную вероятность другого, то есть

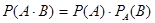или .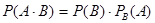

Вероятность совместного наступления конечного числа 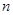зависимых событий 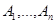равна произведению вероятности одного из них на условные вероятности всех остальных, причем условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже наступили, то есть

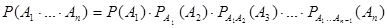
1.2.2. Формула полной вероятности и формула Байеса.

Следствием правил вычисления вероятностей суммы и произведения событий являются формула полной вероятности и формула Байеса.

Пусть некоторое событие А может наступить лишь при условии наступления только одного из событий 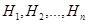, называемых гипотезами, причем никакие два из них не могут произойти одновременно, но одно обязательно произойдет в результате испытания, то есть 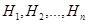образуют полную группу несовместных событий. Обозначим 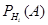- вероятность наступления события А при условии, что событие 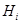уже произошло. Тогда вероятность наступления события А определяется по формуле полной вероятности:

.

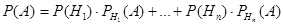Если событие А уже произошло и требуется переоценить вероятности гипотез в связи с наступлением события А, то используется формула Байеса (Томас Байес, 1702-1761):

,

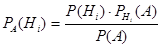где Р (А) определяется по формуле полной вероятности. Формулу Байеса еще называют теоремой гипотез. При этом условную вероятность 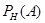называют доопытной (априорной), а 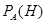- послеопытной (апостериорной) условной вероятностью.

Решение задач с помощью данных формул и теорем будет рассмотрено на практических занятиях.

1.2.3. Схема Бернулли проведения независимых испытаний

В задачах теории вероятностей распространена некоторая типичная ситуация, которую принято называть схемой Бернулли (схемой независимых испытаний).

Пусть проводится серия из 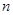независимых испытаний, в каждом из которых некоторое событие 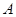может наступить с одной и той же вероятностью 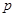. Формула Бернулли (Яков Бернулли, 1654-1705) позволяет определить вероятность того, что событие 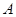наступит в рассматриваемой серии испытаний ровно 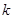раз.

Пусть 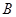– событие, состоящее в том, что 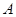наступит k раз, тогда

,

где .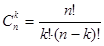

В случае, если число испытаний велико вместо формулы Бернулли используются приближенные формулы.

Предельная теорема Пуассона.

Будем считать, что проводится достаточно длинная серия независимых испытаний, в каждом из которых появление некоторого события маловероятно. Тогда оценку для 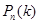дает предельная теорема Пуассона (Симеон Дени Пуассон, 1781 – 1840), называемая еще законом редких явлений.

Теорема. При приближении вероятности 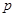к нулю справедливо равенство

.

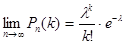Следствием теоремы являются приближенные формулы:

,

,

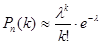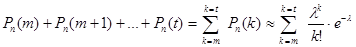при использовании которых полагаем, что 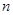достаточно велико, а вероятность 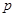мала и параметр находим по формуле .

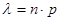Для выражения 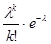, рассматриваемого в качестве функции двух аргументов 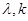, составлена таблица значений.

Локальная теорема Лапласа.

Проводится серия из 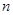независимых испытаний, в каждом из которых вероятность появления события 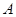постоянна и равна 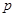. Тогда вероятность того, что в этой серии 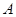наступит ровно 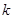раз, может быть определена по приближенной формуле

,

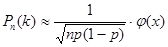где , .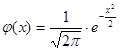

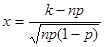Формула дает достаточно точное значение вероятности, если .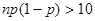

Функция 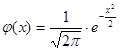является четной, она табулирована, значения для положительных аргументов приведены в специальной таблице.

Интегральная теорема Лапласа.

Проводится серия из 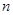независимых испытаний, в каждом из которых вероятность появления события 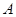постоянна и равна 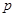. Тогда вероятность того, что в этой серии событие 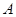наступит не менее 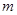и не более 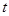раз, может быть найдена по приближенной формуле

,

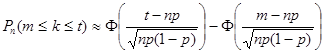где 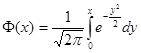- (стандартизированная) функция Лапласа.

Формула дает достаточно точное значение, если 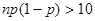. Функция Лапласа нечетная, табулирована, значения для положительных аргументов можно найти в приложении 3. Для 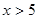полагаем, что .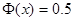