Введение
Решение систем линейных алгебраических уравнений – одна из основных задач вычислительной линейной алгебры. Хотя задача решения системы линейных уравнений сравнительно редко представляет самостоятельный интерес для приложений, от умения эффективно решать такие системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ. Значительная часть численных методов решения различных (в особенности – нелинейных) задач включает в себя решение систем линейных уравнений как элементарный шаг соответствующего алгоритма.
Одна из трудностей практического решения систем большой размерности связанна с ограниченностью оперативной памяти ЭВМ. Хотя обьем оперативной памяти вновь создаваемых вычислительных машин растет очень быстро, тем не менее, еще быстрее возрастают потребности практики в решении задач все большей размерности. В значительной степени ограничения на размерность решаемых систем можно снять, если использовать для хранения матрицы внешние запоминающие устройства. Однако в этом случае многократно возрастают как затраты машинного времени, так и сложность соответствующих алгоритмов. Поэтому при создании вычислительных алгоритмов линейной алгебры большое внимание уделяют способам компактного размещения элементов матриц в памяти ЭВМ.
К счастью, приложения очень часто приводят к матрицам, в которых число ненулевых элементов много меньше общего чила элементов матрицы. Такие матрицы принято называть разреженными. Одним из основных источников разреженных матриц являются математические модели технических устройств, состоящих из большого числа элементов, связи между которыми локальны. Простейшие примеры таких устройств – сложные строительные конструкции и большие электрические цепи.
Известны примеры решенных в последние годы задач, где число неизвестных достигало сотен тысяч. Естественно, это было бы невозможно, если бы соответствующие матрицы не являлись разреженными (матрица системы из 100 тыс. уравнений в формате двойной точности заняла бы около 75 Гбайт).
Решение систем линейных уравнений с помощью определений
1.1. Определители второго и третьего порядка
Рассмотрим определители второго и третьего порядков, их свойства. А также теорему Крамера, позволяющую решать системы линейных уравнений с помощью определителей. Определители используются также в дальнейшем в теме "Векторная алгебра" при вычислении векторного произведения векторов.
Определители второго и третьего порядка.
Рассмотрим таблицу из четырех чисел вида: 
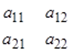
Числа в таблице обозначены буквой с двумя индексами. Первый индекс указывает номер строки, второй – номер столбца.
Определение 1. Определителем второго порядка называют выражение вида:
Числа а11, …, а22 называют элементами определителя.
Диагональ, образованная элементами а11; а22 называется главной, а диагональ, образованная элементами а12; а21 - побочной.
Таким образом, определитель второго порядка равен разности произведений элементов главной и побочной диагоналей.
Заметим, что в ответе получается число.
Примеры. Вычислить:
Рассмотрим теперь таблицу из девяти чисел, записанных в три строки и три столбца:
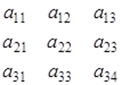
Определение 2. Определителем третьего порядка называется выражение вида:
Элементы а11; а22; а33 – образуют главную диагональ.
Числа а13; а22; а31 – образуют побочную диагональ.
Изобразим, схематически, как образуются слагаемые с плюсом и с минусом:
С плюсом входят: произведение элементов на главной диагонали, остальные два слагаемых являются произведением элементов, расположенных в вершинах треугольников с основаниями, параллельными главной диагонали.
Слагаемые с минусом образуются по той же схеме относительно побочной диагонали.
Это правило вычисления определителя третьего порядка называют:
Правилом треугольников.
Примеры. Вычислить по правилу треугольников:
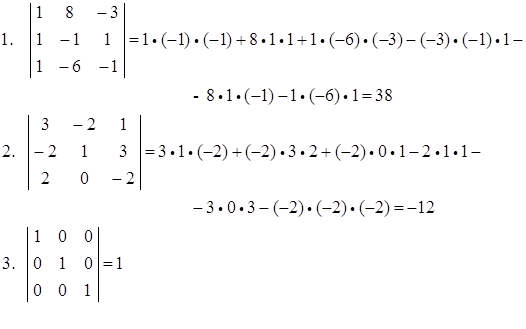
Определители называют также детерминантами.
1.2. Свойства определителей. Теорема разложения. Теорема Крамера.
Приведенные далее свойства выполняются для определителей любого порядка. Все они могут быть доказаны непосредственной проверкой, основанной на правилах вычисления определителей.
Свойство 1. Величина определителя не изменится, если его строки поменять местами с соответствующими столбцами.
.
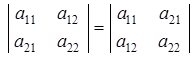Раскрывая оба определителя, убеждаемся в справедливости равенства.
Свойство 1 устанавливает равноправность строк и столбцов определителя. Поэтому все дальнейшие свойства определителя будем формулировать и для строк и для столбцов.
Свойство 2. При перестановке двух строк (или столбцов) определитель изменяет знак на противоположный, сохраняя абсолютную величину.
.
Свойство 3. Общий множитель элементов строки (или столбца) можно выносить за знак определителя.
.
Свойство 4. Если определитель имеет две одинаковые строки (или столбца), то он равен нулю.
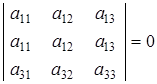
Это свойство можно доказать непосредственной проверкой, а можно использовать свойство 2.
Обозначим определитель за D. При перестановке двух одинаковых первой и второй строк он не изменится, а по второму свойству он должен поменять знак, т.е.
D = - DÞ 2 D = 0 ÞD = 0.
Свойство 5. Если все элементы какой–то строки (или столбца) равны нулю, то определитель равен нулю.
Это свойство можно рассматривать как частный случай свойства 3 при,
k = 0
Свойство 6. Если элементы двух строк (или столбцов) определителя пропорциональны, то определитель равен нулю.
.
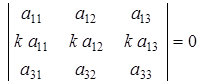Можно доказать непосредственной проверкой или с использованием свойств 3 и 4.
Свойство 7. Величина определителя не изменится, если к элементам какой-либо строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число.
.
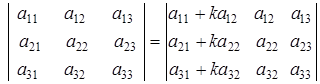Доказывается непосредственной проверкой.
Применение указанных свойств может в ряде случаев облегчить процесс вычисления определителей, особенно третьего порядка.
Для дальнейшего нам понадобится понятия минора и алгебраического дополнения. Рассмотрим эти понятия для определения третьего порядка.
Определение 3. Минором данного элемента определителя третьего порядка называется определитель второго порядка, полученный из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
Минор элемента аij обозначается Мij. Так для элемента а11 минор
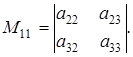
Он получается, если в определителе третьего порядка вычеркнуть первую строку и первый столбец.
Определение 4. Алгебраическим дополнением элемента определителя называют его минор, умноженный на (-1)k, где k – сумма номеров строки и столбца, на пересечении которых стоит данный элемент.
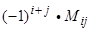Алгебраическое дополнение элемента аij обозначается Аij.
Таким образом, А i j =
Выпишем алгебраические дополнения для элементов а11 и а12.
.
.
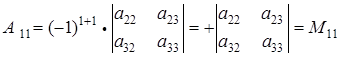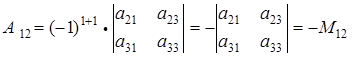Полезно запомнить правило: алгебраическое дополнение элемента определителя равно его минору со знаком плюс, если сумма номеров строки и столбца, в которых стоит элемент, четная, и со знаком минус, если эта сумма нечетная.
Пример. Найти миноры и алгебраические дополнения для элементов первой строки определителя:
Миноры:
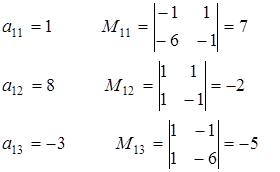
| Алгебраические дополнения:
|
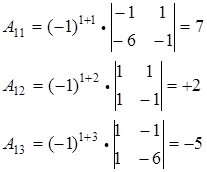
Ясно, что миноры и алгебраические дополнения могут отличаться только знаком.
Рассмотрим без доказательства важную теорему – теорему разложения определителя.
ТЕОРЕМА РАЗЛОЖЕНИЯ
Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения.
Используя эту теорему, запишем разложение определителя третьего порядка по первой строке.
.
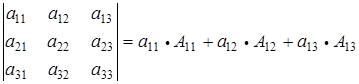В развернутом виде:
.
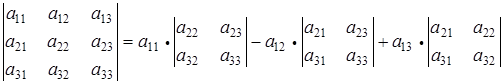Последнюю формулу можно использовать как основную при вычислении определителя третьего порядка.
Теорема разложения позволяет свести вычисление определителя третьего порядка к вычислению трех определителей второго порядка.
Рекомендуется раскладывать определитель по той строке или столбцу, где есть нули, т.к. для нулевых элементов не надо находить алгебраические дополнения.
Теорема разложения дает второй способ вычисления определителей третьего порядка.
Примеры. Вычислить определитель, используя теорему разложения.
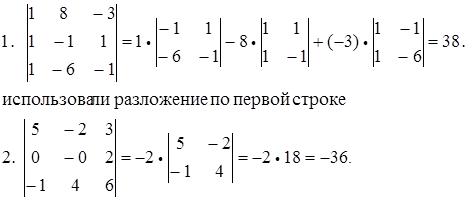
использовали разложения по второй строке.
Теорема разложения позволяет также вычислять определители более высокого порядка, сводя их к вычислению нескольких определителей третьего или второго порядка.
Так, определитель четвертого порядка можно свести к вычислению четырех определителей третьего порядка.
ТЕОРЕМА КРАМЕРА
Применим рассмотренную теорию определителей к решению систем линейных уравнений.
1. Система двух линейных уравнений с двумя неизвестными.
Здесь х1, х2 – неизвестные;
А11, …, а22 – коэффициенты при неизвестных, занумерованные двумя индексами, где первый индекс означает номер уравнения, а второй индекс – номер неизвестного.
b1, b2 – свободные члены.
Напомним, что под решением системы понимается пара значений х1, х2, которые при подстановке в оба уравнения обращают их в верные равенства.
В случае, когда система имеет единственное решение, это решение можно найти с помощью определителей второго порядка.
Определение 5. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы.
Обозначим определитель системы D.
D =
.
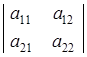
В столбцах определителя D стоят коэффициенты соответственно при х1 и при, х2.
Введем два дополнительных определителя, которые получаются из определителя системы заменой одного из столбцов столбцом свободных членов:
D1 =
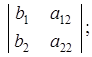
D2 =
.
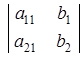Рассмотрим без доказательства следующую теорему:
ТЕОРЕМА КРАМЕРА (для случая n = 2)
Если определитель D системы (3) отличен от нуля (D¹0), то система имеет единственное решение, которое находится по формулам:
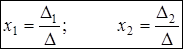
(4)
Формулы (4) называются формулами Крамера.
ПРИМЕР. Решить систему по правилу Крамера.
.
Ответ: х 1 = 3; х 2 = -1
2. Система трех линейных уравнений с тремя неизвестными:
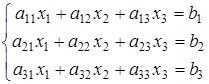(5)
В случае единственного решения систему (5) можно решить с помощью определителей третьего порядка.
Определитель системы D имеет вид:
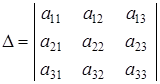
Введем три дополнительных определителя:
.
Аналогично формулируется теорема.
ТЕОРЕМА КРАМЕРА (для случая n = 3)
Если определитель D системы (5) отличен от нуля, то система имеет единственное решение, которое находится по формулам:
|
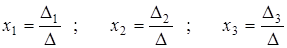
(6)
Формулы(6) – это формулы Крамера.
ЗАМЕЧАНИЕ. Г. Крамер (1704 – 1752) – швейцарский математик.
Заметим, что теорема Крамера применима, когда число уравнений равно числу неизвестных и когда определитель системы D отличен от нуля.
Если определитель системы равен нулю, то в этом случае система может либо не иметь решений, либо иметь бесчисленное множество решений. Эти случаи исследуются особо, с ними можно подробно познакомиться в рекомендуемой литературе.
Отметим только один случай:
Если определитель системы равен нулю (D = 0), а хотя бы один из дополнительных определителей отличен от нуля, то система решений не имеет (т.е. является несовместной).
Теорему Крамера можно обобщать для системы n линейных уравнений с n неизвестными.
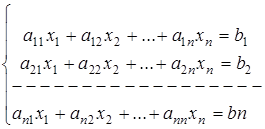
Если
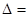
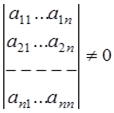
,то единственное решение системы находится по формулам Крамера:
Дополнительный определитель
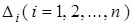
получается из определителя D, если в нем столбец коэффициентов при неизвестном
xi заменить столбцом свободных членов.
Заметим, что определители D, D1, …, Dn имеют порядок n.
Заключение
В реферате рассмотрено понятие – определитель, подробно рассмотрены определители второго и третьего порядков, часто встречающиеся на практике. Для определителя третьего порядка приводятся два способа вычисления. Рассмотрена теорема Крамера, которая дает практический способ решения систем линейных уравнений, для случая, когда решение единственное. Более подробно с этой темой можно познакомиться в рекомендуемой литературе.
Список использованной литературы
1. Гармаш А.Н. Математические методы в управлении: учеб. пособие / А. Н. Гармаш, И. В. Орлова; ВЗФЭИ. - М.: Вузовский учебник: ИНФРА-М, 2012. - 272 с.;
2. Какзанова Е.М. Терминологический энциклопедический словарь: Математика и всё, что с ней связано, на немецком, английском и русском языках / Е. М. Какзанова. - М.: Астрель: АСТ, 2009. - 479 с.;
3. Малугин, В. А. Математический анализ для экономического бакалавриата: учебник и практикум / В. А. Малугин. – 3-e изд., перераб. и доп. – М.: Юрайт, 2013. – 557 с.;
4. Математический анализ:учебно-методическое пособие/МОиН РФ, ГОУ ВПО Кемеровский государственный универс; [сост.: А. М. Вайнгауз, В. А. Геллерт].-Томск:издательство ТГПУ. Ч. 1.-2008.-76 с.;
5. https://ru.wikipedia.org/