ФОРМИРОВАНИЕ ПОГРЕШНОСТИ В ИЗМЕРИТЕЛЬНОМ КАНАЛЕ
ПОГРЕШНОСТЬ ИЗМЕРЕНИЯ
Результат измерения физической величины, полученный с помощью любого технического средства, всегда отличается от ее истинного значения на величину, называемую погрешностью измерения
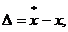
где 
– абсолютное значение погрешности; 
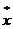– результат измерения; x – истинное значение измеряемой величины. Наличие погрешности вызвано тем, что реальная функция преобразования измерительного прибора или преобразователя отличается от номинальной.
Простота и ясность представления погрешности однократного измерения как абсолютной разности результата измерения и истинного значения физической величины сочетаются с многообразием характера связей ее конкретного числового значения с большим числом определяющих факторов. Среди них основными являются принцип работы средства измерения (СИ), условия его эксплуатации, параметры объекта измерения, истинное значение измеряемой физической величины. При этом погрешность может рассматриваться как функция самой измеряемой величины, времени или параметров ОИ и СИ. Общепринятые классификационные признаки и их связь с погрешностями приведены в табл. 1.1. Они характеризуют свойства самих погрешностей, порождающие их причины и формы представления.
Форма представления погрешности
Абсолютное значение погрешностиD без указания интервала значений измеряемой величины, для которого оно было получено, ничего не говорит о метрологических характеристиках СИ. Чаще пользуются ее относительным значением
.
Таблица 1.1. Классификация погрешности
| № | Классификационный признак | Классификация | ||||
| Форма представления погрешности | Абсолютная погрешность | Относительная погрешность | Приведенная погрешность | |||
| Условия применения средства измерения | Основная погрешность | Дополнительная погрешность | ||||
| Характер связи с измеряемой величиной | Отсутствие связи (аддитивная) | Линейная функция связи (линейная мультипликативная) | Произвольная функция связи | |||
| Источник возникновения | Инструментальная | Методическая | ||||
| Зависимость от динамических характеристик измеряемой величины | Статическая погрешность | Динамическая погрешность из-за конечного времени измерения | Динамическая погрешность из-за инерционности | |||
| Характер проявления при многократных измерениях | Некоррелированная на интервале наблюдения случайная величина | Коррелированная на интервале наблюдения случайная величина | Постоянная величина | |||
Относительная погрешность 
имеет существенный недостаток. Она резко возрастает в начале диапазона, поэтому удобнее приводить D к постоянной величине, например верхней границе диапазона. Такая погрешность называется приведенной:
,
где 
– нормирующее значение, равное большему из пределов измерений.
Очевидно, что приведенная погрешность равна возможному наименьшему значению относительной погрешности конкретного СИ. Обычно относительная и приведенная погрешности выражаются в процентах.
Условия применения СИ
Основной погрешностью называется погрешность, свойственная СИ при работе в нормальных условиях, оговоренных стандартами или техническими условиями. Дополнительная погрешность появляется при отклонении условий эксплуатации от нормальных. Зависимость метрологической характеристики СИ от изменения влияющей величины в пределах рабочих условий эксплуатации описывается функцией влияния, задаваемой в виде формулы, таблицы или графика.
Характер связи с измеряемой величиной
В общем случае погрешность СИ зависит от измеряемой величины. Характер зависимости определяется отличием реальной функции преобразования 
от идеальной 
. Общепринятым является разделение погрешностей на аддитивные и мультипликативные. Аддитивными называют погрешности, остающиеся постоянными внутри диапазона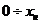 
, т. е. не зависящие от истинного значения измеряемой величины (рис. 1.1,а). Погрешность, изменяющуюся по закону 
, называют линейной мультипликативной (рис. 1.1,б). В случае нелинейной функции связи ∆ = f (x) погрешность является нелинейной мультипликативной (рис. 1.1,в). Существуют специфические виды погрешностей, например погрешность квантования 
, связанная с истинным значением величины x заранее известной зависимостью — кусочно-линейной функцией
(рис. 1.2,а). По определению такая погрешность является мультипликативной. Погрешность СИ, реализующего процесс аналого-цифрового преобразования, является случайной, так как в интервале между двумя соседними дискретными значениями невозможно более точно оценить истинное значение x. В пределах кванта дискретной шкалы 
все значения равновероятны, поэтому погрешность квантования распределена по равномерному закону (рис. 1.2,б).
а б в
Рис. 1.1. Аддитивная и мультипликативные погрешности
а б
Рис. 1.2. Погрешность квантования
Таким образом, при детерминированном характере зависимости 
погрешность результата преобразования конкретного значения аналоговой величины x является случайной.
Источник возникновения
Составляющая погрешности измерений, обусловленная точностью применяемых средств измерения, называется инструментальной погрешностью. Она определяется конструктивными и технологическими особенностями СИ, качеством и стабильностью элементов системы, используемыми методом и принципом измерения. Инструментальная погрешность зависит только от метрологических характеристик СИ.
Присутствие в суммарной погрешности другой составляющей, называемой методической, может вызываться разнообразными причинами. Это неадекватность модели реальному объекту измерения, выражающаяся в пренебрежении влиянием неинформативных параметров среды на результат измерения, упрощении связей между физическими переменными при совместных или совокупных измерениях. Другой причиной методических погрешностей является идеализация отношений в системе ОИ – СИ. Погрешности возникают из-за конечной величины эквивалентных сопротивлений линий связи между ОИ и СИ, переходных сопротивлений средств коммутации, энергетического обмена в обоих направлениях при передаче сигнала — носителя измерительной информации. При этом на результат измерения оказывают влияние внутреннее сопротивление источника сигнала, входное сопротивление СИ, параметры воздействия при активизации ОИ.
Зависимость от динамических характеристик измеряемой величины
В соответствии со сложившейся классификацией большинство авторов при рассмотрении динамических процессов, связанных с изменениями самой измеряемой величины и переходными режимами в СИ, выделяют два вида погрешностей: статические и динамические. Статическими называют погрешности измерения постоянных величин. Погрешность в динамическом режиме, т. е. при измерении изменяющейся величины, полагают равной сумме статической и собственно динамической погрешности. Таким образом, динамическую погрешность определяют как разность погрешности в динамическом режиме и статической погрешности СИ.
Существуют два принципиально различных вида СИ: аналоговые (измерительные преобразователи, измерительные приборы с электромеханическими измерительными механизмами) и цифровые (АЦП, цифровые измерительные приборы). Аналоговые СИ работают в следящем режиме, поэтому для оценки динамических свойств можно использовать частотные характеристики, все виды переходных функций. Цифровые СИ функционируют в дискретном времени. Относительно момента пуска результат на выходе появляется через некоторый интервал времени, необходимый для реализации процесса сравнения. Величина этого интервала является временем чистого запаздывания между положением на временной оси измеряемого значения и моментом получения результата.
Аналоговые СИ. Моделью любого реального аналогового СИ является так называемая “динамическая система”, связь между координатами которой описывается линейным дифференциальным уравнением с постоянными коэффициентами вида
, (1.1)
где ai, bi – постоянные коэффициенты, x (t), y (t) – входная и выходная переменные, 
– оператор дифференцирования.
Кроме дифференциального уравнения иногда используют передаточную функцию, частотную передаточную функцию. Оценкой динамических свойств таких устройств являются параметры реакции на стандартные входные сигналы: единичный скачок, дельта-функцию, гармоническое воздействие. К ним относятся время нарастания, время установления, амплитуда и фаза выходного сигнала. Для аналоговых СИ воздействия типа 1(t) возникают при скачкообразных изменениях входных сигналов или в режиме коммутации. Переходные функции удобно использовать для оценки динамических свойств СИ, а не динамических погрешностей, так как в реальных объектах измерения нет ограничений на форму кривой изменения физических переменных. Наиболее общей моделью, описывающей меняющееся входное воздействие аналогового СИ, является нестационарный случайный процесс.
Динамическая погрешность СИ, представленного уравнением (1.1), при входном сигнале произвольной формы есть разность
,
где y (t) – решение уравнения (1.1) для конкретного вида x (t).
Известно, что общий интеграл линейного дифференциального уравнения (1.1) равен сумме частного решения неоднородного уравнения и полного решения однородного уравнения. Частное решение неоднородного дифференциального уравнения есть вынужденная составляющая yв (t) выходного сигнала y (t). Однородное уравнение получается из исходного, если в нем положить правую часть равной нулю. Его решение yс (t) – свободная составляющая y (t). Любое свободное решение можно представить в виде суммы экспоненциальных слагаемых, число которых равно числу корней характеристического уравнения
.
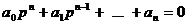Таким образом, значение выхода y (t) =yв (t) +yс (t) при 
стремится к вынужденной составляющей 
(рис. 1.3,а).
а б
Рис. 1.3. Динамическая погрешность
аналогового СИ
Цифровые СИ. Для цифровых СИ не существует промежуточных значений выхода между моментом запуска и получением результата, поэтому основной характеристикой динамических свойств является время измерения τи. При изменяющемся входном сигнале x (t) возникает динамическая погрешность, так как за время от момента пуска t 0 до момента окончания процесса сравнения t 0 + τu входная величина успе-вает измениться от значения x (t 0) до x (t 0 +τu) (рис. 1.4).
На выходе СИ появляется результат 
, и динамическая погрешность равна 
, если статической погрешностью пренебречь. Оценим величину этой погрешности для входного сигнала произвольной формы.
Предположим, что функция x (t) является непрерывной и дифференцируемой на интервале наблюдения. Ее разложение в ряд Тейлора в окрестностях точки t 0 имеет вид
. (1.2)
Продифференцировав ряд (1.2) n раз, выразим коэффициенты полинома через значения производных в точке t 0
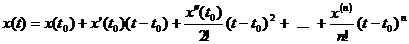. (1.3)
Подставив в разложение (1.2) t = t 0 +τu, найдем динамическую погрешность ∆ (t) как разность x (t 0 +τu)и x (t 0)
. (1.4)
Линеаризовав функцию (1.4) путем отбрасывания всех членов ряда, кроме первого, получим оценку динамической погрешности
.
Таким образом, динамическая погрешность цифровых СИ в первом приближении зависит как от скорости изменения измеряемой физической величины, так и от времени измерения.
Характер проявления при многократных измерениях
Абсолютная погрешность СИ изменяется во времени. Выявить характер этих изменений можно, зафиксировав значение физической величины на входе СИ. Для этого в течение некоторого интервала наблюдения Тн проводят многократные измерения одного и того же заранее известного значения физической величины x 0. Из-за погрешности результаты измерения 
отличаются от истинного значения и группируются около x 0 некоторым образом. Полученный в результате n измерений статистический ряд { 
} графически можно представить в виде совокупности прямоугольников — гистограммы [3]. Основанием каждого прямоугольника служит интервал (xi, xi+ 1) на оси истинных значений x, в котором заключены результаты измерения. Высотой каждого прямоугольника является отношение числа измерений mi, попавших в этот интервал, к общему числу измерений n. При увеличении числа измерений 
и уменьшении ширины интервала ((xi, xi+ 1) 
) гистограмма будет приближаться к кривой, представляющей собой график плотности распределения f (
).На практике для аппроксимации законов распределения используют стандартные функции: нормальную, треугольную, равномерную и др. Оценки параметров функции плотности распределения и являются характеристиками случайной величины , а следовательно, и погрешности ∆i. Если среднее арифметическое 
ряда { } стремится к x 0, погрешность является некоррелированной случайной величиной и ее отдельные выборки ∆ i статистически независимы. Наличие разности – x 0 свидетельствует, что присутствует постоянная составляющая, называемая систематической погрешностью θ. Эта составляющая погрешности остается постоянной или изменяется при измерениях, проводимых на различных интервалах наблюдения. Наличие тенденции в изменении θ говорит о ее корреляции с факторами внешней среды.
Формирование погрешности.
Погрешность данных на выходе канала сбора и обработки измерительной информации формируется в результате суммирования погрешностей преобразования, квантования, цифровой обработки и их трансформации на промежуточных этапах (рис. 1.5).
Значение погрешности и характер ее изменения во времени определяются воздействием суммы множества факторов на измерительный канал. Основными из них являются неинформативные величины: температура окружающей среды, влажность, атмосферное давление, напряжение питания. Изменения этих величин вызывают отклонение электрических режимов измерительного канала из-за
 |
Рис. 1.5. Схема формирования погрешности в измерительном канале
наличия связи параметров элементов схем с этими величинами. Кроме того, протекают процессы деградации, приводящие к изменению параметров элементов. Еще одним источником погрешности является обратное воздействие на значение измеряемой величины x параметров средства измерения. Механизм такого влияния поясним на примере измерения напряжения (рис. 1.6). 
Объект измерения представлен моделью в виде эквивалентного генератора относительно зажимов сопротивления Rн, напряжение на котором необходимо измерить:
,
где Е – напряжение холостого хода (при отключенном Rн); Rвн – внутреннее сопротивление эквивалентного генератора; Rн – сопротивление, на котором измеряется напряжение. Входное сопротивление измерителя подключается параллельно Rн,вызывая увеличение суммарного тока I 0. Падение напряжения на Rвн увеличивается, соответственно на эту же величину уменьшается напряжение на входе СИ.
Абсолютная погрешность определяется по формуле
,
где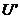 
– напряжение на входе СИ после его подключения к объекту измерения. 
Таким образом, потребляя некоторую мощность от объекта, СИ оказывает на него влияние, изменяя величину информативного параметра U. Возможна ситуация, когда в процессе взаимодействия мощность передается от СИ к ОИ, как, например, при измерении температуры (рис. 1.7). Термодатчик Rt, расположенный на объекте, включен в плечо моста. Его температура tд при выключенном напряжении питания мостового преобразователя равна температуре объекта t 1. После включения питания на датчике начнет рассеиваться мощность от протекающего измерительного тока P=U I, через некоторое время температура датчика возрастет и стабилизируется на некотором уровне t 2. Соответственно изменится сопротивление датчика, а следовательно, и выходное напряжение преобразователя Uвых, тогда при условии R 1 = R 2 = R 3 = R 0 абсолютная погрешность преобразования будет равна
,
где R 0 – сопротивление плеч моста при температуре равновесия моста t 0; ∆R (t 1), ∆R (t 2) – отклонение сопротивления датчика от R 0 при температуре t 1 и t 2 соответственно; Un – напряжение питания моста. Эта погрешность присутствует всегда, несмотря на попытки уменьшить ее путем снижения значения тока I или использования импульсного питания моста.
На погрешность результата измерения оказывают влияние паразитные параметры: сопротивления и емкости соединительных проводов, подключаемых к ОИ, переходные сопротивления контактов в подcтыковочных устройствах, сопротивления контактов коммутаторов в автоматических средствах измерения. Эти сопротивления суммируются либо с входными параметрами 
измерительного устройства, либо с измеряемыми величинами. Так, при измерении малых сопротивлений переходные сопротивления контактов rк и сопротивления подводящих проводов rп включаются последовательно с измеряемым сопротивлением Rx (рис. 1.8).
Относительная погрешность измерения
.
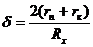Ряд методических погрешностей появляется из-за упрощений и ограничений, накладываемых на используемую модель объекта измерения. Ее неадекватность реальному физическому объекту требует дополнительного уточнения условий измерения.
Цифровое представление физической величины N(x)= 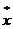является результатом процесса аналого-цифрового преобразования и сопровождается методическими и инструментальными погрешностями. Методические погрешности связаны с дискретизацией величины x(t) во времени и её квантованием по уровню. Дискретизация во времени при аналого-цифровом преобразовании принципиально неизбежна, так как цифровое представление существует в дискретные моменты времени. Погрешность квантования определяется числом разрядов АЦП и по абсолютной величине не превышает ступени квантования.
Для анализа процесса преобразования непрерывной величины в дискретную на выходе аналоговой части измерительного канала воспользуемся ее представлением в виде бесконечного ряда. Учитывая, что средства аналого-цифрового преобразования используют двоичное кодирование, обозначим аналоговую величину A на входе АЦП (напряжение, частоту, временной интервал, сопротивление) как сумму двоичного ряда 
, где bi=0, 1. Как и любой промежуточный результат в измерительном канале, аналоговая величина A содержит информативную составляющую, соответствующую истинному значению физической величины x, и погрешность ∆. Каждую составляющую можно также представить бесконечным двоичным рядом
, (1.5)
. (1.6)
Если учитывать только погрешность квантования, процесс преобразования есть отбрасывание членов ряда начиная с n - го. Результат на выходе АЦП — двоичное число, значащие цифры которого совпадают с bi:
, (1.7)