II. Оценка качества модели

Основная информация для анализа качества любой модели содержится в ряде остатков .

Анализ качества заключается в оценке адекватности модели и оценке уровня её точности.

Адекватность – это соответствие модели определённым статистическим свойствам:

а) свойство случайности уровней в ряде остатков;

б) свойство независимости уровней в ряде остатков или отсутствие автокорреляции (корреляция внутри ряда);

в) соответствие ряда остатков нормальному закону распределения.

Точность модели – это отклонение фактических данных показателя и его расчётных значений в среднем по всей длине временного ряда.

Пример (продолжение):

2) Для проверки качества модели подготовим расчетную таблицу:

		Точки поворота						отн.
	-3,2	-	10,24	-1	-2,2	4,84		12,8%
	-1			2,2	-3,2	10,24		3,3%
	2,2		4,84	4,4	-2,2	4,84		6,1%
	4,4		19,36	-1,4	5,8	33,64		10,7%
	-1,4		1,96	0,8	-2,2	4,84		3,7%
	0,8		0,64		-1,2	1,44		4,9%
				-2,8	4,8			4,3%
	-2,8		7,84	-0,6	-2,2	4,84		6,2%
	-0,6	-	0,36	-	-	-	-	1,2%
		р=4	50,24	-	-	87,72		50,2%

1. Проверка адекватности

а) Свойство случайности уровней в ряде остатков проверяется на основе критерия поворотных точек или критерия пиков

Уровень в ряде остатков называется поворотной точкой (пиком), если он одновременно больше или одновременно меньше двух соседних с ним уровней. Поворотным точкам присваивают значение 1, остальным уровням – 0.

Свойство случайности выполняется, если количество поворотных точек p удовлетворяет неравенству

,

где n-число уровней во временном ряду. Квадратные скобки означают, что от числа, полученного внутри них, нужно взять целую часть.

Так, для нашего примера, т.е. для n=9, в квадратных скобках получим . Т.к. p=4>2, то уровни в ряде остатков, который дала наша модель, являются случайными значениями.

Замечание: количество поворотных точек p=4 можно определить, построив график ряда остатков

б) свойство независимости уровней в ряде остатков или отсутствие автокорреляции между его уровнями проверяется по d-критерию Дарбина-Уотсона

Значение d-критерия рассчитывают по формуле:

Для этого критерия задаются две табличные границы и . В зависимости от попадания d в один из 4-х возможных промежутков делают один из следующих выводов:

- – в ряде остатков присутствует автокорреляция, т.е. свойство независимости остатков не выполняется;

- – d-критерий не подходит для анализа независимости остатков.

В этом случае нужно использовать другой критерий, например, первый коэффициент автокорреляции r(1):

.

Если 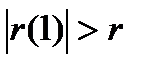, где r – табличное значение, то в ряде остатков присутствует автокорреляция.

- – свойство независимости выполняется, автокорреляция отсутствует.

- – значение d корректируют и находят . Вывод о наличии автокорреляции делают в зависимости от попадания 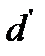в один из уже рассмотренных промежутков.

Проверим d-критерий для нашего примера. В качестве табличных значений используем 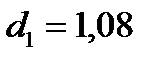и .

,

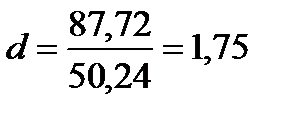
следовательно свойство независимости выполняется, автокорреляция остатков отсутствует.

в) Проверка свойства нормальности распределения ряда остатка осуществляется на основе RS-критерия:

RS=

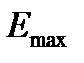– это наибольшее значение уровней в ряде остатков,

– это наименьшее значение уровней в ряде остатков,

S – среднеквадратическое отклонение ряда остатков:

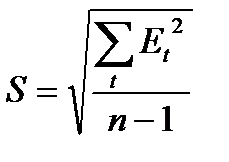
n – кол-во уровней ряда.

Если RS принадлежит табличному промежутку, то ряд остатков распределен по нормальному закону.

В нашем примере

,

RS=(4,4-(-3,2))/2,5=7,6/2,5=3. Принадлежит табличному промежутку (2,7;3,7), следовательно, ряд остатков распределен по нормальному закону.

Вывод об адекватности: все статистические свойства для ряда остатков нашей модели выполнены, следовательно, построенная модель является адекватной.

2. Оценка уровня точности модели

Для проверки точности можно использовать среднюю квадратическую ошибку (СКО) S или среднюю относительную ошибку. Последняя определяется по формулам

,

.

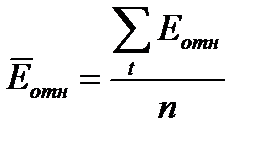Если 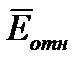< 5%, то уровень точности модели можно считать удовлетворительным. показывает, на сколько процентов в среднем фактические данные отличаются от расчётных значений, полученных по модели.

В нашем примере

и т.д.

Так как 5,58%>5, то уровень точности модели недостаточный. Фактические данные показателя отличаются от расчётных в среднем на 5,58%.

Общий вывод о качестве модели : качественные характеристики модели недостаточны для использования для прогнозирования.