Контрольные вопросы
1. Какая случайная величина называется непрерывной?
2. Что называется функцией распределения?
3. Что называется плотностью вероятности?
4. Какова связь между функцией распределения и плотностью вероятности?
5. Приведите формулы для вычисления математического ожидания и дисперсии непрерывной случайной величины.
26. Дана функция распределения (закон Коши):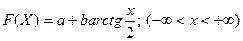 
. Найти параметры а и b, плотность вероятности и вероятность 
.
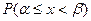Ответ: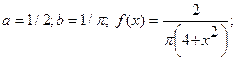 
.
27. Случайная величина Х распределена по закону «прямоугольного треугольника» в интервале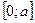 
. Написать выражение плотности распределения. Найти вероятность того, что значение случайной величины оказалось на интервале 
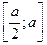. Найти числовые характеристики случайной величины.
Ответ: 
28. Шкала секундомера имеет цену деления 0,2 с.Какова вероятность сделать отсчёт времени с ошибкой более ±0.05 с., если отсчёт делается с округлением до ближайшего деления?
Ответ:0,5
29.Плотность вероятности случайной величины Х, подчиненной закону арксинуса, имеет вид 
. Определить дисперсию. Ответ: 
30. Скорость молекулы газа распределена по закону Максвелла с плотностью вероятности 
Найти математическое ожидание скорости и значение А при заданном 
.
Ответ: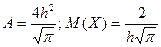 
З А Д А Н И Е 7
Нормальный закон распределения и системы случайных величин
Контрольные вопросы
1. Что такое нормальный закон распределения?
2. Чем вызван почти универсальный характер нормального распределения?
3. Что такое коэффициент корреляции? Что он характеризует?
4. Какова связь между некоррелированностью и независимостью?
31.Случайная величина Х распределена нормально с параметрами 
=10 и s=2. Найти вероятность того, что значение случайной величины Х попадет в интервал (-5: 15)
Ответ: 1,00
32.Случайная величина Х распределена нормально с параметрами =10 и s=5. Найти интервал, в который с вероятностью 0,9973 попадет значение Х в результате опыта.
Ответ: (-5; 25).
33.Деталь, изготовленная автоматом, считается годной, если отклонение ее контрольного размера от проектного не превышает 10 мм. Случайные отклонения контролируемого размера от проектного подчинены нормальному закону со средним квадратичным отклонением 
мм и математическим ожиданием а =0. Сколько процентов годных изделий изготавливает автомат? Ответ: 95,4%.
34.Бомбардировщик пролетает вдоль места длиною 30 и шириною 8 м. Случайные величины Х и У – расстояние от места разрыва бомбы до осей симметрии моста – независимы и подчинены нормальному закону распределения с математическими ожиданиями, равными нулю и средними квадратическими отклонениями, равными соответственно 6 и 4 м. Найти вероятность попадания при одной сброшенной бомбе и вероятность хотя бы одного попадания при двух бомбах.
Ответ: 0,674; 0,894.
35. Дана система двух случайных величин. Найти условные математические ожидания и дисперсии, безусловные математические ожидания и дисперсии и коэффициент корреляции. Сделать вывод о тесноте связи между величинами Х и Y.
М(х)=5.39, М(у)=68,35,D(x)=11.44, D(y)=5157, r=0,87