Система трёх линейных уравнений с тремя неизвестными

Матрицы

Матрицей размера т ´ п называется прямоугольная таблица чисел, содержащая т строк и п столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С,..., а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: а_ij, где i — номер строки, j — номер столбца.

 

 

Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. а_ij=b_ij,для любых

 

Задание 1. Выяснить равны ли матрицы А и В:

вывод:	вывод:
вывод:	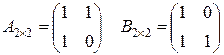вывод:

 

Матрица, состоящая из одной строки, называет­ся матрицей-строкой (вектором-строкой), а из одного столбца — матри­цей-столбцом (вектором-столбцом).

 

Задание 2. Из предложенных матриц найти матрицу-строку и матрицу-столбец:

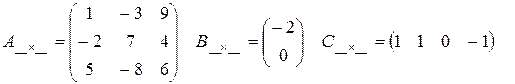
Матрица называется квадратной n -го порядка, если число её строк равно числу столбцов и равно n.

 

Задание 3. Придумайте и запишите квадратные матрицы:

Квадратная матрица первого порядка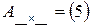
Квадратная матрица второго порядка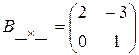
Квадратная матрица третьего порядка
Квадратная матрица четвёртого порядка

 

Элементы матрицы a_tj, у которых номер столбца равен номеру строки (i = j), называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы а_{11 ,} а_{22 , …,} а_nn.

 

Задание 4. Подчеркните диагональные элементы каждой матрицы:

 

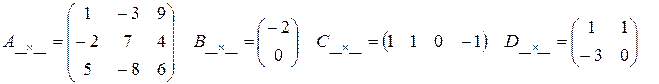
Если все недиагональные элементы квадратной матрицы рав­ны нулю, то матрица называется диагональной.

Задание 5. Укажите диагональные матрицы:

диагональные матрицы:

диагональные матрицы:

 

Квадратная матрица называется треугольной, если все её элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Задание 6. Укажите треугольные матрицы:

треугольные матрицы:

треугольные матрицы:

Если у диагональной матрицы n -го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n -ro порядка – Е.

Задание 7. Укажите единичные матрицы:

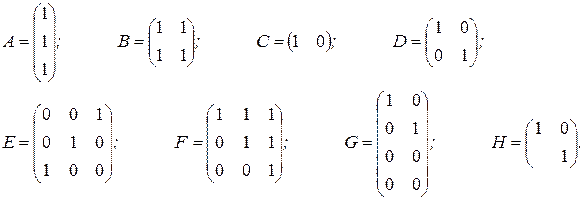единичные матрицы:

единичные матрицы:

 

Матрица любого размера называется нулевой, или нуль-матрицей, если все её элементы равны нулю – О.

В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике.

Матрица размера 1´1, состоящая из одного числа, отождествляется с этим числом, т.е. (5)_1´1=5.

Задание 8. Укажите нулевые матрицы:

нулевые матрицы:

 

Действия над матрицами

Умножение матрицы на число: Произведением матрицы А на число l называется матрица В=Аl, элементы которой b_ij=а_ijl, для

Общий множитель всех элементов матрицы можно выносить за знак матрицы.

 

Задание 9. Выполните действия:

Вычислить:	Вынести общий множитель:
Вычислить:	Вынести общий множитель:
Вычислить:	Вынести общий множитель:

Операции сложения и вычитания матриц выполняются только для матриц одинаковых размеров (порядков):

 

Сложение матриц: Суммой двух матриц А и В одинакового размера т ´ п называется матрица С= А+В, элементы кото­рой с_ij=а_ij+b_ij,для (т.е. матрицы складываются поэлементно).

Вычитание матриц: Разность двух матриц одинакового раз­мера определяется через предыдущие операции: А-В=А+ (-1)· В.

 

Задание 10. Вычислите сумму и разность матриц (если возможно):

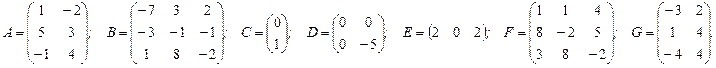
Операция умножения выполняется только для матриц, у которых число столбцов первой матрицы равно числу строк второй.

Умножение матриц: Произведением матриц А_{т ´ k}·В_{k ´ п} называется такая матрица С_{т ´ n}, каждый элемент которой с_ij, равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы j -го столбца матрицы В.

 

Задание 11. Вычислите произведение матриц (если возможно):

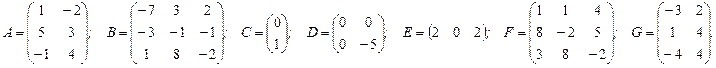
Транспонирование матрицы: переход от матрицы А к мат­рице А¢ (А ^т), в которой строки и столбцы поменялись местами с со­хранением порядка. Матрица А¢ (А ^т)называется транспонированной относительно матрицы А.

 

Задание 12. Найти матрицы, транспонированные данным:

Деление матриц: Деление матрицы А на матрицу В определяется следующим образом через умножение: А: В = А · В ^-1, где В ^-1 – обратная матрица для В.

Итак, деление матрицы А на матрицу В возможно при соблюдении вообще говоря двух условий:

1) матрица В ^-1 – обратная матрица для В должна существовать (В – невырожденная, квадратная n -го порядка);

2) число столбцов матрицы А равно n.

Определители

Определитель — число, характеризующее квадратную матрицу А, обозначается | А | или detA или D.

1) Определителем матрицы первого порядка А =(а), или определителем первого порядка, называется элемент а:

D=| А |=| а |= а.

2) Определителем матрицы второго порядка , или определителем второго порядка, называется число, которое определяется по формуле:

3) Определителем матрицы третьего порядка , или определителем третьего порядка, называется число, которое определяется по формуле:

 

Для вычисления определителя третьего порядка пользуются правилами треугольника и параллелограмма.

Правило треугольника:

 

·	·	·			·	·	·		·	·	·
·	·	·	=	+	·	·	·	-	·	·	·
·	·	·			·	·	·		·	·	·

 

Правило параллелограмма:

 

·	·	·		+	·	·	·	-	1 строка
·	·	·	=	+	·	·	·	-	2 строка
·	·	·		+	·	·	·	-	3 строка
					·	·	·		1 строка
					·	·	·		2 строка

 

Задание 13. Вычислить определители:

Вычислить определитель первого порядка:
Вычислить определитель второго порядка:
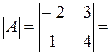
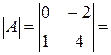
Вычислить определитель третьего порядка по правилу треугольника:
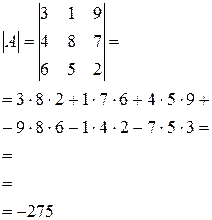
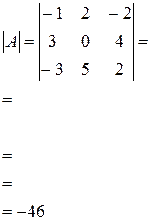
Вычислить определитель третьего порядка по правилу параллелограмма:

Минором М_ij элемента a_ij матрицы n -го порядка называется определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i -й строки и j-ro столбца.

Каждая матрица n -го порядка имеет п² миноров (n -1)-го по­рядка.

 

Задание 14. Вычислить все миноры заданной матрицы:

 

Алгебраическим дополнением А_ij элемента a_ij матрицы п -го порядка называется его минор, взятый со знаком (-1) ^{i + j}:

А_ij =(-1) ^{i + j} · М_ij

 

Задание 15. Вычислить все алгебраические дополнения заданной матрицы:

 

Теорема Лапласа: Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгеб­раические дополнения:

- разложение по элементам i -й строки;

- разложение по элементам j -го столбца.

Вычислите определитель:

Вычислим определитель четвёртого порядка путём его разложения по элементам, например, первого столбца, для чего методом Гаусса приведём его к следующему виду:

Где определитель третьего порядка вычислен по формуле:

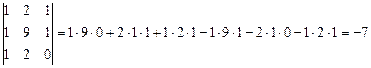
Итак, получили:

Обратная матрица

Матрица А^-1 называется обратной по отноше­нию к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:

А·А^-1=А^-1·А=Е.

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.

Однако не каждая квадратная матрица имеет обратную. Для существования матрицы А^-1 необходимым и достаточным усло­вием является требование | А |¹0.

Ищем А ^-1 – обратную матрицу для А (если она существует) по формуле:

Система трёх линейных уравнений с тремя неизвестными

Систему линейных алгебраических уравнений решить тремя способами:

1. методом Гаусса;

2. по формулам Крамера;