Семинар 6.
Тема: Технология MPI: параллельная реализация циклов
План:
· Введение – какие функции MPI мы знаем
· Параллельная реализация циклов. Пояснения и примеры.
· Задания
Введение
На предыдущих семинарах мы освоили 12 необходимых и\или наиболее популярных функций технологии MPI. Хотя библиотека MPI содержит более 200 функций - полученных знаний вполне достаточно, чтобы составлять программы для эффективного выполнения задач в параллельном режиме. Итак, что мы знаем:
Функции общего назначения (4 штуки)
MPI_Init – инициализация работы с MPI
MPI_Finalize – завершение работы с MPI
MPI_Comm_rank – определение номера процесса
MPI_Comm_size – определение размера группы (количества процессов в группе)
Функции для организации обмена между отдельными процессами
MPI_Send – блокирующая отправка данных процессу с заданным номером
MPI_Recv – блокирующий прием данных от процесса с заданным номером
MPI_Isend – неблокирующая отправка данных процессу с заданным номером
MPI_Irecv – неблокирующий прием данных от процесса с заданным номером
MPI_Test – вспомогательная функция для проверки завершения неблокироющего приема или передачи
MPI_Wait – вспомогательная функция, обеспечивающая ожидание завершения приема или передачи
MPI_Bcast – широковещательная рассылка данных всем процессам в группе
MPI_Reduce (MPI_Allreduce) – глобальные операции над данными из разных процессов
Организация распределенного выполнения циклов в MPI-программах
Вопрос параллельной реализации циклов затрагивался на Семинаре 2. Остановимся сейчас на этом более подробно.
Наша задача – научиться писать программу в стиле SPMD (single program – multiple data), когда каждый процесс выполняет один и тот же фрагмент кода, обрабатывая при этом по единой схеме свои, назначенные ему данные.
При этом работа между параллельными процессами должна быть распределена так, чтобы: (1) в совокупности работа должна быть выполнена полностью; (2) работы, назначенные к выполнению каждому процессу - не должны «перекрываться».
Рассмотрим задачу поэлементного суммирования двух массивов. Пусть определены значения элементов целочисленных массивов длины N: a[N] и b[N]. Тогда «классический» цикл по сложению элементов этих массивов с сохранением результата в массив с имеет вид:
for(i=0;i<N;i++)
c[i] = a[i]+b[i];
Рассмотрим варианты распределенного вычисления этого цикла. Основных вариантов два – «блочный» и «циклический», а также возможны различные варианты их комбинации.
«Блочное» распределение цикла.
Каждому процессу назначается к расчету фрагмент (блок) элементов массива с длины delta, начинающийся с позиции imin (значение imin – свое в каждом процессе). Размер блока delta вычисляется как delta = N/np. Если длина масссива N делится нацело на количество процессов np – работа между процессами c rank распределена поровну:
int delta = N/np;
imin = rank*delta;
imax = imin+delta;
for(i=imin;i<imax;i++)
c[i] = a[i]+b[i];
Если же N делится на np с остатком – необходимо учесть это при распределении расчета, чтобы все элементы массива с были посчитаны. Один иp вариантов – «назначить» расчет остающейся порции элементов процессу с номером np-1, как показано на схеме:
| Исходный массив | ||||||||||||||
| delta | ||||||||||||||
| delta | ||||||||||||||
| delta | ||||||||||||||
| np-1 | … | delta+ost | ||||||||||||
Учет остатка можно реализовать явным образом:
int ost = N%np;
imin = rank*delta;
imax = imin+delta;
if(rank==np-1) imax += ost;
for(i=imin;i<imax;i++)
c[i] = a[i]+b[i];
либо просто указать, что процесс с номером np-1 вычисляет элементы массива с, начиная с imin до последнего элемента массива, т.е. до N-1 включительно.
imin = rank*delta;
imax = imin+delta;
if(rank== np-1) imax = N;
for(i=imin;i<imax;i++)
c[i] = a[i]+b[i];
В результате выполнения любого из вышеприведенных трех фрагментов каждый процесс будет иметь в своей локальной памяти, в массиве с[N], блок рассчитанных элементов, в то время как остальные значения этого массива не определены. Для «сборки» блоков, посчитанных каждым процессом в единый массив в каком-либо одном назначенном процессе, можно использовать функции пересылки типа «точка – точка» либо функции коллективного взаимодействия типа MPI_Gather. В случае не слишком большой длины массивов сборку блоков в один процесс можно организовать с помощью уже известной нам процедуры MPI_Reduce.
В самом деле, если мы заранее положим все элементы массива с[N] равными 0 в каждом процессе, то получим после выполнения нашего распределенного цикла в каждом процессе массив с[N], в котором только рассчитанный блок содержит полезные данные, а остальные элементы равны 0. Так, для случая N=12, np=4 имеем:
rank=0:
| с[0] | с[1] | с[2] |
rank=1:
| с[3] | с[4] | с[5] |
rank=2:
| с[6] | с[7] | с[8] |
rank=3:
| с[9] | с[10] | с[11] |
Применяя глjбальное суммирование элементов массива из разных процессов c помощью процедуры MPI_Reduce, получим результирующий массив (обозначим его d[N]), содержащий результаты суммирования элементов массива а[N] и массива b[N].
На скриншоте показана программы, в которой объявляются массивы a[N], b[N], c[N], d[N]; с помощью «классического» цикла каждый процесс идентично определяет значения элементов массивов a[N], b[N], c[N]; затем выполняется распределенный цикл, в котором каждый процесс вычисляет свой фрагмент массива с[N]. Далее осуществляются сборка результатов в массив d[N] в процесс с номером 0.
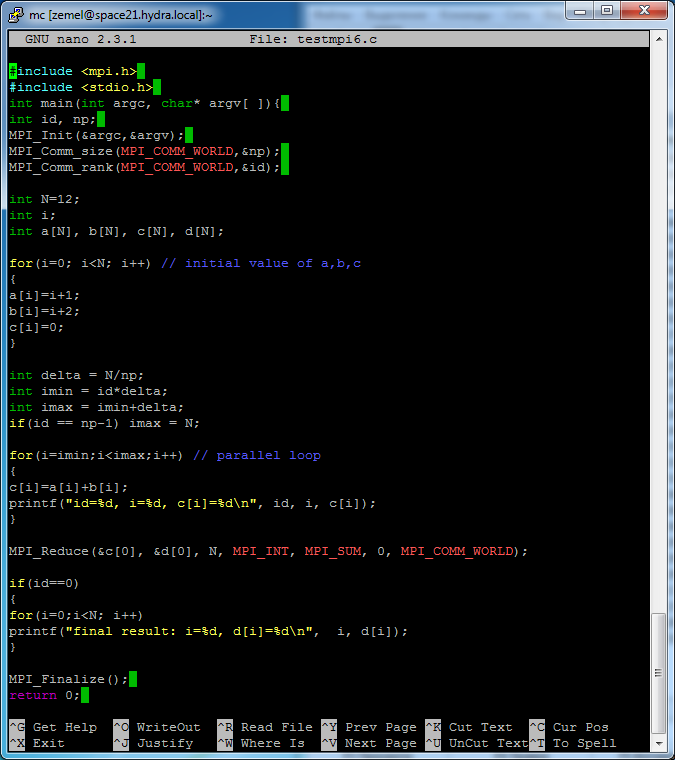
Примечание. Здесь для обозначения номера процесса используется id, а не rank, как в тексте.
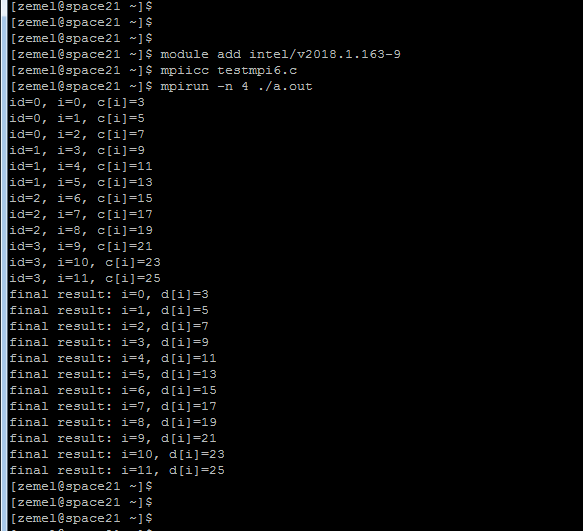
Следующий скриншот показывает результат запуска данной программы для N=12, np=4.
Каждый процесс печатает вычисленные им элементы массива с, затем 0-процесс печатает окончательный результат – массив d[N].
«Циклическое» распределение выполнения цикла.
Другой вариант распределения расчета – циклическое (или итеративное) распределение, заключается в том, что каждый процесс обрабатывает итерации цикла, начиная со своего порядкового номера с шагом, равным числу процессов в группе:
| Исходный массив | ||||||||||||||
| np-1 | ||||||||||||||
Реализация такого распределения на вышеприведенном примере имеет следующий вид:
for(i=rank;i<N;i+=np)
с[i]=a[i]+b[i];
В этом подходе операции по расчету delta, imin, imax – не нужны.
В результате выполнения этого цикла для N=12 и np=4 получаем следующую структуру массивов с[N] в каждом процессе.
rank=0:
| с[0] | с[4] | с[8] |
rank=1:
| с[1] | с[5] | с[9] |
rank=2:
| с[2] | с[6] | с[10] |
rank=3:
| с[3] | с[7] | с[11] |
Понятно, что применение процедуры MPI_Reduce также приведет к правильному формированию результирующего массива d[N].
Задания:
1. Изучить в учебном пособии по MPI раздел 2.3 по параллеьной реализации цикла.
2. Воспроизвести и запустить на кластере HybriLIT рассмотренный пример по блочному распределению поэлементного суммирования двух массивов.
3. Модифицировать рассмотренную программу для случая «циклического» распараллеливания.
4. Модифицировать программу так, чтобы значения массивов a,b,c задавались в процессе с номером 0, а затем производилась рассылка с помощью процедуры MPI_Bcast.