Составить систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях

Анализ электрического состояния линейных и нелинейных электрических цепей постоянного тока

Расчет линейных электрических цепей постоянного тока

Для электрической цепи, изображенной на (рис.1.1), выполнить следующее:

1) составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;

2) определить токи во всех ветвях схемы, используя метод контурных токов;

3) определить токи во всех ветвях схемы на основании метода наложения;

4) составить баланс мощностей для заданной схемы;

5) результаты расчета токов по пунктам 2 и 3 представить в виде таблицы и сравнить;

6) определить ток во второй ветви методом эквивалентного генератора;

7) построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.

Дано: E₁ =65 В, E₂ =15 В, R₁ =53 Ом, R₂ =34 Ом, R₃ =24 Ом, R₄ =18 Ом, R₅ =25 Ом, R₆ =42 Ом, r₀₁ =1 Ом, r₀₂ =1 Ом.

Определить: I_1, I_2, I_3, I_4, I₅, I₆

 

Рисунок 1.1 Исходная схема

Составить систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях

Произвольно задаемся направлением токов в ветвях цепи I₁, I₂, I₃, I₄, I₅, I₆.

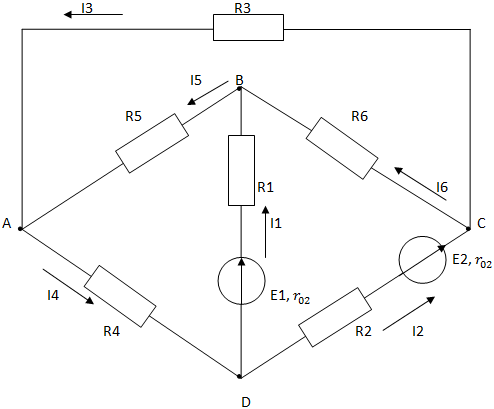
Рисунок 1.2 Схема цепи для составления уравнений по законам Кирхгофа

Составляем систему уравнений (в системе должно быть столько уравнений, сколько в цепи ветвей). В нашей цепи шесть ветвей, значит, в системе будет шесть уравнений. Сначала составляем уравнение по первому закону Кирхгофа. В цепи с n узлами будет (n-1) уравнений, в нашей цепи четыре узла, значит, будет три уравнения. Составляем три уравнения, для трех произвольных узлов.

Узел A: I₅ - I₄ + I₃ = 0

Узел C: I₂ - I₆ - I₃ = 0

Узел B: I₆ - I₅ + I₁= 0

Теперь составляем недостающие три уравнения для трех независимых контуров. Чтобы они были независимыми, надо в каждый контур включить хотя бы одну ветвь, не входящую в предыдущую.

Задаемся обходам каждого контура и составляем уравнения по второму закону Кирхгофа.

Контур CD- обход против часовой стрелки

E₁ =I₁ (R₁ +r₀₁) + I₅R₅+ I₄R₄

Контур AB- обход против часовой стрелки

E₂ – E₁ = I₂ (R₂ +r₀₂) + I₆R₆ - I₁ (R₁ +r₀₁)

Контур ACDB- обход против часовой стрелки

0 = I₃R₃ – I₅R₅ – I₆R₆

ЭДС в контуре берется со знаком "+", если направление ЭДС совпадает с обходом контура, если не совпадает - знак "-".

Падения напряжения на сопротивления контура, берется со знаком "+", если направления тока в нем совпадает с обходом контура со знаком "-", если не совпадает.

Мы получили систему из шести уравнений с шестью неизвестными:

Решив систему, определим величину и направление тока во всех ветвях схемы.

Если при решении системы ток получается со знаком "-", значит его действительное направление обратно тому направлению, которым мы задались.

2) Определить токи во всех ветвях схемы, используя метод контурных токов

 

Рисунок 1.3 Схема цепи для вычисления методом контурных токов

В заданной цепи можно рассмотреть три контура-ячейки и вести для них контурные токи I₁₁, I₂₂, I₃₃.

Контуры-ячейки имеют ветвь, не входящую в другие контуры - это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей.

Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.

При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.

На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим:

Стрелками указываем выбранные направления контурных токов I₁₁, I₂₂, I₃₃ в контурах-ячейках (направление обхода контуров принимаем таким же);

Составляем уравнения и решаем систему уравнений или методом подстановки, или с помощью определителей.

Подставляем численное значение ЭДС и сопротивлений:

 

Решим систему с помощью определителей. Вычислим определитель системы Δ и частные определители Δ₁, Δ₂, Δ_3.

 

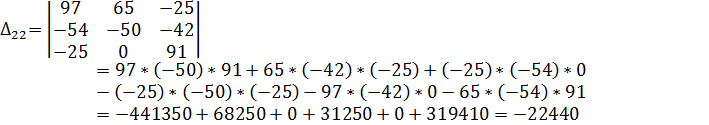
Вычислим контурные токи:

Вычислим действительные токи: