Теоретическое введение
Упорядоченное движение электрических зарядов под действием сил электрического поля называется электрическим током проводника. Необходимыми условиями существования тока являются: 1) наличие свободных зарядов; 2) наличие разности потенциалов на концах проводника. За направление тока принято направление движения положительных зарядов. Электрический ток характеризуется силой тока. Сила тока численно равна заряду проходящему через поперечное сечение проводника за единицу времени. Если за бесконечно малый промежуток времени dt через поперечное сечение проводника проходит заряд dq, то мгновенная сила тока I=dq/dt. Для постоянного тока его величина определяется соотношением I=q/t, где q-заряд, прошедший через поперечное сечение проводника за время t. За единицу силы тока принимается 1Ампер (А). При силе тока в 1А через поперечное сечение проводника протекает заряд 1Кулон.
Электрический ток характеризуется также плотностью тока j=dI/dSn, где dI- ток через физически бесконечно малую площадку dSn, перпендикулярную направлению тока. Ток, величина и направление которого не изменяется со временем, называется постоянным током. Если величина и направление тока изменяются со временем, то ток называется переменным. При наличии электрического тока напряженность электрического поля 
внутри проводника не равна нулю, а силовые линии вектора Е не перпендикулярны поверхности проводника. При этом поверхность проводника не является эквипотенциальной.
Рассмотрим участок проводника не имеющий разветвлений (рис.10.1).
Рис. 10.1
Участок ограничен сечениями 1 и 2 с потенциалами j1 и j2. Величина напряжения на этом участке U=j1-j2. Работа А по перемещению заряда q под действием сил электрического поля определяется соотношением
A=q(j1-j2) =qU (10.1)
Напряжение на участке 1-2 определяется работой, которую совершают силы поля над единичным положительным зарядом
U=A/q (10.2)
Напряжение 1вольт (1В) соответствует работе в один джоуль (1Дж) при прохождении через сечение проводника заряда один кулон (1К). Ом экспериментально установил закон, согласно которому отношение напряжения на .концах проводника к силе тока в нем является постоянной величиной.
(10.3)
Величина R, характеризующая данный проводник, называется сопротивлением проводника. За единицу сопротивления принимается 1Ом. В проводнике c сопротивлением 1Ом протекает 1А при разности потенциалов на его концах 1В.Сопротивление проводника R зависит от материала проводника и его геометрических размеров. Для однородного цилиндрического проводника
(10.4)
где r-удельное сопротивление, l- длина проводника, S-площадь поперечного сечения.Удельное сопротивление проводников увеличивается при увеличении температуры приблизительно по линейному закону.
= 
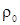(1+at) (10.5)
где 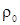-удельное сопротивление при 0 0С, - удельное сопротивление при температуре t 0С, a- постоянная, не зависящая от температуры величина.
При расчете параметров электрических цепей пользуются правилами Кирхгофа:
1.Алгебраическая сумма токов Iк, сходящихся в точке разветвления проводников (узле) равна нулю. Токи, текущие к узлу, считаются положительными, а текущие от узла - отрицательными.
2.В любом замкнутом контуре, выделенном в сложной цепи проводников, алгебраическая сумма падений напряжений Iк Rк на отдельных участках контура (Rк -сопротивление к-го участка) равно алгебраической сумме ЭДС. eк в этом контуре
.
При этом следует считать положительными токи и ЭДС, если направление токов и направление действия ЭДС (направление от отрицательного полюса к положительному) совпадают с направлением обхода по контуру и наоборот.
При последовательном соединении проводников (рис.10.2) R1 и R2 величина тока I в обоих проводниках будет одинакова. Сопротивление рассмотренного участка цепи R
R= 
(10.6)
равно сумме сопротивлений R1 и R2.
Рис. 10.2 Рис. 10.3
При последовательном соединении N проводников их сопротивления складываются
R=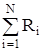 
(10.7)
При параллельном соединении проводников R1 и R2 (рис.10.3) напряжение на проводниках одинаково U = I1R1 = I2R2.
Из закона сохранения заряда следует I = I1 +I2, поэтому
I= 
(10.8)
Для N проводников, соединенных параллельно
(10.9)
Сопротивление проводников можно с высокой степенью точности измерять с помощью моста сопротивлений Уитстона.
Описание лабораторной установки
Принципиальная электрическая схема моста Уитстона изображена на рис.10.4.
В схеме, изображенной на рис.10.4 постоянное напряжение U приложено между точками А и В, R- известное эталонное сопротивление, RX - неизвестное измеряемое сопротивление, Г- гальванометр. Между точками А и В установлена калиброванная проволока - реохорд, имеющая скользящий контакт D. Линейные размеры проволоки между точками A и D - l 1, между точками D и В - l 2. Метод измерения сопротивления с помощью моста Уитстона основан на сравнении неизвестного сопротивления RX с известным сопротивлением R. Пусть токи в плечах моста текут так, как показано на рис.10.4. Тогда по правилам Кирхгофа:
для узла С I - Ix - IГ =0
для узла D I1 + IГ - I2 =0 (10.10)
для контура ACDA IR + IГRГ -I1R1 =0
для контура CBDC IXRX - I2R2 - IГRГ =0
для участка АВ U=I1R1 + I2R2
Рис. 10.4
В выражениях (10.10) RГ - сопротивление гальванометра, R1 и R2 - сопротивления участков реохорда ℓ1 и ℓ2 соответственно. Изменяя положение скользящего контакта D, и тем самым сопротивления R1 и R2, можно добиться того, чтобы потенциал точки D был равен потенциалу точки С (jD =jC). В этом случае ток через гальванометр не течет (мост сбалансирован), IГ = 0. Поэтому из соотношений (10.10) следует:
IX = I, I1 =I2, IXRX = I2R2, IR =I1R1.
(10.11)
Учтя, что IX = I, a I1 = I2 из (10.11) получим
(10.12)
Сопротивления реохорда R1 и R2 определяются выражением (10.4) и поэтому (10.12) можно представить в виде
, R=0,47 Koм (10.13)
В исследуемой лабораторной установке в качестве неизвестных сопротивлений используются три резистора RX1, RX2, RX3, величины которых определяются экспериментально с помощью соотношения (10.13).