Теоретическое введение
Известно, что индуктивность L есть коэффициент пропорциональности между током в проводнике и магнитным потоком, создаваемым этим током.
На примере длинного (ℓ >>r, т.е. длина соленоида много больше радиуса витка) соленоида, можно показать, что L, подобно емкости, зависит от геометрии и формы проводника, а также от магнитной проницаемости сердечника.
Действительно, индукция магнитного поля длинного соленоида
, (15.1)
где m0 - магнитная постоянная (m0 = 4p×10-7 Г/м);
m - магнитная проницаемость сердечника; (в отсутствие ферромагнитного сердечника m=1); N – число витков соленоида; ℓ- длина соленоида; I 
- величина тока, сечение соленоида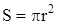 
.
Магнитный поток через соленоид: 
и в отсутствие ферромагнитного сердечника (m=1) можно считать 
= сonst. ЭДС самоиндукции равна:
e 
. (15.2)
При L = const, величина индуктивности зависит лишь от геометрии проводника и может быть рассчитана по формуле
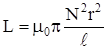. (15.3)
Для 
приближенно:
. (15.4)
В данной работе параметры L-C-R контура могут быть определены двумя способами, а именно: используя режим затухающих колебаний или явление резонанса в режиме вынужденных колебаний. Оба этих способа, коротко описанные ниже, используются при выполнении работы
При подаче импульса напряжения от внешнего ЗГ в колебательном контуре, состоящем из активного сопротивления R, индуктивности L и емкости С, возникают затухающие колебания с частотой w, равной собственной частоте колебательного контура (см. Общие сведения о колебаниях и теор. введение к лаб. работе №13).
Экспериментально определив период затухающих колебаний Т и декремент затухания b в L-C контуре, можно рассчитать индуктивность соленоида при заданной емкости, и, наоборот, поскольку частота затухающих колебаний 
.
Если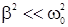 
, то с учетом входной емкости осциллографа С0 индуктивность можно рассчитать по формуле Томпсона (Введение (22)), т.е.
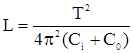. (15.5)
Резонансную частоту можно экспериментально определить в режиме вынужденных колебаний, используя явление резонанса. Обратите внимание, что если первым способом (в режиме затухающих колебаний.), в принципе, возможна оценка каждого из трех основных параметров контура, то при использовании явления резонанса в режиме вынужденных колебаний могут быть оценены только L и C.
Нужно отметить, что в данной работе b2 << w02, т.е. R2/4L2 << 1/LC, поэтому возможно использование формулы Томпсона 
и сравнение результатов, полученных обоими вышеописанными методами.
Описание. Принцип работы лабораторной установки
Схема установки приведена на рис.15.1.
К катушке L0 от генератора прямоугольных импульсов (ЗГ) прикладывается напряжение низкой частоты (50 -100 Гц). Колебания в исследуемом контуре L-C-R возникают за счет индуктивной связи между катушкой L0 и вставленной внутрь нее «исследуемой» катушкой Li. Магнитный поток, создаваемый L0, пронизывает витки Li, создавая в ней переменную ЭДС индукции, частота которой равна частоте генератора nи заведомо ниже собственной частоты контура w0 (w0 >> w = 2pn). В результате в L-C-R контуре возникают собственные затухающие колебания частоты 
(
), величина которой определяется параметрами контура. Сигнал с емкости исследуемого контура подается на вход Y осциллографа (С0 – внутренняя входная емкость осциллографа).
Рис.15.1
Измерения периода свободных затухающих колебаний проводятся при помощи осциллографа так же, как в работе (13). Схематически изображение, возникающее на экране осциллографа, показано на рис.2 (Введение)
При измерениях используются три катушки L3, L6 и L7, к каждой из которых поочередно подсоединяются емкости С1, С2,С3.
Для наблюдения резонанса в контуре необходимо от звукового генератора (ЗГ) подать переменное напряжение с частотой w, примерно равной собственной частоте контура. При совпадении w и wрез, т. е. частоты генератора и резонансной частоты данного L-C-R контура (см. работу № 14), в нем возникнут вынужденные незатухающие колебания и будет наблюдаться явление резонанса, регистрируемое по максимальной амплитуде колебаний на экране осциллографа (величина w=wрез подбирается экспериментально).
Выполнение работы
В настоящей работе предполагается экспериментальное определение описанными способами только одного из параметров L-C-R контура, а именно, L. Используя полученные результаты и данные таб. 15.1, необходимо проанализировать зависимость индуктивности соленоида от числа витков в нем – L(N).
а) Режим затухающих колебаний.
Собрать схему рис.15.1.
Установить на звуковом генераторе частоту 100 Гц (прямоугольные импульсы). Подбирая постоянную развертки осциллографа и коэффициент усиления, получить устойчивое изображение затухающих колебаний в пределах рабочей части экрана осциллографа. При этом ручка ДЛИТЕЛЬНОСТЬ на панели осциллографа должна быть установлена в крайнее правое положение.
В качестве индуктивности подключать катушки L3, L6, L7 с одинаковыми радиусами намотки r = 26 мм. Провести по три измерения для каждой катушки, подключая известные емкости – С1, С2 и С3.
Определить период Т наблюдаемых на экране колебаний по известной длительности развертки: 
.
Здесь t - длительность развертка;
n- количество периодов колебаний:
m- число делений на экране осциллографа, соответствующее этому числу периодов.
Рассчитать значение индуктивностей по ф-ле (15.5).
По результатам трех измерений определить среднее значение каждой из индуктивностей. Все данные занести в таблицу.
Определить период Т наблюдаемых на экране колебаний по известной длительности развертки: .
Здесь t - длительность развертка;
n- количество периодов колебаний:
m- число делений на экране осциллографа, соответствующее этому числу периодов.
Рассчитать значение индуктивностей по ф-ле (15.5).
По результатам трех измерений определить среднее значение каждой из индуктивностей. Все данные занести в таблицу.
б) Явление резонанса в режиме вынужденных колебаний.
Изменяя частоту колебаний генератора, добиться резкого усиления амплитуды колебаний на экране осциллографа, т. е. явления резонанса в контуре.
Подсоединяя поочередно различные емкости и индуктивности, как в предыдущей серии экспериментов, определить значения резонансной частоты для каждого случая. По экспериментально определенным значениям резонансных частот рассчитайте соответствующие им периоды колебаний и далее по формуле (15.5) - индуктивности катушек. Данные занесите в таблицу и сравните с уже полученными результатами.
На основе полученных данных сделать вывод о зависимости индуктивности соленоида от числа витков в нем ‑ L(N).
Контрольные вопросы
1. Что такое индуктивность? Какова ее размерность?
2. Вывести формулу для индуктивности бесконечно длинного соленоида.
3. В чем состоит явление электромагнитной индукции?
4. Как определить период колебаний в колебательном контуре в данной работе?
5. Как зависит индуктивность соленоида от его геометрических размеров?