Описание лабораторной установки. Теоретическое введение

Теоретическое введение

 

Опыт показывает, что электрические токи взаимодействуют между собой. Например, два тонких прямолинейных параллельных проводника, по которым текут токи (их называют прямыми токами), притягиваются друг к другу, если токи в них имеют одинаковое направление, и отталкиваются, если токи противоположны.

Взаимодействие токов осуществляется через поле, которое называют магнитным. Магнитное поле представляет собой вид материи, посредством которой осуществляются взаимодействия движущихся электрических зарядов. Другими словами, всякие движущиеся заряды (электрические токи) возбуждают в окружающем их пространстве магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы. Магнитное поле, в отличие от электрического, не оказывает действия на покоящиеся заряды.

Покоящиеся в данной системе отсчета заряды магнитное поле не создают. Обнаружить магнитное поле можно по его силовому действию на движущиеся заряженные частицы, токи, намагниченные тела (магнитную стрелку).

Для изучения магнитного поля можно взять плоский замкнутый контур с током и поместить его в исследуемую точку поля. Магнитное поле ориентирует такой свободный контур с током (как и магнитную стрелку) определенным образом. Опыт показывает, что максимальное значение момента сил , поворачивающего такой контур с током, пропорционально площади S контура и силе тока I в нем (M~IS).

Величина IS является модулем так называемого магнитного момента P_m контура с током. Сам же магнитный момент P_m представляет собой вектор

(7.1)

где - единичный вектор (нормаль к плоскому контуру), связанный с направлением тока I в контуре (рис.7.1) правилом правого винта (если направление вращения головки винта совпадает с направлением тока I в контуре, то поступательное движение винта укажет направление вектора ).

 

Рис. 7.1

Отношение максимального значения момента сил М, действующего на контур с током в данной точке поля, к его магнитному момент P_m остается постоянным и может быть силовой характеристикой поля, называемой магнитной индукцией В, т.е.

(7.2)

Таким образом, магнитная индукция в некоторой точке поля численно равна максимальному моменту силы, действующему на контур с током с единичным магнитным моментом, помещенным в эту точку поля.

Как показано на рис.7.1, магнитная индукция - вектор, направление которого совпадает с направлением нормали к плоскости контура с током в положении его устойчивого равновесия.

Единицей магнитной индукции в СИ является тесла (Тл). Если поле в данной точке характеризуется магнитной индукцией 1Тл, то на контур, магнитный момент которого 1Ам² действует максимальный момент силы 1Нм.

Для магнитных полей, как и для электрических, справедлив принцип суперпозиции: магнитная индукция поля , создаваемого несколькими токами, равна векторной сумме индукции полей каждого из токов в отдельности,

(7.3)

где N- число токов.

Магнитное поле можно изобразить графически с помощью линий магнитной индукции, касательные к ним показывают направление вектора , а его значение равно числу линий, проходящих через единичную перпендикулярную им площадку. Линии магнитной индукции всегда замкнуты, они не имеют начала и конца - такие поля называют вихревыми.

Направление линий магнитной индукции определяется правилом правого винта (если поступательное движение правого винта совпадает с направлением тока, то направление вращения головки винта укажет направление линий магнитной индукции).

Индукция (при прочих одинаковых условиях) зависит от свойств среды. Индукция В в среде (в веществе) и индукция В₀ в вакууме связаны соотношением

(7.4)

Безразмерная величина m характеризует магнитные свойства и называется магнитной проницаемостью среды. Она показывает, во сколько раз индукция в рассматриваемой точке поля в данном веществе больше, чем в вакууме.

Наряду с индукцией существует и другая характеристика магнитного поля - напряженность , связанная с магнитной индукцией соотношением

В=m₀mH (7.5)

где m₀ - магнитная постоянная, зависящая от выбора единиц.

Таким образом, напряженность магнитного поля есть вектор, в m₀m раз меньший, чем вектор .

Введение вектора связано с трудностью определения индукции в веществе, т.к. последняя зависит от свойств среды. Величина же во многих случаях не зависит от свойств среды и определяется только значениями и расположением токов, создающих магнитное поле. Единица напряженности

Проведенные опыты по изучению магнитных полей проводниками различной формы показали, что:

1)Во всех случаях индукция магнитного поля пропорциональна силе тока I,

2) Магнитная индукция зависит от формы и размеров проводника с током.

3)Магнитная индукция в произвольной точке поля зависит от расположения этой точки по отношению к проводнику с током.

Био, Савар и Лаплас обобщили опыты и получили общий закон, который позволяет вычислить индукцию в каждой точке поля, создаваемого током, текущим по проводникам любой формы

(7.6)

где I -сила тока, -вектор, совпадающий с элементарным участком тока и направленный в сторону, в какую течет ток, его называют элементом тока, 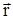-радиус-вектор, проведенный от элемента тока в ту точку, в которой определяется индукция , r-модуль этого вектора. Направление вектора находят по правилу правого винта.

В скалярном виде закон Био-Савара-Лапласа записывают так:

(7.7)

где j -угол между направлением вектора элемента тока и радиусом-вектором .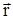

Рис. 7.2.

 

Расчет магнитных полей проводников с током произвольной формы сложен. Однако расчет упрощается, если проводник с током имеет определенную симметрию, например, прямолинейный проводник (рис.7.2). Найдем индукцию магнитного поля в точке А на расстоянии r₀ от проводника с током I. Для этого разобьем проводник на элементы тока (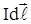). Согласно (7,6) в произвольной точке А векторы d от всех элементов тока имеют одинаковое направление - перпендикулярно плоскости рисунка вверх. Поэтому векторную сумму векторов d можно заменить суммой их модулей, причем

(7.8)

Перейдем к одной переменной в выражении (7.8), выразив r₀ и через угол j.

Из рис.7.2 видно, что и . Подставив эти выражения в выражение (7.8) и интегрируя последнее по всем элементам тока, что эквивалентно интегрированию по j от j₁ до j₂, находим

(7.9)

Для бесконечно длинного проводника (ℓ>>r₀) будем иметь j₁=0, j₂=p. Тогда выражение (7.9), примет вид

Видно, что индукция магнитного поля тем больше, чем больше сила тока течет по проводнику, и чем ближе к проводнику находится точка А.

Иногда для расчета магнитных полей используют теорему о циркуляции вектора индукции , которая для вакуума формулируется так: Циркуляция вектора индукции магнитного поля по произвольному замкнутому контуру равна произведению m₀ на алгебраическую сумму токов, охватываемых этим контуром, т.е.

(7.10)

где N-число токов. Применим теорему о циркуляции вектора для определения магнитного поля внутри соленоида.

Пусть ток I течет по проводнику, намотанному на поверхность цилиндра. Такой обтекаемый током цилиндр называют соленоидом (рис.7.3). Для соленоида необходимо условие, что ℓ>>r, где ℓ-длина соленоида, r -радиус цилиндра, на который намотан проводник. Пусть на единицу длины соленоида приходится п-витков проводника. Если шаг винтовой линии (расстояние между двумя близлежащими витками) достаточно мал, то каждый виток соленоида можно приближенно заменить замкнутым витком. Опыт показывает, что чем длиннее соленоид, тем меньше индукция В снаружи.

Рис. 7.3

Для бесконечно длинного соленоида (ℓ>>r) индукция снаружи вблизи середины соленоида отсутствует вообще, а внутри соленоида линии индукции направлены вдоль его оси (см. рис.7.3).

В качестве произвольного замкнутого контура возьмем прямоугольный контур (см.1.2.3.4). Тогда интеграл (7.10) разобьем на четыре интеграла, т.е.

(7.11)

где I -ток в одном витке соленоида, N -число витков в соленоиде.

Так как магнитное поле вне соленоида практически равно нулю и на участках 2-3 и 4-1 , то выражение (7.11) принимает вид:

(7.12)

Учитывая, что внутри соленоида B=const, то из выражения (7.12) следует, что:

или B=m₀nI (7.13)

где - число витков на единицу длины.

Формулы (7.13) позволяют рассчитывать магнитное поле в соленоиде по известным n, ℓ и I.

Зная индукцию магнитного поля В, можно рассчитать и напряженность Н магнитного поля по формуле (7.5), т.е.

(7.14)

Проводник с током со стороны магнитного поля испытывает действие силы, которую называют Амперовой силой. Ампер установил, что сила DF с которой магнитное поле действует на отрезок длиной Dℓ с током I, выражается так:

, (7.15)

где j -угол между направлением тока I в проводнике и вектором индукции .

Силу Ампера (7.15) можно записать и в векторном виде:

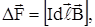
где - вектор, направление которого совпадает с направлением тока в нем.

Вектор всегда перпендикулярен к плоскости в которой лежат вектора и и его направление определяется по правилу правого винта: если головку винта кратчайшим путем повернуть от вектора к вектору , то направление поступательного движения винта укажет направление вектора силы Ампера .

Из действия силы Ампера на проводник с током вытекает, что на точечный заряд q, движущийся в магнитном поле, также действует сила со стороны магнитного поля, ее называют силой Лоренца:

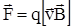или F=qvBsinj (7.16)

где q -заряд, движущийся со скоростью под углом j к направлению вектора индукции .

Сила Лоренца также всегда перпендикулярна плоскости, в которой расположены векторы и , а ее направление определяется правилом правого винта (см. выше), но для случая q< 0 сила будет направлена в противоположную сторону направления поступательного движения винта.

Сила Лоренца действует только на движущийся относительно магнитного поля заряд q. Характерная особенность силы Лоренца состоит в том, что она, будучи всегда перпендикулярной к вектору скорости , играет роль центростремительной силы. Следовательно, сила Лоренца не совершает работы (не изменяет кинетической энергии движущегося заряда), иначе говоря, при движении заряженной частицы в магнитном поле может изменяться только направление вектора скорости , но не ее модуль.

Если электрический ток создает магнитное поле, то не может ли в свою очередь магнитное поле вызвать электрический ток в проводнике? Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного потока через поверхность, ограниченную контуром, возникает электрический ток. Этот ток назвали индукционным, а само явление - электромагнитной индукцией.

Появление электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур, свидетельствует о действии в контуре сторонних сил неэлектрической природы или о возникновении ЭДС индукции при изменении магнитного потока.

Магнитным потоком Ф через поверхность площади S называют величину, равную произведению модуля вектора магнитной индукции на площадь S и на косинус угла j между вектором и нормалью к поверхности

Ф = В S cosj (7.17)

Единица магнитного потока - вебер (1Вб = 1Тл 1м²).

Опыт показывает, что направление индукционного тока в контуре зависит от того, возрастает или убывает магнитный поток, пронизывающий контур, а также от направления вектора индукции магнитного поля относительно контура. Общее правило, позволяющее определить направление индукционного тока в контуре, было установлено Ленцем: возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им магнитный поток через площадь, ограниченную контуром, стремится компенсировать то изменение магнитного потока, которое вызывает данный ток.

Тогда закон электромагнитной индукции можно сформулировать так: ЭДС индукции в замкнутом проводящем контуре пропорциональна скорости изменения магнитного потока через любую поверхность, опирающуюся на данный контур

(7.18)

Знак минус в этой формуле отражает соответствие направления индукционного тока правилу Ленца. Формула (7.18) справедлива для всех возможных случаев изменения магнитного потока. При изменении магнитного потока в катушке, состоящей из N одинаковых витков провода, общая ЭДС индукции в N раз больше ЭДС индукции в одиночном контуре, т.е.:

(7.19)

Природа ЭДС индукции была раскрыта Максвеллом. Он показал, что любое переменное во времени магнитное поле возбуждает в окружающем пространстве электрическое поле. Это поле и является причиной появления в проводнике индукционного тока. Наличие проводника лишь помогает выявить это электрическое поле. Электрическое поле, возбуждаемое переменным магнитным полем, не связано с зарядами и имеет замкнутые линии напряженности вектора (в отличие от электростатического, линии напряженности которого не замкнуты), т.е. является вихревым.

Если в переменном магнитном поле находится массивный проводник, то в его объеме под действием вихревого электрического поля возникают индукционные токи, которые называют вихревыми токами или токами Фуко. Они циркулируют в плоскостях, перпендикулярных линиям индукции магнитного поля. В сплошных проводящих телах эти токи весьма велики и приводят к сильному разогреву тел.

При изменении силы тока в контуре изменяется и созданное им магнитное поле, а потому в этом контуре также индуцируется ЭДС, которую называют ЭДС самоиндукции. Так как вектор магнитной индукции пропорционален силе тока (см. Закон Био-Савара-Лапласа), то и магнитный поток пропорционален силе тока I, т.е.

Ф=LI (7.20)

где L - коэффициент, зависящий от формы контура, его размеров и магнитных свойств среды (m), он называется индуктивностью контура.

Если за время dt ток в контуре изменился на dI, то изменение магнитного потока

dФ=LdI.

По закону электромагнитной индукции (7.18) в контуре при этом появится ЭДС самоиндукции

(7.21)

Индуктивность - коэффициент L, численно равный ЭДС самоиндукции, возникающей в контуре при изменении в нем силы тока, равном единице за единицу времени.

Единица индуктивности - Генри (1Гн= ).

Вычислим индуктивность L соленоида, длина которого ℓ, а число витков N, каждый из которых ограничивает площадь S и имеющего сердечник с магнитной проницаемостью m.

Магнитный поток, пронизывающий все витки соленоида, называют потокосцеплением и он равен

Y= ВSN=NФ

Учитывая, что В=m₀mN и выражение для магнитного потока (7.20), получим

LI=m₀mHSN,

а согласно (7.14) окончательно имеем

L = m₀mn²V (7.22)

где V-объем соленоида, n-число витков, приходящихся на единицу длины соленоида.

Явление возбуждения ЭДС в одном контуре при изменении силы тока в другом контуре называют взаимной индукцией. Магнитная связь двух контуров (1 и 2) характеризуется взаимной индуктивностью L₁₂, которая определяет значение ЭДС взаимной индукции в одном контуре при изменении силы тока в другом контуре. Взаимная индуктивность L₁₂ зависит от относительного расположения, размеров, формы контуров и магнитной проницаемости среды.

На явлении взаимной индукции основано действие трансформатора - устройства для повышения или понижения переменного напряжения.

 

Описание лабораторной установки

Соленоид имеет длину ℓ =0,43 м, диаметр 50мм и число витков N=200.

Для измерения магнитной индукции используется зонд, представляющий собой катушку диаметром d =9,2 мм, а число ее витков N₁ =1500. Принцип действия зонда основан на явлении электромагнитной индукции (7.19)

(7.23)

где S -площадь сечения катушки.

В связи с тем, что индукция В внутри соленоида, по которому протекает переменный ток, изменяется по гармоническому закону

В=В_mcoswt,

то соотношение (7.23) примет вид

e=N₁SwB_msinwt (7.24)

где w -циклическая частота.

При изменении напряжения прибором с большим входным сопротивлением можно считать, что измеряемое прибором напряжение U равно e, т.е.

e=U=U_msinwt.

Тогда из формулы (7.23) с учетом, что w=2pn, следует

(7.25)

где U_m -амплитудное значение напряжения, n=50 гц.

 

Выполнение работы

Задание 1. Снять зависимость индукции В в центре соленоида от силы тока I, протекающего по обмотке соленоида, B₀(I); N=200.

Для этого соберите схему рис.7.4,

Рис. 7.4

где 1-соленоид, 2-зонд. Установите зонд в центре соленоида. Изменяя силу тока I, проходящего через соленоид, провести измерения значений напряжения U_эф с помощью милливольтметра (mV) или осциллографа.

Используя формулу (7.25), рассчитайте индукцию магнитного поля в центре соленоида в зависимости от силы тока I (U_m=U_эф× ). Результаты измерений и расчетов занести в таблицу. Зная индукцию магнитного поля В, рассчитать напряженность магнитного поля Н соленоида по формуле (7.14). Результаты расчетов занести в таблицу.

Построить зависимость В=В(I) и Н=Н(I), отложив на оси абсцисс силу тока I.

Задание 2. Снять зависимость индукции В(ℓ) соленоида от положения зонда на оси соленоида (N=100).

Собрать схему рис.7.4. Установить ток в цепи I=1,25А. Перемещая зонд вдоль оси соленоида (шаг 1 см) провести измерения значений напряжения U_эф с помощью милливольтметра (mV) или осциллографа. Используя формулы 7.13 и 7.25, определить индукцию магнитного поля для всех положений зонда на оси соленоида.

Результаты измерений и расчетов занести в таблицу. Построить зависимость В=В(ℓ), отложив на оси абсцисс расстояние ℓ.

Задание 3. Из полученной зависимости В=В(I), задание 1, определить коэффициент пропорциональности a между В и nI (см. формулу 7.14)

сравнить полученное значение a с постоянной m₀.

 

Контрольные вопросы

1. Схема установки и порядок выполнения работы.

2. Как создаются и обнаруживаются магнитные поля? Индукция и напряженность магнитного поля. Единицы измерения. Линии магнитной индукции. Принцип суперпозиции магнитных полей.

3. Магнитная проницаемость среды. Связь вектора с вектором . Сформулируйте закон Био-Савара-Лапласа. Рассчитайте индукцию магнитного поля прямолинейного проводника с током.

4. Запишите силу Ампера и силу Лоренца. Как они направлены? Чему равна работа силы Лоренца над зарядом?

5. Выведите формулу для индукции и напряженности магнитного поля бесконечно длинного соленоида. Выведите формулу (7.25).

6. Дайте определение магнитного потока. Сформулируйте закон электромагнитной индукции. Как направлен индукционный ток?

7. Токи Фуко. Явление самоиндукции. Индуктивность соленоида (7.22). Явление взаимной индукции. Вихревое электрическое поле.