Теоремы о пределах функций
Теорема №1: Предел постоянной функции 
существует в каждой точке 
и равен постоянной с, то есть 
.
Теорема №2: Предел функции у = х в каждой точке равен х0.
| х |
| у |
| с |
| у |
| х |
| у |
| х |
.
Рис. 1. 
Рис. 2. 
Рис. 3. 
2.2. Свойства пределов функций
- Функция не может иметь двух разных пределов в точке.
- Предел алгебраической суммы функций равен алгебраической сумме пределов этих функций, если последние существуют.
- Предел произведения функций равен произведению пределов этих функций, если последние существуют.
- Постоянный множитель можно вынести за знак предела.
- Предел частного функций равен частному пределов этих функций, если последние существуют и предел второй функции не равен нулю.
- Пусть в некоторой окрестности точки х0, за исключением, может быть, самой точки х0, выполняется неравенство
.
Тогда, если 
, 
, то 
.
Пример:
1. Найти 
, если 
.
Решение: 
.
Ответ: 
.
2. Найти 
, если .
Ответ: 
.
3. Найти 
, если 
, 
.
Ответ: 
.
4. Найти 
, если 
, 
.
Ответ: 
.
5. Вычислить 
. Ответ: 
.
6. Вычислить 
. Ответ: 
.
7. Вычислить 
. Ответ: 
.
2.3. Односторонние пределы
В определении предела функции считается, что х стремится к х0 любым способом: слева от х0, справа от х0, колеблясь около х0.
Однако, бывают случаи, когда способ приближения аргумента х к х0 существенно влияет на значение предела функции. Поэтому введены понятия односторонних пределов.
- предел функции 
слева в точке х0;
- предел функции 
справа в точке х0;
Если существует , то существуют и оба односторонних предела, причём А=А1=А2.
| у |
| х |
| А1 |
| A2 |
| х0 |
и 
, и они равны, то существует .|
|
Если существуют односторонние пределы 
и 
, и они не равны, то 
не существует.
Упражнения: Вычислить:
1. 
, если ; 3. 
;
2. 
, если ; 4.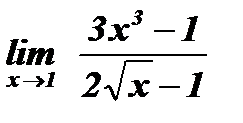 
.
3. Определение функции непрерывной в точке и на промежутке
3.1. Определение функции непрерывной в точке
Понятие непрерывности функции удобно связать с представлением о графике этой функции как о «неразрывной» (сплошной) линии. Сплошной линией будем считать линию, начерченную без отрыва карандаша от бумаги.
| х |
| у |
| А |
| х0 |
| у |
| х |
| А |
| f (x0) |
| х0 |
| у |
| х |
| f (x0) |
| х0 |
| у |
| х |
| A |
| х0 |
| f (x0) |
| у |
| х |
| f (x0) |
| х0 |
Рис. 4. Рис. 5.
Ответ: Из данных функций непрерывной является функция, изображенная на рисунке №3, так как ее график - «неразрывная» (сплошная) линия.
Вопрос: Какими свойствами обладает функция, изображенная на рисунке №3, и не обладают другие функции?
Ответ:
- Функция определена в точке х0. Это свойство не выполняется для функции, изображенной на рисунке №1.
- Существует конечный предел функции в точке х0.Это свойство не выполняется для функций, изображенных на рисунках №2, 5.
- Предел функции в точке х0равен значению функции в этой точке, то есть
. Это свойство не выполняется для функции, изображенной на рисунке №4.
Свойства, которые выполняются для функции, изображеннойна рисунке №3, и дают возможность дать определение функции непрерывной в точке х0.
Определение: Функция 
называется непрерывной в точке х0, если .
|
|
Замечание: Если функция является непрерывной в точке х0, то точка х0 называется точкой непрерывности функции, если функция не является непрерывной в точке х0, то точка х0 называется точкой разрыва функции.
Пример:
- Функция непрерывна в каждой точке , так как .
- Функция у = х непрерывна в каждой точке , так как .
- Функция
непрерывна в каждой точке 
, так как 
.
Пример: Является ли функция непрерывной в точках х1, х2, х3, х4, х5, х6, х7?
| у |
| х |
| х1 |
| х2 |
| х3 |
| х4 |
| х5 |
| х6 |
| х7 |
Ответ: Функция является непрерывной в точках х2, х7, функция не является непрерывной в точках х1, х3, х4, х5, х6.
3.2. Свойства непрерывных функций
- Если функции и
непрерывны в точке х0, то в этой точке непрерывны:
1)  ;
2)  ;
| 3)  ,  ;
4)  , 
|
- Функция
непрерывна в любой точке при любом натуральном п. - Многочлен
является непрерывной функцией в любой точке . - Дробно-рациональная функция
является непрерывной функцией в любой точке 
. - Все основные элементарные функции непрерывны в своей области определения.
Определение: Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
4. Вычисление пределов функций в точке
4.1. Вычисление пределов функций с помощью свойств пределов функций
Пример:
1) 
;
2) 
;
3) 
.
4.2. Вычисление пределов функций с помощью определения функции непрерывной в точке
Пример:
1) Вычислить 
.
Решение:
Функция 
непрерывна в точке 
, так как знаменатель дроби при 
отличен от нуля. Следовательно, 
.
2) Вычислить 
.
Решение:
Функция 
непрерывна в точке 
, так как область определения показательной функции 
- множество всех действительных чисел R. Следовательно, 
.
|
|
Вывод: Если известно, что функция непрерывна в точке х0, то для нахождения 
нужно вычислить 
.
4.3. Вычисление пределов функций при наличии неопределенности вида 
.
Замечание: Если при вычислении 
и 
, то говорят, что имеет место неопределенность вида . Теорема о пределе частного не применима, поэтому дробь необходимо преобразовать.
Пример:
1) 
;
Решение:
; 
. Имеет место неопределенность вида . Преобразуем дробь, для этого числитель и знаменатель данной дроби разложим на множители по формуле: 
, где х1, х2- корни квадратного трехчлена 
.
, 
, 
, 
, 
.
, 
, 
, 
, 
.
.
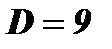Функция 
непрерывна в точке , так как знаменатель дроби при отличен от нуля. Следовательно, 
.
Ответ: 
.
2) 
;
Решение:
; 
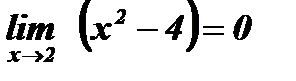. Имеет место неопределенность вида . Преобразуем дробь, для этого числитель и знаменатель данной дроби разложим на множители с помощью формул сокращенного умножения:
, 
.
.
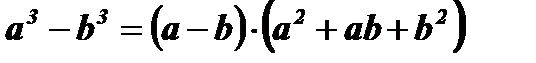Функция 
непрерывна в точке 
, так как знаменатель
дроби при 
отличен от нуля. Следовательно, 
.
Ответ: 
.
3) 
.
Решение:
, 
. Имеет место неопределенность вида .