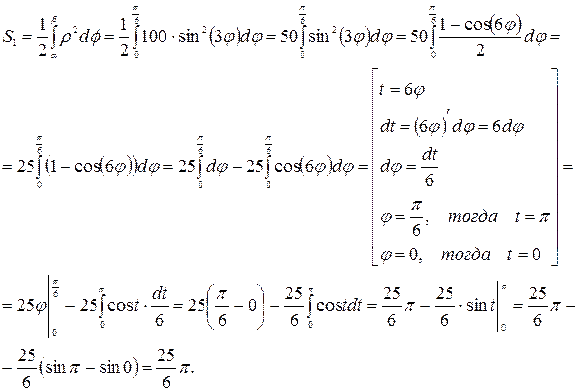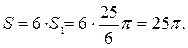Вычисление площади плоской фигуры
(задание 5)
С помощью определенного интеграла вычислить площадь фигуры, ограниченной линиями.
Вычисление плоской фигуры в декартовой системе координат
Пусть на отрезке 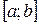 задана непрерывная функция
задана непрерывная функция 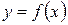 , причём
, причём  . Фигура, ограниченная сверху графиком
. Фигура, ограниченная сверху графиком 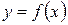 , снизу – осью Оx, сбоку прямыми
, снизу – осью Оx, сбоку прямыми  ,
,  (рис. 1а), называется криволинейной трапецией.
(рис. 1а), называется криволинейной трапецией.
Геометрическим смыслом определённого интеграла являетсяплощадь криволинейной трапеции вычисляется по формуле
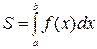 .
.
Если фигура, площадь которой необходимо вычислить, ограничена сверху графиком функции 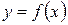 , снизу – графиком функции
, снизу – графиком функции 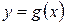 , а сбоку прямыми
, а сбоку прямыми  ,
,  (рис 1.б), то её площадь вычисляется по формуле
(рис 1.б), то её площадь вычисляется по формуле
 .
.
Частным случаем при этом является нахождение площади фигуры, ограниченной сверху осью Оx, снизу – графиком функции 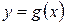 , а сбоку прямыми
, а сбоку прямыми  ,
,  (рис 1.в). В этом случае, в предыдущую формулу следует подставлять
(рис 1.в). В этом случае, в предыдущую формулу следует подставлять 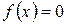 , тогда формула для вычисления площади такой фигуры имеет вид
, тогда формула для вычисления площади такой фигуры имеет вид
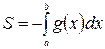 .
.
В некоторых случаях, чтобы вычислить площадь искомой фигуры, необходимо разбить ее на сумму или разность двух или более криволинейных трапеций (рис. 1г).
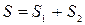 , где
, где 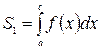 ,
, 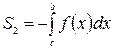 .
.
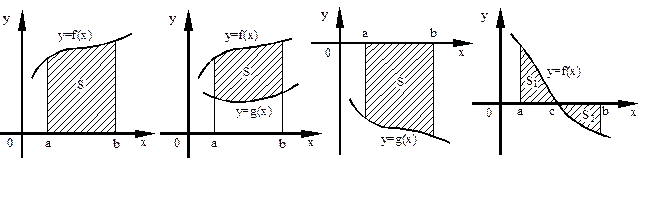
а) б) в) г)
Рис. 1
Пример 25
Вычислить площадь фигуры, ограниченной графиками функций 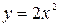 ,
, 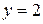 .
.
Решение
1. Вершиной параболы 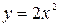 является точка
является точка 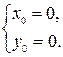
2. Точки пересечения параболы и прямой находятся из системы 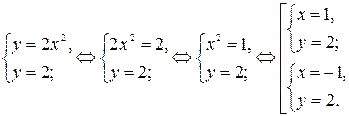
3. Используя найденные точки, строим графики заданных функций в декартовой системе координат.
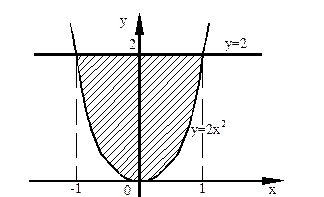 4. Сверху фигура ограничена прямой
4. Сверху фигура ограничена прямой 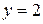 , значит
, значит 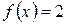 , снизу – параболой, значит
, снизу – параболой, значит  .
.
По графику видно, что  ,
,  .
.
1способ: площадь полученной фигуры можно вычислить по формуле:
Рис. 2
 2 способ: полученная фигура симметрична, значит
2 способ: полученная фигура симметрична, значит

Пример 26
Вычислить площадь фигуры, ограниченной кривой 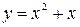 , прямыми
, прямыми 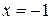 ,
, 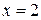 и осью Оx.
и осью Оx.
Решение
1. Вершиной параболы 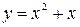 является точка
является точка 
Замечание: координаты вершины параболы 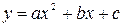 ,
, 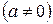 находятся по формулам
находятся по формулам 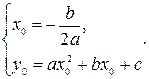
2. Точка пересечения параболы и прямой 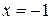 находится из системы
находится из системы 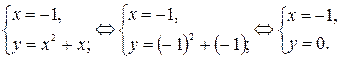
Точка пересечения параболы и прямой 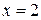 находится из системы
находится из системы 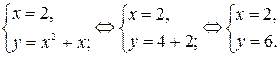
Точки пересечения параболы с осью Оx ( ) находятся из системы
) находятся из системы 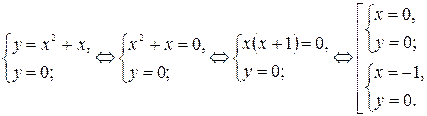
3. Используя найденные точки, строим графики заданных функций в декартовой системе координат.
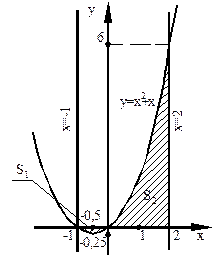 4. Площадь искомой фигуры
4. Площадь искомой фигуры  складывается из площадей
складывается из площадей 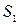 и
и  .
.
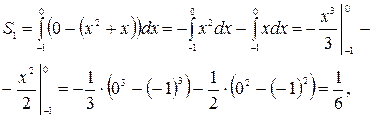

Рис. 3 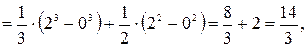
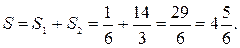
Если фигура, площадь которой необходимо вычислить, ограничена слева осью Oy, справа – графиком функции  , а снизу и сверху прямыми
, а снизу и сверху прямыми 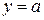 ,
, 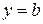 соответственно (рис. 4а), то её площадь вычисляется по формуле
соответственно (рис. 4а), то её площадь вычисляется по формуле
 .
.
Если фигура, площадь которой необходимо вычислить, ограничена слева графиком функции 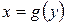 , справа – графиком функции
, справа – графиком функции  , а снизу и сверху прямыми
, а снизу и сверху прямыми 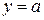 ,
, 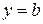 соответственно (рис. 4б), то её площадь вычисляется по формуле
соответственно (рис. 4б), то её площадь вычисляется по формуле
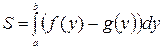 .
.
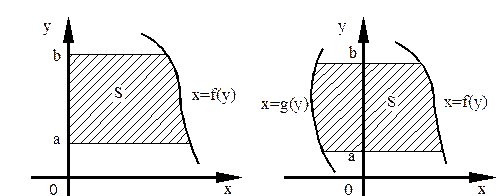
а) б)
Рис. 4
Пример 27
Вычислить площадь фигуры, ограниченной кривой 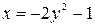 , прямой
, прямой  и осями координат.
и осями координат.
Решение
1. Вершиной параболы 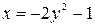 является точка
является точка 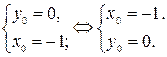
Замечание: координаты вершины параболы 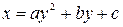 ,
, 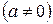 находятся по формулам
находятся по формулам 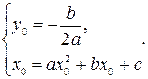
2. Точка пересечения параболы и прямой  находится из системы
находится из системы 
Точка пересечения параболы с осью Оx ( ) находится из системы
) находится из системы 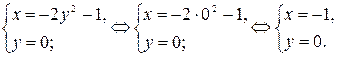
Точка пересечения параболы с осью Оy (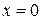 ) находится из системы
) находится из системы  нет решения
нет решения
3. Используя найденные точки, строим графики заданных функций в декартовой системе координат.

Рис. 5
4. Слева фигура ограничена параболой, справа – осью Oy, снизу – прямой  , сверху – осью Оx Таким образом, подставляя в формулу 6:
, сверху – осью Оx Таким образом, подставляя в формулу 6: 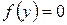 ,
, 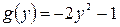 ,
,  ,
,  , получим
, получим
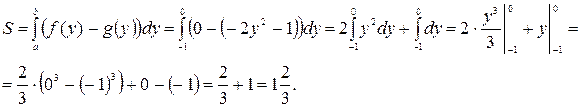
Вычисление площади плоской фигуры в полярной системе координат
Возьмём на плоскости произвольную точку О (полюс) и проведём луч Ох (полярная ось). Примем какой-либо отрезок ОА за единицу длины и какой-либо угол (обычно берётся радиан) за единицу измерения углов. Тогда положение любой точки М на плоскости можно задать двумя числами:
1. числом  – полярный угол (он имеет положительное значение при повороте против часовой стрелки);
– полярный угол (он имеет положительное значение при повороте против часовой стрелки);
2. положительным числом  – полярный радиус.
– полярный радиус.
Пара чисел  – это полярные координаты точки М.
– это полярные координаты точки М.
Каждой паре значений  отвечает только одна точка, но одной и той же точке М отвечает бесчисленное множество значений полярного угла, отличающихся друг от друга на число, кратное
отвечает только одна точка, но одной и той же точке М отвечает бесчисленное множество значений полярного угла, отличающихся друг от друга на число, кратное  .
.
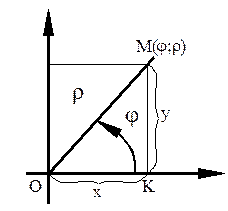
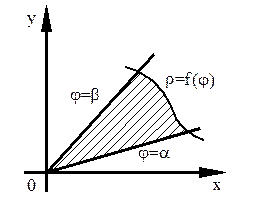
а) б)
Рис. 6
Связь между полярными и прямоугольными координатами
Из треугольника OMK (рис. 6а) получаются следующие соотношения:
– переход из декартовой в полярную систему координат
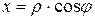 ,
, 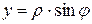 ;
;
– переход из полярной в декартову систему координат
 ,
, 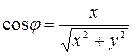 ,
,  .
.
Вычисление площади фигуры в полярной системе координат
Площадь сектора, ограниченного кривой 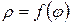 , лучами
, лучами 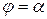 ,
, 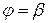 , где
, где 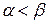 (рис. 6б), находится по формуле
(рис. 6б), находится по формуле 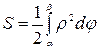 .
.
Пример 28
Вычислить площадь фигуры, ограниченной графиком функции 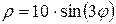 .
.
Решение
Чтобы найти пределы интегрирования 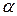 и
и 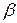 , необходимо построить график кривой
, необходимо построить график кривой 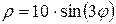 в полярных координатах. Результаты вычислений занесем в таблицу 3.
в полярных координатах. Результаты вычислений занесем в таблицу 3.
Таблица 3

| 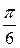
| 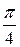
| 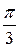
| 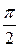
| 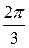
| 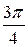
| 
| 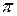
| |

| 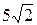
| -10 | 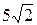
| ||||||

| 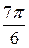
| 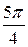
| 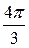
| 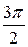
| 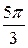
| 
| 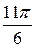
| 
| |

| -10 | 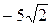
| 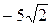
| -10 |
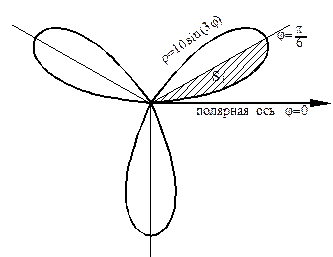 По данным этой таблицы построим график функции, откуда видим, что площадь искомой фигуры
По данным этой таблицы построим график функции, откуда видим, что площадь искомой фигуры 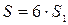 .
.
Рис. 7