Глава X. Кривые 2-го порядка на плоскости.
Определение 1. Кривой второго порядка  на плоскости называется линия, определяемая в заданной аффинной системе координат
на плоскости называется линия, определяемая в заданной аффинной системе координат 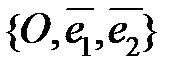 уравнением вида
уравнением вида
а11x2+a22y2+2a12xy+2a13x+2a23y+a33 =0
в котором по крайней мере один из коэффициентов a11, a12, a22 отличен от нуля.
Определение 2. В аффинной системе координат 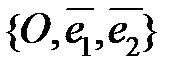 на плоскости
на плоскости
точкой называется любая пара чисел (x,y), где x ∈ℂ, y ∈ℂ.
При этом, если x ∈ℝ и y ∈ℝ, точка (x,y) называется действительной точкой плоскости, а если x ∉ℝ или y ∉ℝ, то мнимой точкой плоскости.
Замечание 1. Некоторым уравнениям, указанным в определении 1, могут удовлетворять лишь мнимые точки плоскости, некоторым – как действительные так и мнимые. На чертеже действительные точки изображаются, а мнимые – нет.
Теорема 1. Для произвольной кривой второго порядка  существует такая декартова прямоугольная система координат
существует такая декартова прямоугольная система координат  , что в этой системе кривая
, что в этой системе кривая  имеет уравнение одного из следующих канонических видов:
имеет уравнение одного из следующих канонических видов:
| Кривая | Каноническое уравнение | Количество действительных точек | |
| Эллипс |  , , 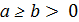
| Бесконечное множество | |
| Мнимый эллипс | 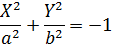
| Нет | |
| Две мнимые пересекающиеся прямые | 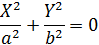
| Одна, (0,0) | |
| Гипербола | 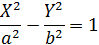
| Бесконечное множество | |
| Две пересекающиеся прямые | 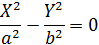
| Бесконечное множество | |
| Парабола | 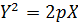
| Бесконечное множество | |
| Две параллельные прямые | 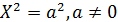
| Бесконечное множество | |
| Две мнимые параллельные прямые | 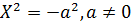
| Нет | |
| Две совпадающие прямые | 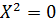
| Бесконечное множество |
В этих уравнениях 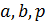 — положительные действительные параметры.
— положительные действительные параметры.
Далее рассмотрим некоторые частные случаи кривых второго порядка на плоскости.
Окружность.
|
|
Определение 3. Окружностью называется фигура, состоящая из всех точек плоскости, равноудаленных от данной точки М 0 , называемой центром на расстояние R, называемое радиусом.
| x |
| y |
| M0 |
| M |
| R |
| 0 |
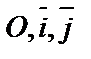 } M0= (x0,y0) – центр окружности γ.
} M0= (x0,y0) – центр окружности γ.
1) 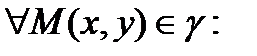
 - радиусу окружности, т.е.
- радиусу окружности, т.е. 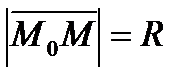 .
.
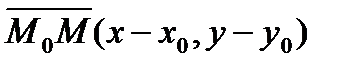 ;
; 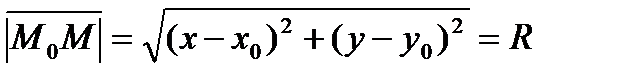
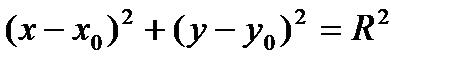 (1) – уравнение окружности с центром M0= ( x0,y0 ) и радиусом R.
(1) – уравнение окружности с центром M0= ( x0,y0 ) и радиусом R.
2) Обратно, если числа x,y удовлетворяют (1), то для точки 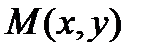 выполняется
выполняется 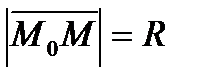
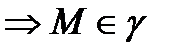 . Таким образом (1) является уравнением окружности γ.
. Таким образом (1) является уравнением окружности γ.
Эллипс.
| F 2(с,0) |
| x |
| y |
| M (x,y) |
| F 1(- с,0) |
Определение 4. Эллипсом называется фигура, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек F 1 и F 2 есть величина постоянная, большая, чем расстояние между F 1 и F 2.
Точки F 1 и F 2 называются фокусами эллипса.
Таким образом, если γ – эллипс, то

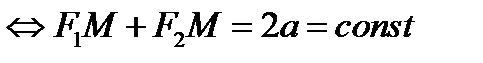 (2).
(2).
Причем 2 a >2 c, то есть а > c.
Выберем систему координат такую что Ox проходит через F 1 и F 2, 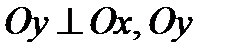 проходит через середину отрезка F 1 F 2. Тогда F 1(-c,0), F 2(c,0).
проходит через середину отрезка F 1 F 2. Тогда F 1(-c,0), F 2(c,0).
1. Пусть 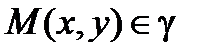 - произвольная точка эллипса
- произвольная точка эллипса
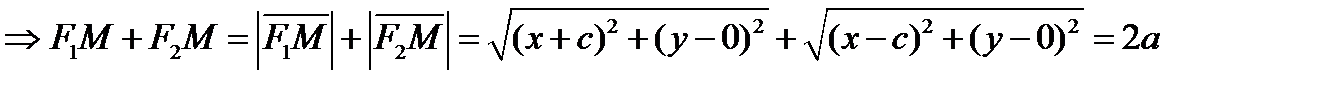
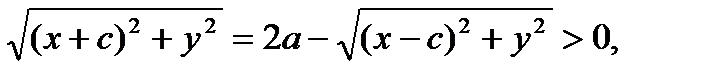 так как
так как 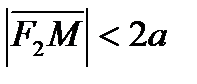 .
.
Возведем в квадрат обе части последнего равенства: 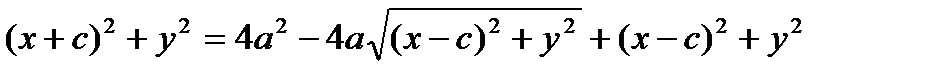 ;
;  ;
; 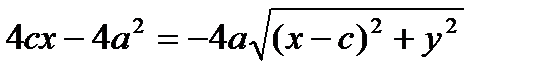 |: (–4);
|: (–4);
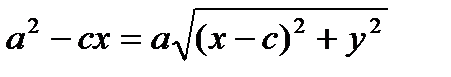 >0. Снова возводя в квадрат обе части, получим:
>0. Снова возводя в квадрат обе части, получим:
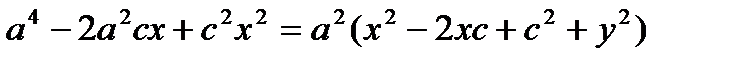 ;
;
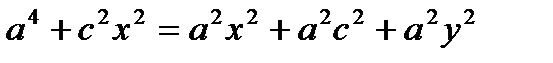 ;
;
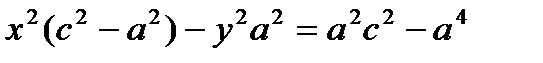 ;
;
 |:
|:  ;
;
 . Обозначим
. Обозначим 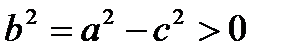 .
.
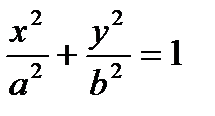 (3) – каноническое уравнение эллипса.
(3) – каноническое уравнение эллипса.
2. Обратно покажем, что если числа x 1, y 1 удовлетворяют (3), то точка M 1(x 1 ,y 1) принадлежит эллипсу, то есть выполняется (2) 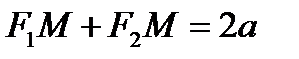 .
.
Из 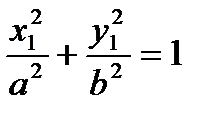 выразим
выразим 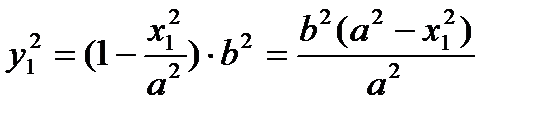
Тогда 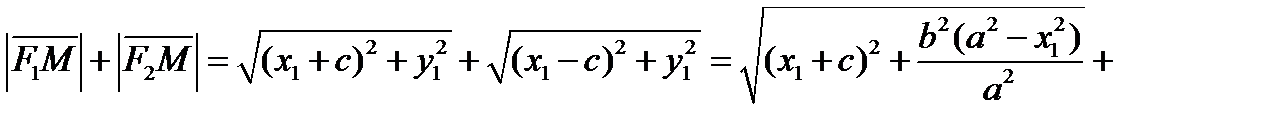
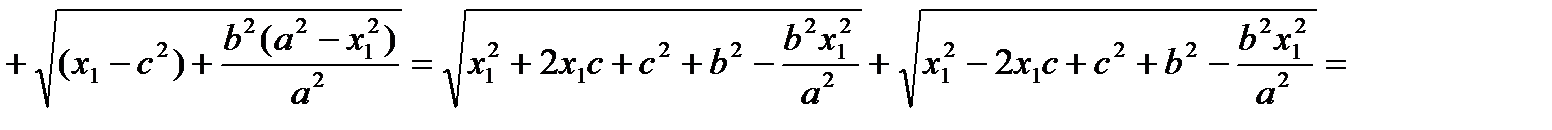
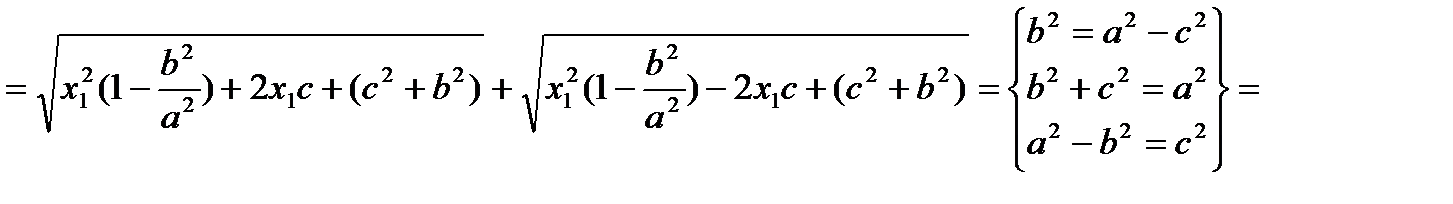
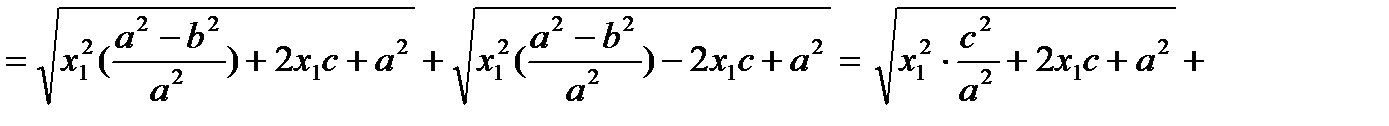
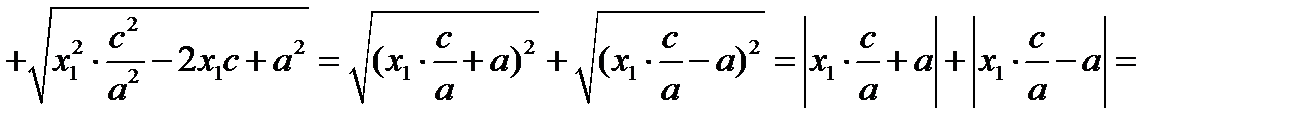
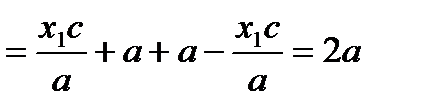 . Что и требовалось доказать. При этом для выражений под знаком модуля справедливо:
. Что и требовалось доказать. При этом для выражений под знаком модуля справедливо:
|
|
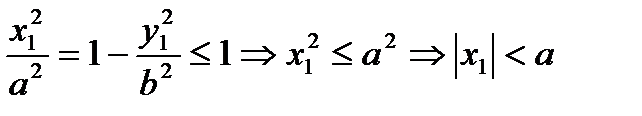
 .
.
Значит, если 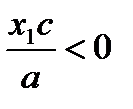 , то из
, то из 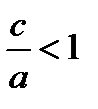 и
и 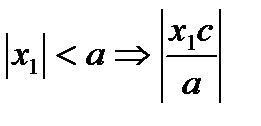 не превысит а. Поэтому
не превысит а. Поэтому  и первый модуль нужно раскрывать со знаком «плюс».
и первый модуль нужно раскрывать со знаком «плюс».
Из 1. и 2. ⇒ Уравнение (3) является уравнением эллипса в выбранной системе координат.
| F 2 |
| x |
| y |
| F 1 |
| -a |
| a |
| -b |
| b |
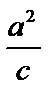
|
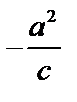
|
| c |
| -c |
| K |
| M |
a – большая полуось эллипса, b – малая полуось эллипса.
Фокальное расстояние эллипса 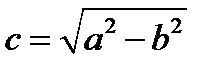 .
.
Эксцентриситет эллипса – число 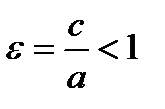 .
.
Директрисы эллипса – две прямые, параллельные малой оси, отстоящие от нее на расстоянии 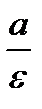 , то есть прямые
, то есть прямые 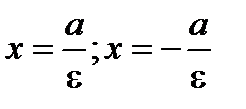 .
.
Геометрический смысл директрисы: отношения расстояния от любой точки эллипса до фокуса к расстоянию от нее до соответствующей директрисы постоянно и равно эксцентриситету ε, т.е  .
.
Гипербола.
| F 2(с,0) |
| x |
| y |
| M (x,y) |
| F 1(- с,0) |
Определение 5. Гиперболой называется фигура, состоящая из всех точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая, чем расстояние между точками F1 и F2.
Точки F1 и F2 называются фокусами гиперболы.
Таким образом, если γ –гипербола, то
 ⇔
⇔  (4),
(4),
причем 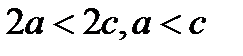 .
.
Выберем прямоугольную систему координат такую что Ox проходит через F1 и F2, 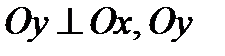 проходит через середину F 1 F 2. Тогда
проходит через середину F 1 F 2. Тогда  .
.
1. Пусть 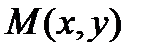 произвольная точка гиперболы, то есть выполняется (4).
произвольная точка гиперболы, то есть выполняется (4).
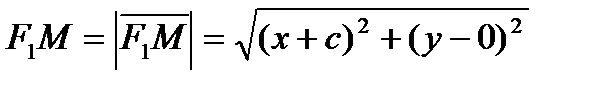 ,
, 
(4) 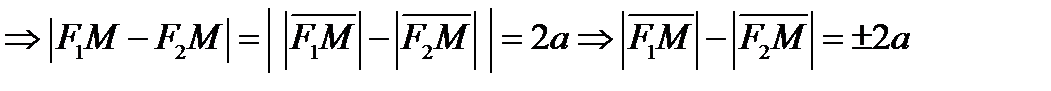 .
.

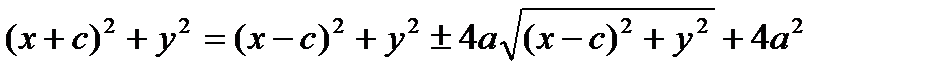
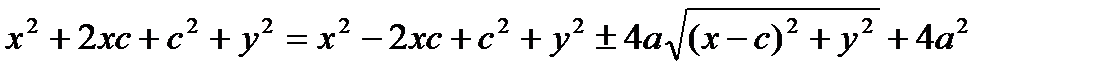
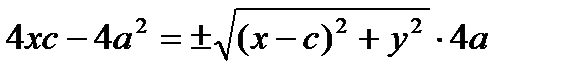
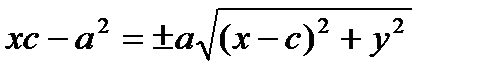
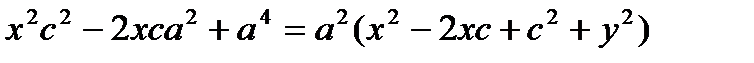

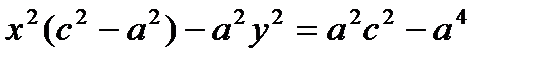 |:
|: 
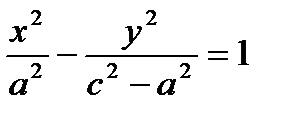 Так как
Так как 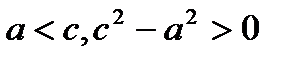 , то обозначим
, то обозначим 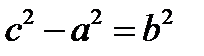 .
.
Таким образом получим
 (5) – каноническое уравнение гиперболы.
(5) – каноническое уравнение гиперболы.
|
|
2. Обратно, покажем, что если числа x1 и y1 удовлетворяют уравнению (5), то точка M1 (x1,y1) принадлежит гиперболе, то есть выполняется (4) для M1
(5) 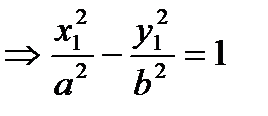 (6)
(6)
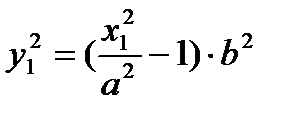
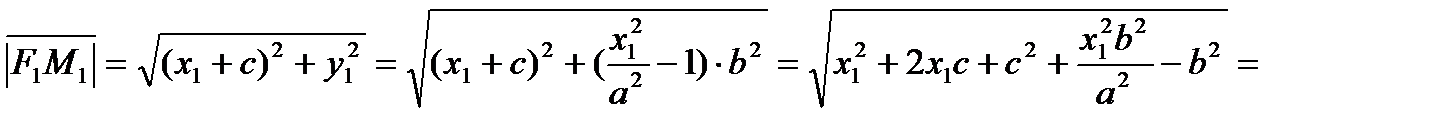
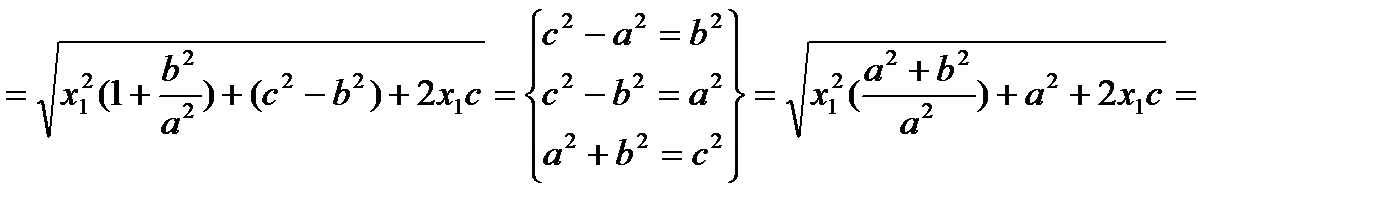
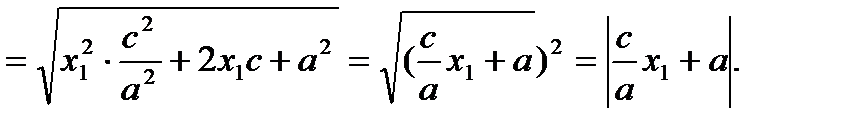
Аналогично 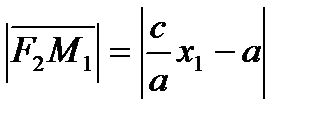 .
.
(6) 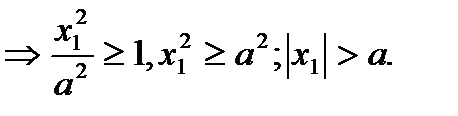 Заметим также, что
Заметим также, что  .
.
При 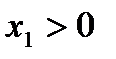
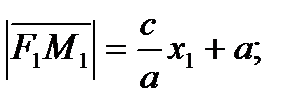 так как
так как 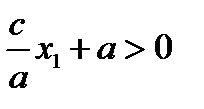 .
.
Из 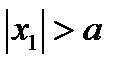 и
и 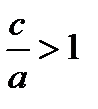 следует
следует  и
и 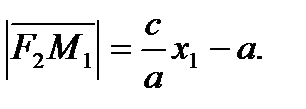
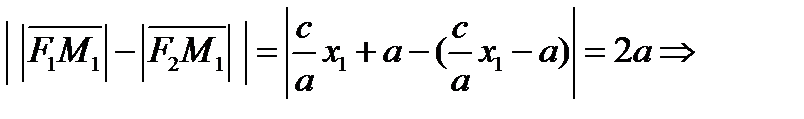 выполняется (4)
выполняется (4)
При 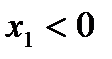 из
из 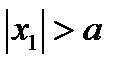 и
и 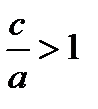 следует
следует 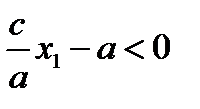 и
и 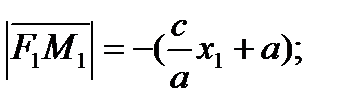
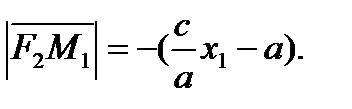
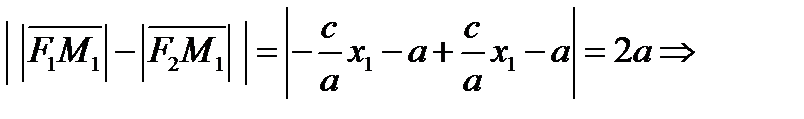 выполняется (4)
выполняется (4)
Таким образом 1.,2. ⇒ уравнение (5) является уравнением гиперболы.
| F 2(с,0) |
| x |
| y |
| F 1(- с,0) |
| -a |
| a |
| -b |
| b |
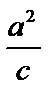
|
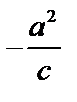
|
а – действительная полуось гиперболы;
b – мнимая полуось гиперболы.
Эксцентриситет гиперболы – число 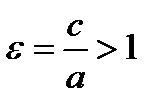
Асимптоты гиперболы – прямые 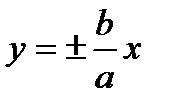
Директрисы гиперболы – прямые 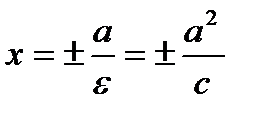 , их геометрический смысл определяется аналогично директрисам эллипса:
, их геометрический смысл определяется аналогично директрисам эллипса:
отношения расстояния от любой точки гиперболы до фокуса к расстоянию от нее до соответствующей директрисы постоянно и равно эксцентриситету ε.
Парабола.
Пусть на плоскости дана точка F и прямая l. F ∉ l. Расстояние d (F, l) =p.
Определение 6. Параболой называется фигура, состоящая из всех точек плоскости, каждая из которых равноудалена от данной точки F и данной прямой l. При этом F называется фокусом параболы, l – директрисой.
Таким образом, если γ –парабола, то
M Îg⇔ MF = d (M, l)= MK (7),
F 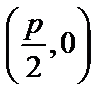
|
| l |
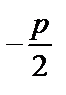
|
| x |
| y |
K 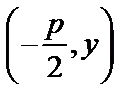
|
| M (x,y) |
Выберем прямоугольную систему координат, такую что 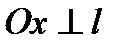 ,
, 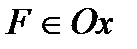 .
.
Oy || l. проходит на расстоянии 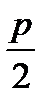 от F и l. Тогда
от F и l. Тогда 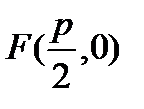 , уравнение
, уравнение 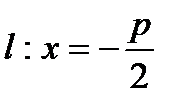 .
.
1. Пусть 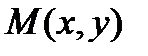 - произвольная точка параболы ⇒ выполняется (7)
- произвольная точка параболы ⇒ выполняется (7)

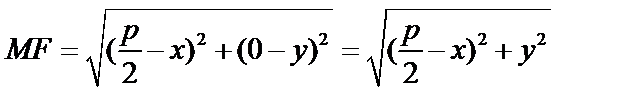
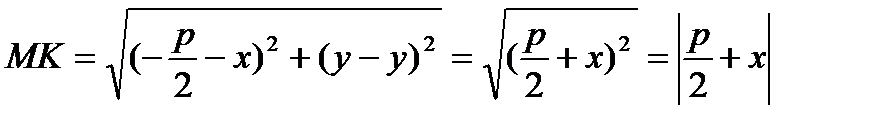
(7) 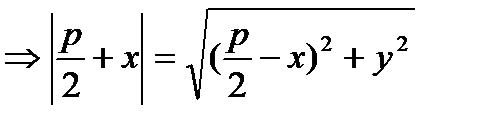 возведём в квадрат.
возведём в квадрат. 
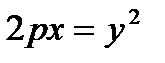 .
.
 (8) – каноническое уравнение параболы
(8) – каноническое уравнение параболы
2. Обратно, пусть числа 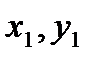 удовлетворяют (8), покажем, что точка
удовлетворяют (8), покажем, что точка  -параболе, то есть выполняется (7).
-параболе, то есть выполняется (7).
(8) 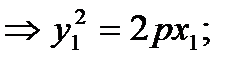
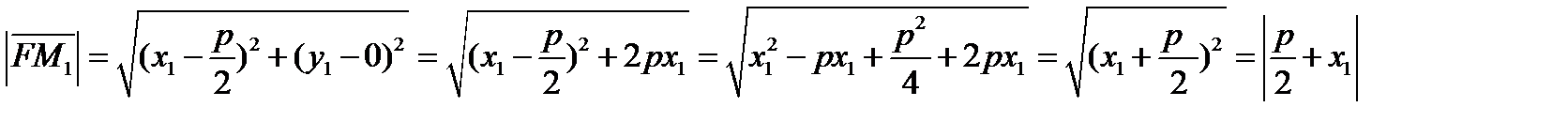
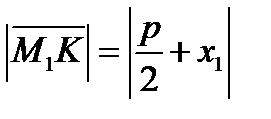
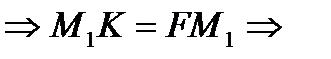 выполняется (7).
выполняется (7).
Таким образом, 1.,2. ⇒ уравнение (7) является уравнением параболы.
| y |
F 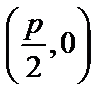
|
| l |
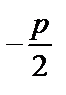
|
| x |
K 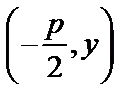
|
| M (x,y) |
| 0 |
Приведение произвольного уравнения кривой второго порядка
К каноническому виду.
Рассмотрим произвольное уравнение кривой второго порядка относительно прямоугольной декартовой системы координат {O,  ,
, 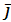 }.
}.
а11x2+a22y2+2a12xy+2a13x+2a23y+a33 =0 (8).
В матричном виде уравнение (8) можно записать так:
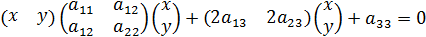 (9)
(9)
Заметим, что первые три слагаемых в (8) представляют собой квадратичную форму от переменных x и y: f (x,y) =а11x2+a22y2+2a12xy.
Матрица этой квадратичной формы имеет вид А=  .
.
Применим к базису {  ,
, 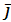 }. ортогональный линейный оператор c матрицей Т=
}. ортогональный линейный оператор c матрицей Т=  , то есть перейдем от базиса {
, то есть перейдем от базиса {  ,
, 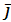 } к базису {
} к базису { 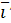 ,
, 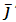 }.по формулам
}.по формулам
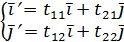 .. (10)
.. (10)
Тогда в системе координат {O, 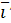 ,
, 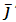 } уравнение (9) примет вид
} уравнение (9) примет вид
 (11)
(11)
Коэффициенты 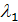 и
и 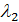 в уравнении (11) находятся как собственные значения матрицы А=
в уравнении (11) находятся как собственные значения матрицы А=  .
.
Столбцы матрицы Т: T1= 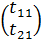 и T2=
и T2= 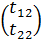 могут быть получены как нормированные собственные векторы матрицы А, принадлежащие собственным значениям
могут быть получены как нормированные собственные векторы матрицы А, принадлежащие собственным значениям 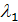 и
и 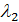 .
.
Далее, выделяя в полученном уравнении (11) полные квадраты, можно привести его к одному из видов, указанных в Теореме 1.