МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Политехнический институт
Кафедра «Инструментальные и метрологические системы»
Методические указания
По Контрольно-курсовой работе
по дисциплине
ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ
Направление подготовки 27.03.01 «Стандартизация и метрология»
Профиль подготовки «Метрология и метрологическое обеспечение»
Квалификация (степень) выпускника: бакалавр
Форма обученияочная
Тула 2014 г.
Методические указания по ККР составлены доцентом Б.И. Сотовой и обсуждены на заседании кафедры «Инструментальные и метрологические системы» Политехнического института.
Протокол №1 от 29.08. 2014 г.
Зав. кафедрой ________________ О.И. Борискин
Методические указания по ККР пересмотрены и утверждены на заседании кафедры ИМСПолитехнического института.
протокол №___ от "___"____________ 20___ г.
Зав. кафедрой ________________ И.О. Фамилия
Цель выполнения контрольно-курсовой работы.
По окончании курса «Общая теория измерений» студент должен знать и уметь использовать методики обработки результатов различных видов измерений, в том числе многократных равноточных измерений, характерных для метрологических работ. Данная контрольно-курсовая работа имеет целью:
n закрепить навыки определения точечных оценок и исключения грубых погрешностей;
n выработать умение строить гистограмму, производить проверку гипотезы о нормальности закона распределения вероятности, пользуясь таблицами нормального распределения и распределения c2;
n выработать умение правильной оценки результата измерений в виде доверительного интервала.
Структура и объем контрольно-курсовой работы
«Обработка результатов многократных равноточных измерений».
Задание содержит 100 значений какой-либо физической величины, полученных при многократных равноточных измерениях.
Для полученного задания следует:
1) расположить имеющийся массив данных в вариационный ряд;
2) определить точечные оценки числовых характеристик;
3) установить наличие или отсутствие в результатах измерений грубых промахов;
4) построить гистограмму и выдвинуть гипотезу о виде закона распределения вероятности (ЗРВ) результата измерения.
5) произвести выравнивание статистического распределения в соответствии с принятым ЗРВ и построить теоретическую кривую распределения.
6) проверить гипотезу о виде закона распределения вероятности по критерию Пирсона;
7) определить ширину доверительного интервала для среднего значения на основании заданной доверительной вероятности. Результат записать в принятой форме.
Объем работы 5 - 6 листов формата А4, на одном из листов изображается гистограмма и выравнивающая кривая.
Теоретические положения
3.1. Оценка результатов измерений как случайных величин
При проведении с одинаковой тщательностью и в одинаковых условиях повторных измерений одной и той же неизменяющейся величины мы получаем результаты, некоторые из которых отличаются друг от друга, а некоторые совпадают. Такие результаты говорят о наличии в них случайных погрешностей, то есть погрешностей, изменяющихся хаотически, непредсказуемо.
Рассмотрение случайных погрешностей (и, соответственно, результатов однократных измерений) как случайных событий дает основание использовать математический аппарат теории вероятностей и математической статистики для оценки случайных погрешностей и нахождения значения измеряемой величины, более близкого к истинному значению, чем результат одного измерения.
Теория вероятностей называет случайным такое событие, которое может произойти или не произойти. Применительно к измерениям можно сказать, что при повторных измерениях в одинаковых условиях каждая из множества возможных незначительных причин случайных изменений результатов может или появиться, или не появиться. Количественная оценка объективной возможность появления события называется его вероятностью. Вероятность достоверного события равна 1, а вероятность невозможного события - 0. Эти события неслучайные; для случайных событий вероятности их появления больше нуля и меньше единицы.
Наиболее универсальным способом описания случайных величин (в том числе результатов измерений и случайных погрешностей) являются законы распределения вероятности. Законом распределения вероятности случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Если на процесс измерения действуют несколько влияющих факторов, а вклад каждого из факторов незначителен по сравнению с их суммарным воздействием, то, согласно центральной предельной теореме теории вероятностей, результат измерения физической величины «х» подчиняется нормальному закон, или закону Гаусса.
На рис. 1 показаны кривые плотности вероятности, или дифференциальной функции нормального распределения. Аналитически эта функция описывается выражением
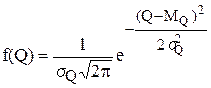(1)
Рис. 1
Здесь МQ - математической ожидание случайной величины Х, то есть такое её значение, вокруг которого группируются результаты отдельных наблюдений; при нормальном распределении математическому ожиданию соответствует наибольшая плотность вероятности.
Для непрерывной случайной величины
(2)
Для дискретной случайной величины
, (3)
где рi - вероятность значения величины Qi.
Статистической оценкой математического ожидания для ряда однородных результатов является среднее арифметическое:
(4)
sQ - среднее квадратическое отклонение случайной величины, которое представляет собой меру рассеивания значений случайной величины относительно её математического ожидания.
Dx - дисперсия случайной величины:
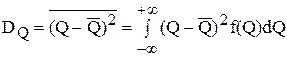
Чем больше дисперсия (или среднее квадратическое отклонение), тем значительнее рассеивание. На рис. 1 DQ2 > DQ1
Статистической оценкой среднего квадратического отклонения является так называемое стандартное отклонение:
(5)
n - число наблюдений (измерений).
Вероятность попадания случайной величины в интервал (х1, х2) равна:
(6)
что соответствует площади под кривой распределения на этом участке (рис.1)
Интервал e, который с заданной вероятностью Р покрывает истинное значение случайной величины, называется доверительным интервалом, а вероятность Р - доверительной вероятностью. Отношение доверительного интервала к среднему квадратическому отклонению - это относительный доверительный интервал:
(7)
При достаточно большом числе наблюдений (измерений) вычисленное стандартное отклонение близко к действительному значению среднего квадратического отклонения. Если при этом установлено, что закон распределения вероятности результатов измерения - нормальный, то для нахождения относительного доверительного интервала по доверительной вероятности (и наоборот, доверительной вероятности по относительному доверительному интервалу) используются математические таблицы специальной функции Лапласа. Аргументом функции Лапласа является относительный доверительный интервал, рассчитываемый по формуле:
(8)
Для того, чтобы определить вероятность попадания случайной величины (результата измерения или случайной погрешности) в интервал Q1 £ Q £ Q2, необходимо найти табличные значения F(t1) и F(t2) (аргументы t определяем по формуле (8)) и подсчитать их разность:
(9)
Если определяется вероятность попадания случайной величины в интервал 
, то:
(10)
Свойства функции Лапласа:
1) F(0) = 0
2) F(¥) = 0,5
3) F(-t) = - F(t) - функция нечетная
3.2. Обработка результатов многократных измерений
Многократные измерения одной и той же величины постоянного размера производится при повышенных требованиях к точности измерений. Если изменением измеряемой величины во времени можно пренебречь, то все значения отсчета при многократных измерениях получает один оператор с помощью одного и того же средства измерений. При этом все значения отсчета будут распределены с одинаковой дисперсией; такие значения отсчета называются равноточными (равнорассеянными).
Результат многократных измерений описывается выражением:
(11)
Как и результат однократного измерения, он является случайным значением измеряемой величины, но его дисперсия в n раз меньше дисперсии результата однократного измерения:
соответственно 
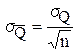(12)
То есть точность определения значения измеряемой величины повышается в 
раз.
Окончательный результат многократных измерений записывается в форме доверительного интервала
(13)
где величина t находится в зависимости от заданной доверительной вероятности.
Порядок выполнения и обработки многократных равноточных измерений следующий.
1) Анализ априорной информации.
2) Получение ряда независимых значений отсчета xi
3) Перевод отсчета в показание и внесение поправки.
4) Определение среднего значения 
и среднего квадратического отклонения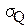 
измеряемой величины. Определенные на основании опытных данных, эти параметры называются точечными оценками. Точечные оценки вычисляются по формулам (4) и (5), приведенным в разделе 2.1.
5) Проверка наличия или отсутствия в результатах измерений грубых промахов.
6) Построение гистограммы и определение вида закона распределения вероятности результата измерения.
7) Проверка гипотезы о виде закона распределения, чаще всего о нормальности этого закона.
8) Определение ширины доверительного интервала на основании заданной доверительной вероятности.
Рассмотрим более подробно отдельные этапы этой последовательности действий.
3.2.1.Обнаружение грубых погрешностей.
Грубыми называются погрешности, явно превышающие по своему значению погрешности, оправданные условиями проведения эксперимента (измерения). Очевидно, что наиболее подозрительными являются минимальное и максимальное показания. Вопрос о том, содержит ли данный результат грубую погрешность, решается общими методами проверки статистических гипотез.
Проверяемая гипотеза состоит в утверждении, что результат Qi не содержит грубой погрешности. Для проверки этой гипотезы при достаточно большом числе измерений пользуются так называемым правилом «трех сигм». Если известно (или с достаточной вероятностью предполагается), что закон распределения - нормальный, и его числовые характеристики (их оценки) равны МQ () и sQ (SQ), то с доверительной вероятностью 0,9973 грубыми промахами являются те результаты измерения, которые выходят за границы интервала МQ ±3sQ ( ±3SQ).
После того, как грубые погрешности (промахи) исключены из результатов измерения, необходимо снова определить оценки числовых характеристик и убедиться в отсутствии грубых погрешностей.
3.2.2. Правила построения гистограммы.
При обработке экспериментальных данных на их основе часто строится гистограмма распределения. По оси абсцисс откладываются интервалы значений измеряемой величины (обычно равные), эти отрезки являются основаниями прямоугольников, площади которых равны частотам р попадания значений величины на каждый интервал (р = m/n, где m – количество результатов измерений, попавших в данный интервал). Таким образом, высота каждого прямоугольника равна частоте, деленной на длину интервала. Очевидно, что полная площадь гистограммы равна единице.
По виду гистограммы (рис.2), а также исходя из существа задачи, можно предположить принципиальный вид кривой распределения (закона распределения вероятности). Например, из рис. 2 видно, что распределение вероятности скорее всего окажется нормальным.
Pi /ΔQ 
Рис.2
Для предполагаемого распределения с вычисленными оценками числовых характеристик строится теоретическая кривая. Далее следует выяснить вопрос, являются ли расхождения теоретического и статистического распределения случайными (из-за малого числа наблюдений), или объясняются неправильно подобранным теоретическим распределением? На этот вопрос отвечают с помощью так называемых критериев согласия; наиболее распространенным из них является критерий К.Пирсона.
3.2.3. Проверка вида закона распределения по критерию Пирсона.
При использовании этого критерия за меру расхождения экспериментальных данных с теоретическим распределением принимается сумма квадратов отклонения теоретических вероятностей Pi от соответствующих частот mi/n, взятых с некоторыми коэффициентами (весами) n/Pi:
(14)
где k - число интервалов гистограммы,
mi - число результатов измерений, попавших в i-й интервал,
n - общее число наблюдений (измерений).
Если расхождение случайно, то величина c2 подчиняется т.н. c2 распределению Пирсона. Предельно допустимые значения критерия 
даны в таблицах. Если при заданной доверительной вероятности и числе степеней свободы r = k - 3 выполняется условие 
, то принимается гипотеза о соответствии распределения принятому закону, например, нормальному.
При использовании критериев согласия возможны два рода ошибок:
Ошибка первого рода состоит в том, что отвергается верная гипотеза.
Ошибка второго рода состоит в том, что принимается неверная гипотеза.
Вероятности и той, и другой ошибки зависят от значения , которое, в свою очередь, определяется вероятностью 
, с которой принимается решение. С повышением этой вероятности увеличивается значение (доверительный интервал), и, следовательно, вероятность ошибки первого рода уменьшается, а ошибки второго рода - возрастает, и наоборот. Таким образом, нецелесообразно принимать решение с очень высокой степенью вероятности. Обычно выбирается Р = 0,9...0,95.
3.2.4. Определение ширины доверительного интервала
для измеряемой величины
Окончательный результат представляется в форме доверительного интервала:
(15)
Значение относительного доверительного интервала для среднего значения выбирается по заданной доверительной вероятности; при этом, если подтверждена гипотеза о нормальности распределения результатов наблюдений, то распределение среднего арифметического для ряда подобных совокупностей равноточных результатов также следует считать нормальным. В этом случае значение «t» выбирается из таблиц функции Лапласа. Если же согласно априорной информации закон распределения вероятности для среднего считается неизвестным, то для увязки доверительного интервала с доверительной вероятностью используют неравенство П.Л.Чебышева:
(16)
Задавшись доверительной вероятностью Р, из выражения (16) можно определить относительную ширину t доверительного интервала.
Рассмотрим в качестве примера обработку результатов многократных измерений электрического напряжения.
Пример обработки результатов многократных измерений.
В табл.1 приведены 100 независимых числовых значений результата измерения напряжения «U»цифровым вольтметром, каждое из которых повторилось m раз. Проверить гипотезу о нормальности распределения вероятности результатов измерения. Записать результат в принятой форме, исходя из уровня доверительной вероятности 0,95. Представить два варианта доверительного интервала – для нормального и для неизвестного закона распределения вероятности среднего арифметического значения измеряемого напряжения.
Таблица 1
| U,В | 8,30 | 8,35 | 8,40 | 8,45 | 8,50 | 8,55 | 8.60 | 8,65 | 8,70 | 8,75 | 8,80 | 8,85 | 8,90 | 8,95 |
| m |
Решение
4.1. Определяем среднее арифметическое и стандартное отклонение для данных таблицы 1:
, 
4.2. С помощью правила «трех сигм» проверяем наличие или отсутствие промахов.
Таким образом, ни один из результатов не выходит за границы интервала 
, следовательно, с вероятностью 0,9973 гипотеза об отсутствии грубых погрешностей принимается.
4.3. Построение гистограммы и выдвижение гипотезы о виде закона распределения вероятности.
Для того, чтобы построить гистограмму, необходимо результаты отдельных измерений расположить в так называемый вариационный ряд по возрастанию их численных значений (в рассматриваемом примере эта процедура уже проделана и представлена таблицей 1).
Участок оси абсцисс, на котором располагается вариационный ряд значений физической величины, разбивается на k одинаковых интервалов DU. При выборе числа интервалов следует придерживаться следующих рекомендаций:
| Число измерений «n» | Число интервалов «k» |
| 40 - 100 | 7 – 9 |
| 100 - 500 | 8 – 12 |
| 500 - 1000 | 10 – 16 |
| 1000 - 10000 | 12 - 22 |
Тогда:
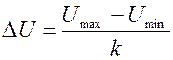
Полученное значение округляется до возможно меньшего числа значащих цифр для удобства последующих действий. В нашем случае, если принять k=11, то:
В
Начало первого интервала выбирается таким образом, чтобы это значение оказалось меньше, чем минимальный результат вариационного ряда. Последний интервал должен покрывать максимальное значение ряда. Выберем для нашего примера начало первого интервала в точке 8,275, тогда конец последнего (14-го) интервала окажется в точке 8,975.
Затем для каждого интервала подсчитывается количество результатов mi, попавших в данный интервал и определяется
Если в интервал попадает меньше пяти наблюдений, то такие интервалы объединяют с соседними, соответственно изменяется и параметр DU. Так, в нашем примере объединяются три первых и три последних интервала, их ширина становится равной 0,15 В. Общее число интервалов становится равным 10.
Результаты производимых вычислений заносятся в первую половину таблицы 2, а затем строится сама гистограмма (рис.3)
При построении гистограммы её масштаб выбирается таким образом, чтобы высота относилась к основанию примерно как 5 к 8.
Из вида гистограммы на рис.3 можно сделать предположение о том, что вероятность результата измерения подчиняется нормальному закону. Проверим правдивость этой гипотезы.
4.4. Проверка нормальности закона распределения по критерию Пирсона.
Как следует из раздела 3.2.3, для расчета критерия Пирсона необходимо знать эмпирические частоты mi/n и теоретические вероятности Рi для каждого интервала ki.
Если выдвинута гипотеза о нормальности распределения, то для расчета вероятностей используется функция Лапласа (раздел 2.1):
В данном случае значения U1 и U2 соответствуют началу и концу интервала. Для каждого из этих значений нужно рассчитать относительный доверительный интервал t (формула (8)), а затем из таблиц функции Лапласа, приведенных в приложении 1, найти соответствующие значения этой функции Ф(t1) и Ф(t2). При этом следует иметь в виду, что конец предыдущего интервала является началом последующего.
Так, например, для первого интервала:
Ф(t1) = -0,4974 Ф(t2) = -0,4463
Р1= -0,4463 - (- 0,4974) = 0,0511.
Найдя таким образом значения Рi для каждого интервала ki, заполним соответствующие ячейки таблицы 2, а затем рассчитаем значение c2 – критерия для каждого интервала и, наконец, суммарное значение c2:
c2 = 2,996
Определим табличное (критическое) значение 
, задавшись доверительной вероятностью 0,95 и вычислив по формуле r = k – 3 число степеней свободы:
r = 10 – 3 = 7
= 14,07 (приложение 2)
Таким образом, с вероятностью 0,95 гипотеза о нормальности распределения вероятности результата измерения напряжения принимается.
4.5. В тех же координатах, что и гистограмма, следует построить теоретическую кривую плотности вероятности. Для этого рассчитываются значения плотности вероятности для середины каждого интервала рi = Pi/DUi и откладываются как ординаты из середин соответствующих интервалов; полученные точки соединяют плавной кривой, симметричной относительно математического ожидания (среднего арифметического значения) (рис.3).
4.6. Представление результата в виде доверительного интервала.
Для этого определим стандартное отклонение среднего арифметического 
по формуле (12):
Как следует из раздела 3.2.4, закон распределения вероятности для среднего арифметического считаем нормальным (что следует из нормальности распределения самой измеряемой величины), тогда доверительный интервал определяется по выражению (13) при доверительной вероятности 0,95. Этому значению соответствует аргумент функции Лаплапса t = 1,96.
8,63 – 1,96×0,013 £ U £ 8,63 + 1,96×0,013
8,6 £ U £ 8,66
В случае, если закон распределения вероятности для среднего арифметического считается неизвестным, то относительный доверительный интервал рассчитывается в соответствии с неравенством Чебышева (14):
, t = 4,47
8,63 – 4,47×0,013 £ U £ 8,63 + 4,47×0,013
8,57 £ U £ 8,69
Как видно из сравнения результатов, неизвестность закона распределения вероятности приводит к расширению доверительного интервала, то есть к увеличению дефицита измерительной информации.
Таблица 2
| i | Интервалы | mi | 
| ti-1 | ti | Фi-1 | Фi | Pi |
| |
| Ui-1 | Ui | |||||||||
| 8,275 | 8,325 | 0,47 | -2,795 | -1,614 | -0,4974 | -0,4463 | 0,0511 | 0,7 | ||
| 8,325 | 8,375 | |||||||||
| 8,375 | 8,425 | |||||||||
| 8,425 | 8,475 | 1,0 | -1,614 | -1,22 | -0,4463 | -0,3888 | 0,0575 | 0,098 | ||
| 8,475 | 8,525 | 1,6 | -1,22 | -0,827 | -0,3888 | -0,2967 | 0,0921 | 0,159 | ||
| 8,525 | 8,575 | -0,827 | -0,433 | -0,2967 | -0,1664 | 0,1303 | 0,705 | |||
| 8,575 | 8,625 | 3,6 | -0,433 | -0,04 | -0,1664 | -0,016 | 0,1504 | 0,583 | ||
| 8,625 | 8,675 | 3,4 | -0,04 | 0,354 | -0,016 | 0,1368 | 0,1528 | 0,194 | ||
| 8,675 | 8,725 | 2,4 | 0,354 | 0,748 | 0,1368 | 0,2734 | 0,1366 | 0,202 | ||
| 8,725 | 8,775 | 1,8 | 0,748 | 1,142 | 0,2734 | 0,3729 | 0,0995 | 0,091 | ||
| 8,775 | 8,825 | 1,4 | 1,142 | 1,535 | 0,3729 | 0,437 | 0,0641 | 0,054 | ||
| 8,825 | 8,875 | 0,47 | 1,535 | 2,717 | 0,437 | 0,4965 | 0,0595 | 0,21 | ||
| 8,875 | 8,925 | |||||||||
| 8,925 | 8,975 |
| t | Ф(t) | t | Ф(t) | t | Ф(t) | t | Ф(t) | t | Ф(t) | t | Ф(t) | t | Ф(t) | t | Ф(t) |
| 0,00 | 0,0000 | 0,32 | 0,1255 | 0,64 | 0,2389 | 0,96 | 0,3315 | 1,28 | 0,3997 | 1,60 | 0,4452 | 1,92 | 0,4726 | 2,48 | 0,4934 |
| 0,01 | 0,0040 | 0,33 | 0,1293 | 0,65 | 0,2422 | 0,97 | 0,3340 | 1,29 | 0,4015 | 1,61 | 0,4463 | 1,93 | 0,4732 | 2,50 | 0,4938 |
| 0,02 | 0,0080 | 0,34 | 0,1331 | 0,66 | 0,2454 | 0,98 | 0,3365 | 1,30 | 0,4032 | 1,62 | 0,4474 | 1,94 | 0,4738 | 2,52 | 0,4941 |
| 0,03 | 0,0120 | 0,35 | 0,1368 | 0,67 | 0,2486 | 0,99 | 0,3389 | 1,31 | 0,4049 | 1,63 | 0,4484 | 1,95 | 0,4744 | 2,54 | 0,4945 |
| 0,04 | 0,0160 | 0,36 | 0,1406 | 0,68 | 0,2517 | 1,0 | 0,3413 | 1,32 | 0,4066 | 1,64 | 0,4495 | 1,96 | 0,4750 | 2,56 | 0,4948 |
| 0,05 | 0,0199 | 0,37 | 0,1443 | 0,69 | 0,2549 | 1,01 | 0,3438 | 1,33 | 0,4082 | 1,65 | 0,4505 | 1,97 | 0,4756 | 2,58 | 0,4951 |
| 0,06 | 0,0239 | 0,38 | 0,1480 | 0,70 | 0,2580 | 1,02 | 0,3461 | 1,34 | 0,4099 | 1,66 | 0,4515 | 1,98 | 0,4761 | 2,60 | 0,4953 |
| 0,07 | 0,0279 | 0,39 | 0,1517 | 0,71 | 0,2611 | 1,03 | 0,3485 | 1,35 | 0,4115 | 1,67 | 0,4525 | 1,99 | 0,4767 | 2,62 | 0,4956 |
| 0,08 | 0,0319 | 0,40 | 0,1554 | 0,72 | 0,2642 | 1,04 | 0,3508 | 1,36 | 0,4131 | 1,68 | 0,4535 | 2,00 | 0,4772 | 2,64 | 0,4959 |
| 0,09 | 0,0359 | 0,41 | 0,1591 | 0,73 | 0,2673 | 1,05 | 0,3531 | 1,37 | 0,4147 | 1,69 | 0,4545 | 2,02 | 0,4783 | 2,66 | 0,4961 |
| 0,10 | 0,0398 | 0,42 | 0,1628 | 0,74 | 0,2703 | 1,06 | 0,3554 | 1,38 | 0,4162 | 1,70 | 0,4554 | 2,04 | 0,4793 | 2,68 | 0,4963 |
| 0,11 | 0,0438 | 0,43 | 0,1664 | 0,75 | 0,2734 | 1,07 | 0,3577 | 1,39 | 0,4177 | 1,71 | 0,4564 | 2,06 | 0,4803 | 2,70 | 0,4965 |
| 0,12 | 0,0478 | 0,44 | 0,1700 | 0,76 | 0,2764 | 1,08 | 0,3599 | 1,40 | 0,4192 | 1,72 | 0,4573 | 2,08 | 0,4812 | 2,72 | 0,4967 |
| 0,13 | 0,0517 | 0,45 | 0,1736 | 0,77 | 0,2794 | 1,09 | 0,3621 | 1,41 | 0,4207 | 1,73 | 0,4582 | 2,10 | 0,4821 | 2,74 | 0,4969 |
| 0,14 | 0,0557 | 0,46 | 0,1772 | 0,78 | 0,2823 | 1,10 | 0,3641 | 1,42 | 0,4222 | 1,74 | 0,4591 | 2,12 | 0,4830 | 2,76 | 0,4971 |
| 0,15 | 0,0596 | 0,47 | 0,1808 | 0,79 | 0,2852 | 1,11 | 0,3665 | 1,43 | 0,4236 | 1,75 | 0,4599 | 2,14 | 0,4838 | 2,78 | 0,4973 |
| 0,16 | 0,0636 | 0,48 | 0,1844 | 0,80 | 0,2881 | 1,12 | 0,3686 | 1,44 | 0,4251 | 1,76 | 0,4608 | 2,16 | 0,4846 | 2,80 | 0,4974 |
| 0,17 | 0,0675 | 0,49 | 0,1879 | 0,81 | 0,2910 | 1,13 | 0,3708 | 1,45 | 0,4265 | 1,77 | 0,4616 | 2,18 | 0,4854 | 2,82 | 0,4976 |
| 0,18 | 0,0714 | 0,50 | 0,1915 | 0,82 | 0,2939 | 1,14 | 0,3729 | 1,46 | 0,4279 | 1,78 | 0,4625 | 2,20 | 0,4861 | 2,84 | 0,4977 |
| 0,19 | 0,0753 | 0,51 | 0,1950 | 0,83 | 0,2967 | 1,15 | 0,3749 | 1,47 | 0,4292 | 1,79 | 0,4633 | 2,22 | 0,4868 | 2,86 | 0,4979 |
| 0,20 | 0,0793 | 0,52 | 0,1985 | 0,84 | 0,2995 | 1,16 | 0,3770 | 1,48 | 0,4306 | 1,80 | 0,4641 | 2,24 | 0,4875 | 2,88 | 0,4980 |
| 0,21 | 0,0832 | 0,53 | 0,2019 | 0,85 | 0,3023 | 1,17 | 0,3790 | 1,49 | 0,4319 | 1,81 | 0,4649 | 2,26 | 0,4881 | 2,90 | 0,4981 |
| 0,22 | 0,0871 | 0,54 | 0,2054 | 0,86 | 0,3051 | 1,18 | 0,3810 | 1,50 | 0,4332 | 1,82 | 0,4656 | 2,28 | 0,4887 | 2,92 | 0,4982 |
| 0,23 | 0,0910 | 0,55 | 0,2088 | 0,87 | 0,3078 | 1,19 | 0,3830 | 1,51 | 0,4345 | 1,83 | 0,4664 | 2,30 | 0,4893 | 2,94 | 0,4984 |
| 0,24 | 0,0948 | 0,56 | 0,2123 | 0,88 | 0,3106 | 1,20 | 0,3849 | 1,52 | 0,4357 | 1,84 | 0,4671 | 2,32 | 0,4898 | 2,96 | 0,4985 |
| 0,25 | 0,0987 | 0,57 | 0,2157 | 0,89 | 0,3133 | 1,21 | 0,3869 | 1,53 | 0,4370 | 1,85 | 0,4678 | 2,34 | 0,4904 | 2,98 | 0,4986 |
| 0,26 | 0,1026 | 0,58 | 0,2190 | 0,90 | 0,3159 | 1,22 | 0,3883 | 1,54 | 0,4382 | 1,86 | 0,4686 | 2,36 | 0,4909 | 3,00 | 0,49865 |
| 0,27 | 0,1064 | 0,59 | 0,2224 | 0,91 | 0,3186 | 1,23 | 0,3907 | 1,55 | 0,4394 | 1,87 | 0,4693 | 2,38 | 0,4913 | 3,20 | 0,49931 |
| 0,28 | 0,1103 | 0,60 | 0,2257 | 0,92 | 0,3212 | 1,24 | 0,3925 | 1,56 | 0,4406 | 1,88 | 0,4699 | 2,40 | 0,4918 | 3,40 | 0,49966 |
| 0,29 | 0,1141 | 0,61 | 0,2291 | 0,93 | 0,3238 | 1,25 | 0,3944 | 1,57 | 0,4418 | 1,89 | 0,4706 | 2,42 | 0,4922 | 3,60 | 0,499841 |
| 0,30 | 0,1179 | 0,62 | 0,2324 | 0,94 | 0,3264 | 1,26 | 0,3962 | 1,58 | 0,4429 | 1,90 | 0,4713 | 2,44 | 0,4927 | 3,80 | 0,499928 |
| 0,31 | 0,1217 | 0,63 | 0,2357 | 0,95 | 0,3289 | 1,27 | 0,3980 | 1,59 | 0,4441 | 1,91 | 0,4719 | 2,46 | 0,4931 | 4,00 | 0,499968 |
| 4,50 | 0,499997 | ||||||||||||||
| 5,00 | 0,499998 |
Таблица значений функции Лапласа Ф(t)