Методы получения точечных оценок
Один из них – метод максимального правдоподобия.
Оценки, полученные методом максимального правдоподобия, обладают хорошими асимптотическими свойствами: при 
они становятся эффективными, несмещенными, состоятельными. Познакомимся с этим методом на примерах.
Метод максимального правдоподобия для дискретной случайной
Величины
Пусть x - дискретная случайная величина, распределенная по закону Пуассона с неизвестным параметром l, т.е.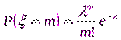 
и 
– результаты независимых наблюдений случайной величины x. Задача состоит в построении точечной оценки неизвестного параметра l. Для ее решения введем в рассмотрение функцию правдоподобия, заданную равенством 
, где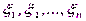 
– независимые случайные величины, распределенные так же, как и случайная величина x.
Поскольку случайные величины 
независимы и 
, то 
.
Как видно из последнего равенства, функция правдоподобия зависит только от результатов наблюдений 
и от неизвестного параметра l.
За оценку неизвестного параметра l примем такое число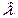 
, которое доставляет максимум функции правдоподобия.
Такой подход к построению оценки представляется естественным. В самом деле, значением функции правдоподобия является вероятность того, что случайные величины 
принимает именно те значения 
, которые увидел наблюдатель. Наблюдатель является свидетелем события, вероятность которого является наибольшей и равна 
. Такова основная идея метода максимального правдоподобия, отраженная в его названии.
При решении задач отыскания максимума функции правдоподобия чаще всего находят максимум функции lnL:
,
которая достигает максимума в той же точке, что и функция правдоподобия .
Из необходимого условия экстремума 
имеем1 искомую оценку 
неизвестного параметра l.
Так как математическое ожидание случайной величины x, имеющей распределение Пуасона с параметром l, равно 
и что эффективной несмещенной состоятельной оценкой математического ожидания x по выборке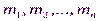 
является величина 
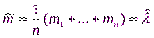, можем утверждать, что методом максимального правдоподобия получена естественная оценка параметра l.
В Mathcad для моделирования выборки случайной величины, распределенной по Пуассону, предназначена функция rpois(k,l), которая формирует вектор из k случайных чисел, распределенных по Пуассону с параметром l.
Метод максимального правдоподобия для непрерывной случайной
Величины
Пусть x - случайная величина, распределенная по показательному закону с неизвестным параметром l:
.
Задача состоит в построении методом максимального правдоподобия оценки 
параметра l по выборочным значениям 
.
По аналогии с предыдущим разделом определим функцию правдоподобия равенством
.
Как видно, функция правдоподобия зависит не только от выборочных значений, но и от неизвестного параметра распределения l. Как и выше, за оценку неизвестного параметра l примем такое число 
, которое доставляет максимум функции правдоподобия. Снова переходим к логарифму функции правдоподобия, применяем необходимое условие экстремума и после несложных вычислений получаем:
,
что естественно, поскольку математическое ожидание случайной величины, имеющей показательное распределение с параметром 
, равно 
.
В Mathcad для моделирования выборки значений случайной величины, имеющей показательное распределение, предназначена функция rexp(k,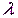 
), которая формирует вектор из k случайных чисел, распределенных показательно с параметром 
.
Задание 3.1
Метод максимального правдоподобия для дискретной случайной величины
Смоделируйте несколько выборок объема п значений случайной величины x, имеющей распределение Пуассона с параметром 
, N – номер варианта. Для одной выборки постройте график функции правдоподобия. Найдите оценку максимального правдоподобия параметра l как функцию объема выборки. Выполните вычисления для 
при 
и для 
при N >15. Изобразите на графике зависимость оценки от объема выборки. Сравните полученные оценки с заданным значением параметра.