Последовательная коррекция

РОССИЙСКАЯ ФЕДЕРАЦИЯ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ КАЛУЖСКОЙ ОБЛАСТИ

Государственное автономное профессиональное образовательное учреждение Калужской области «Калужский технический колледж»

Лабораторный практикум

 

 

Мдк 01.03. ТЕОРЕТИЧЕСКИЕ ОСНОВЫОРГАНИЗАЦИИ МОНТАЖА, РЕМОНТА, НАЛАДКИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ, СРЕДСТВ ИЗМЕРЕНИЙ И МЕХАТРОННЫХ СИСТЕМ

ПМ01. КОНТРОЛЬ И МЕТРОЛОГИЧЕСКОЕ ОБЕСПЕЧЕНИЕ СРЕДСТВ И СИСТЕМ АВТОМАТИЗАЦИИ

Основной профессиональной образовательной программы

По специальности

Автоматизация технологических процессов и производств»

Курс

 

Калуга, 2018г.

ОДОБРЕНА

Дисциплинарно-цикловой комиссией

Профессионального цикла по специальностям

Протокол №

от «___» ___________ 2018 г.

 

Председатель ___________

 

Составлена в соответствии с

требованиями ФГОС НПО/СПО по специальности (профессии)

__________________________________

___________________________________

___________________________________

 

Зам. директора по НМР

______________В.А. Никитина

 

Автор

 

Преподаватель Мелешенко М.С.

Краткая характеристика междисциплинарного курса, его цели и задачи

Место практических работ в профессиональном модуле междисциплинарного курса

 

МДК 01.03. Теоретические основы организации монтажа, ремонта, наладки систем автоматического управления, средств измерений и мехатронных систем по ПМ 01. Контроль и метрологическое обеспечение средств и систем автоматизации изучается как учебный предмет при освоении специальности СПО 15.02.07 «Автоматизация технологических процессов и производств» в объёме 60 часов, из них 50 часов лекционного материала и 10 часов практических работ.

Содержание рабочей программы дисциплины согласовано с требованиями компонента государственного стандарта среднего (полного) общего образования базового уровня.

Выполнение практических работ поможет студентам освоить обязательный минимум содержания курса, подготовиться к сдаче дифференцированного зачёта.

 

Организация и порядок выполнения практических работ

Практические работы проводятся после изучения теоретического материала. Студенты должны иметь методические рекомендации по выполнению практических работ и конспекты лекций.

 

 

1.3. Критериями оценки результатов работы студентов являются:

ü Уровень усвоения студентом учебного материала;

ü Умение студента использовать теоретические знания при выполнении практических работ;

ü Сформированность ключевых (общенаучных) компетенций;

ü Обоснованность и чёткость изложения материала;

ü Уровень оформления работы.

 

Анализ результатов

Если практическая работа выполнена в полном объёме и правильно оформлена, то ставится оценка «5».

Если практическая работа выполнена более чем на 75%, то ставится оценка «4».

Если практическая работа выполнена более чем на 60%, то ставится оценка «3».

В противном случае работа не засчитывается.

 

 

Практические работы по МДК 01.03. Теоретические основы организации монтажа, ремонта, наладки систем автоматического управления, средств измерений и мехатронных систем ПМ 01. Контроль и метрологическое обеспечение средств и систем автоматизации

Практическая работа №1

Тема: Статический режим работы системы.

 

Цель урока:

§ изучить влияние параметров структуры системы автоматического регулирования на точность в установившемся режиме;

· Развивать наблюдательность, логическое мышление, умения применять формулируемые знания в новых ситуациях;

· Воспитывать самоанализ в новых ситуациях.

Оборудование:

· Мультимедийный проектор;

· Раздаточный материал.

Студент должен знать:

· Принцип работы электродвигателя;

· Правила выбора генератора.

Студент должен уметь:

· Читать принципиальные электрические схемы;

· Рассчитывать статические характеристики системы управления;

· Строить графики статических характеристик электропривода.

Вопросы для повторения

1. Приведите классификацию по построению САР.

2. Какие признаки элементов системы управления отражаются на ее функциональной схеме?

3. Назовите наиболее распространенные функциональные элементы систем управления.

4. Как влияет коэффициент усиления системы на точность ее работы?

 

Ход работы:

1. Описание работы электропривода системы генератор-двигатель

Схема управления силовой частью системы Г-Д (рисунок 2.1) обеспечивает две рабочие скорости вращения двигателя М1: основную (номинальную) и половинную, равную 0,5. Управление системой осуществляется с помощью командо-аппарата S5, имеющего пять положений. Когда S5 находится в положении 1, двигатель М1 работает на основной характеристике, переключение в положение 2 обеспечивает вращение двигателя с половинной скоростью. В положении 3 обмотка возбуждения генератора LG1.2 отключена. В положениях 4 и 5 двигатель М1 вращается в противоположном направлении (реверс) соответственно с половинной и основной скоростью. При номинальной скорости вращения электродвигателя М1 в цепь возбуждения генератора LG1.2 включены резисторы R1 и R2, при половинной скорости – R1, R2, R3. Пуск электродвигателя осуществляется с форсировкой возбуждения генератора, выполняемой закорачиванием на время переходного процесса резисторов R2 и R3 контактами контактора К5. Отключение форсировки выполняется с помощью реле напряжения К6 и К7, включенных на шины генератора G1 и настроенных на напряжения срабатывания, соответствующие значениям выбранной скорости двигателя. Остановка электродвигателя происходит при переводе командо-аппарата в положение 3, при этом гашение энергии магнитного поля возбуждения генератора осуществляется в разрядном контуре «обмотка возбуждения LG1.2 – разрядное сопротивление R4».

Схема обеспечивает ряд защит электропривода:

от снижения тока возбуждения двигателя ниже допустимого – с помощью реле обрыва поля К9;

от превышения напряжения генератора выше допустимого – реле К8;

максимальную токовую защиту – реле К11;

нулевую защиту (от самозапуска ЭП после кратковременного исчезновения напряжения в сети переменного тока) – реле К1.

Все реле защиты воздействуют на реле нулевой защиты К1, отключающее обмотку возбуждения генератора.

 

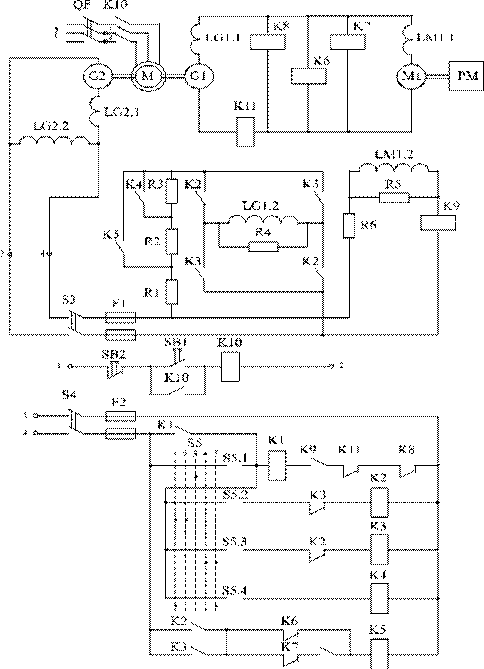
Рисунок 2.1 – Схема электрическая принципиальная системы Г-Д

2. Выбор генератора

Выбор генератора производится по номинальным данным двигателя, при этом номинальное напряжение генератора должно быть приблизительно на 5% больше напряжения двигателя, а

Iн.д. ³ Iн.г. (3.1)

где Iн.г., Iн.Д. – номинальный ток соответственно генератора и двигателя, А.

В соответствии с выше переведенными рекомендациями был выбран такой генератор:

Тип генератора П71

Номинальный ток генератора Iн.г. 69.5 А

Число витков обмотки якоря Wя.г. 297

Сопротивление якоря Rя.г. 0,224 Ом

Число витков обмотки последовательного возбуждения WО,В.г. 14

Сопротивление ОПВ Rо.вз..г 0,0115 Ом

Число витков обмотки возбуждения Wв.г. 950

Сопротивление обмотки возбуждения Rв.г. 43 Ом

Номинальное напряжение Uн.г. 230 В

Номинальная скорость nн.г. 1450 об/мин

Число пар полюсов 2р 4

Число параллельных ветвей 2а 4

Таблица 3.1- Кривая намагничивания генератора

F, A
Ф,Вб		0,0031	0,0053	0,00687	0,0081	0,0088	0,0094	0,0103

 

Рисунок 3.1 – График зависимости Фг.н.=f(Iв.г.н.)

Построим характеристику ЭДС холостого хода генератора при номинальной скорости вращения генератора . ЭДС холостого хода генератора определяем по соотношению:

, (3.2)

где Eг. –ЭДС генератора, В;

Кг. – конструктивный коэффициент генератора;

Фг. – поток возбуждения, Вб;

wг.н. – номинальная угловая скорость вращения якоря генератора, рад/с.

 

(3.3)

где n – номинальная скорость генератора, об/мин.

Конструктивный коэффициент генератора Кг определяется по формуле:

 

, (3.4)

где Wя – число витков обмотки якоря генератора;

р – число пар полюсов обмотки возбуждения генератора;

а – число параллельных ветвей обмотки якоря генератора.

Ток возбуждения генератора Iв.г, А:

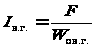, (3.5)

где F – магнитодвижущая сила, А;

Wов.г. – число витков обмотки возбуждения генератора.

Результаты расчетов для построения зависимости свести в табл. 3.2

Таблица 3.2– Расчет характеристики холостого хода генератора

Iв.г.,A	1,052	1,95	2,105	3,157	4,21	4,68	5,263	6,315	8,421	12,631
Eг., A		144,79	151,16	197,23	232,54	242,72	252,64	269,87	295,71	321,54

 

Рисунок 3.2 – Характеристика ЭДС холостого хода генератора

 

3. Расчет и построение статических характеристик электропривода.

f(М)) рассчитываются по известным соотношениям для двигателя постоянного тока независимого возбуждения:=wf(IЯ) и механическая =wСтатические характеристик (электромеханическая)

 

(4.1)

(4.2)

 

где КД. – конструктивный коэффициент двигателя;

ФН..Д. – номинальный поток его возбуждения, Вб;

- суммарное сопротивление якорной цепи, Оm.

Суммарное сопротивление якорной цепи RяS определяется суммой всех сопротивлений элементов силовой цепи, включенных последовательно с якорем генератора:

= КТ·(RЯД + RДПД+ RЯГ+ RПР+ RДПГ) + 4RЩ, (4.3)

=КТ·(RЯД + RДПД) + 2RЩ, (4.4)

 

где КТ – температурный коэффициент, учитывающий увеличение сопротивления при нагреве, КТ – 1,24;

RЯД, RЯГ – сопротивление якорной цепи двигателя и генератора, Оm;

RДПГ,RДПД – сопротивление дополнительных полюсов генератора и двигателя, Оm;

RЩ – сопротивление щеточных контактов, Оm;

RПР – сопротивление соединительных проводов, Оm.

(4.5)

 

где UЩ – падение напряжения в щеточных контактах,считаем неизменным 1В.

При определении Rпр длину соединительных проводов принять – l=25 м, провода считать медными:

 

(4.6)

 

где ρ - удельное сопротивление ОмЧмм2/м (для меди r = 0,017);

l – суммарная длина соединительных проводов, м;

j – допустимая плотность тока, j = 4 А/мм2

IН.Д. – ток якорной цепи системы Г-Д, А

; Оm;

Окончательное суммарное сопротивление якорной цепи будет иметь вид:

=1,24(0,00805+0,00655+0,00077+0,00309)+4*0,00145=0,902 Оm;

=1,24·0,28+2·0,0153=0,0129 Оm;

Произведение (КД.·ФН.Д.) определяем по паспортным данным двигателя:

 

, (4.7)

 

- номинальная угловая скорость вращения двигателя

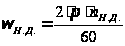
, (4.8)

,

Статический момент сопротивления находится из соотношения:

МС=КЗ· МЭМ.Н= 1·148,88 = 148,88, (4.9)

где КЗ – коэффициент нагрузки;

МЭМ.Н. – номинальный электромагнитный момент двигателя М1, Н·м.

, (4.10)

Номинальный момент на валу двигателя:

, (4.11)

где РН.Д.– номинальная мощность, Вт

Для обеспечения необходимой скорости вращения двигателя ЭДС генератора должна превышать ЭДС двигателя на величину падения напряжения в сопротивлении якорной цепи:

, SIЯ.·RЯ+Н.Д.w· ЕГ=(КД.· ФН.Д.)).124(

где IЯ. – ток двигателя, А.

Ток статической нагрузки, А:

IЯ.= IН.Д.· КЗ.=65·1=65, (4.13)

ЕГ=2,43·80,6+65·0,724=242,723 В,

Для построения статических характеристик двигателя необходимо знать всего две точки, так как они представляют собой прямую линию. В качестве таких точек удобно принять точки:

Точка идеального холостого тока (М=0, Iя=0),

Н.Д.w=wТочка, в которой М=МС со скоростью вращения

Н.Д.w=wТочка, в которой Iя.= IН.Д. со скоростью вращения

 

,

,

,

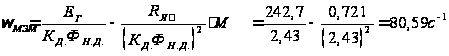Также не обходимо построить статические характеристики при ЭДС генератора работающей при половиной скорости от номинальной.

В, SIЯ.·RЯ+Н.Д/2.w· ЕГ/0,5=(КД.· ФН.Д.)).154(

ЕГ/0,5=2,43·40,3+65·0,721=144,794

,

,

,

 

Расчет естественной характеристики:

 

,

,

Рисунок 5.1- Электромеханические характеристики систем Д-Г и Д

Рисунок 5.2- Механические характеристики систем Д-Г и Д

Практическая работа №2

Тема: Динамический режим работы системы.

Цель урока:

· изучить влияние параметров структуры системы автоматического регулирования на точность в установившемся режиме;

· Развивать умения применять формулируемые знания в новых ситуациях;

· Воспитывать самоанализ в новых ситуациях.

Оборудование:

· Мультимедийный проектор;

· Раздаточный материал.

Студент должен знать:

· Принцип работы электродвигателя;

· Правила выбора генератора.

Студент должен уметь:

· Читать принципиальные электрические схемы;

· Рассчитывать динамические характеристики системы управления;

· Строить диаграммы характеристик системы управления.

Вопросы для повторения

1. Что отражает алгоритмическая схема системы управления?

2. Приведите примеры элементарных алгоритмических звеньев.

3. На какие три класса разделяются системы управления в зависимости от характера изменения задающего воздействия и управляемой величины?

Ход работы:

Динамическими называются параметры, определяющие характер протекания переходных процессов.

При расчете пренебрегают электромагнитной инерционностью якорной цепи, реакцией якорей генератора и двигателя, влиянием вихревых токов с учетом этих допущений к динамическим параметрам системы генератор-двигатель относятся:

Электромагнитная постоянная времени обмотки возбуждения генератора

 

(5.1)

 

Электромеханическая постоянная времени электропривода - ТМ

 

, (5.2)

где JД – приведенный к валу двигателя эквивалентный момент инерции всей системы ЭП, кгЧм2

JД=KJ·JД.=2·10,25=20,5, (5.3)

где KJ – коэффициент инерции привода;

JД – момент инерции якоря привода, кг·м2.

,

где LВСР – индуктивность обмотки возбуждения, Гн;

RВГ - активное сопротивление обмотки возбуждения, Оm.

Индуктивность обмотки возбуждения является переменной величиной и зависит от тока возбуждения. Пользуясь кривой намагничивания ФГ=f(F), найдем зависимость LB=f(IВ.Г.) по формуле:

 

, (5.4)

 

где ФН.Г,IВГ.Н – номинальное значение потока и тока возбуждения генератора;

н = 1,1.sн – коэффициент рассеивания магнитного потока при номиналом режиме. s

Расчеты по формуле (5.4) удобно свести в таблицу 5.1

Таблица 5.1- Расчет индуктивности обмотки возбуждения

ΔIВГ

ΔФН.Г

ΔФН.Г/ΔIВГ

(3)+(4)

(5)Ч2рWов.г.

IВСРj

 

1,052	0,0031	0,00208	0,00027	0,0023	12,22	0,526
1,053	0,0022	0,00149		0,0017	8,74	1,57
1,052	0,00157	0,00168		0,00195	6,46	2,631
1,053	0,00123	0,000647		0,00091	7,41	3,68
1,053	0,0007	0,000855		0,0011	3,45	4,73
1,052	0,0009	0,000427		0,00069	4,18	5,78
2,106	0,0009	0,000213		0,0004	2,62	7,36
4,21	0,0009	0,00294		0,0032	1,52	10,52

 

По данным таблицы 5.1 строим зависимость .

(5.5)

Рисунок 5.1-Расчет LВ.СР.

 

LВСР= 7,9 Гн,

.

 

Вывод: Управление по системе «генератор – двигатель» выгодно отличается тем, что оно не требует применения силовых контакторов, реостатов и т. п. Поскольку управление двигателем осуществляется путем регулирования сравнительно небольших токов возбуждения, оно легко поддается автоматизации. Независимое возбуждение генератора обеспечивает широкое, плавное и экономичное изменение напряжения на зажимах якоря двигателя.

Недостатками данной системы являются низкое к.п.д., большая установленная мощность из-за наличия трех машин.

 

 

Практическая работа №3

Тема: Анализ устойчивости линейных систем регулирования.

 

Цель урока:

· Научиться проводить расчёт и анализ устойчивости линейных систем регулирования;

· Развивать умения применять формулируемые знания в новых ситуациях;

· Воспитывать самоанализ в новых ситуациях.

Оборудование:

· Мультимедийный проектор;

· Раздаточный материал.

Студент должен знать:

· Критерии устойчивости САР;

· Методы синтеза САР;

· Порядок расчёта корректирующего устройства САР.

Студент должен уметь:

· Выбирать запасы устойчивости;

· Выполнять построения ЛАЧХ исходной, желаемой системы.

Вопросы для повторения

1. Какие существуют критерии устойчивости для САР?

2. Какие существуют методы синтеза САР?

3. Что такое ЛАЧХ?

4. Что можно определить по амплитуде, зная запас устойчивости?

5. Как рассчитать корректирующее устройство?

6. Для чего выполняют построения переходной характеристики замкнутой желаемой САР?

Ход работы:

Для определения устойчивости исходной замкнутой САР можно воспользоваться любым из известных критериев устойчивости, например, алгебраическим критерием Гурвица. Характеристическое уравнение замкнутой системы можно получить из передаточной функции , приравняв нулю её знаменатель

Коэффициенты этого характеристического уравнения в стандартных для критерия Гурвица обозначениях таковы

Согласно критерию Гурвица для устойчивости системы, заданной некоторым характеристическим уравнением, необходимо и достаточно, чтобы при положительности всех коэффициентов характеристического уравнения были бы положительны и все главные диагональные миноры. В нашем случае все коэффициенты положительны, проверим знаки миноров.

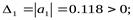
Так как минор < 0, то система в замкнутом состоянии неустойчива.

Определим граничный коэффициент усиления К_гр, при котором система находится на границе устойчивости. Для этого приравняем нулю минор и из полученного равенства найдём К_гр

Отсюда

Следовательно

<

Итак, исходная замкнутая система неустойчива, поэтому необходим синтез корректирующего устройства.

Существует много методов синтеза САР. Мы используем метод В.В.Солодовникова, базирующийся на построении логарифмических амплитудно-частотных характеристик (ЛАЧХ) исходной и желаемой систем и получения ЛАЧХ корректирующего устройства в соответствии с выражением

Построим ЛАЧХ исходной системы. Поскольку подобные характеристики строятся для разомкнутых систем, то в дальнейшем нижний индекс “р” в обозначении передаточной функции будем опускать

Этой передаточной функции соответствует амплитудно-фазовая и амплитудно-частотная частотная характеристики

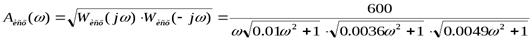
Отсюда выражение для точной ЛАЧХ запишется в виде

Сопрягающие частоты исходной ЛАЧХ находятся следующим образом

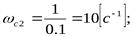
Так как передаточная функция исходной разомкнутой системы относится к III типу, то для первого участка асимптотической ЛАЧХ, т.е. для ω< ω_c1=1.43 , уравнение асимптоты ЛАЧХ будет

Это уравнение прямой линии с наклоном , проходящей при ω=1c^-1 через точку =55.563 дб.

Дальнейший ход асимптотической ЛАЧХ при увеличении частоты характеризуется тем, что на сопрягающих частотах ω_c1, ω_c2 и ω_c3 происходит изменение наклона характеристики каждый раз на (рисунок 3).

Теперь построим желаемую ЛАЧХ, т.е. ЛАЧХ устойчивой системы, отвечающей заданным требованиям к качеству регулирования.

Определим сначала частоту среза ω _{ср ж} желаемой ЛАЧХ

Из литературы известно, что при заданном перерегулировании = 30% коэффициент b в этой формуле следует выбирать равным b=3.8.

Отсюда получается

Среднечастотный (СЧ) участок проходит через частоту среза с наклоном -20 дб/дек. Известно, что низкочастотный (НЧ) участок проходит с наклоном ( 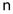-порядок астатизма, в нашем случае 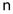=1) и если исходная система удовлетворяет требованию по точности, то НЧ участок делают совпадающим с НЧ участком L _исх(ω). Поэтому в нашем случае НЧ участки и L _исх (ω) совпадают.

Зная запас устойчивости по амплитуде можно определить протяжённость среднечастотной асимптоты при синтезе САУ. Например, для систем с астатизмом первого порядка запас устойчивости по амплитуде в отрицательной области Δ L ₂будет по модулю равен запасу устойчивости Δ L ₁ в положительной области. Δ L ₁ = |Δ L ₂|

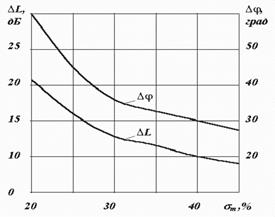
Рисунок 4 - Диаграмма Солодовникова для определения запасов устойчивости

По заданным значениям максимального перерегулирования и времени регулирования . в соответствии с номограммами предложенными Солодовниковым В.В. выбираем запасы устойчивости по модулю и по фазе.

Выбираем .

На оси ординат отметим точки с координатами , через которые проведем пунктиром горизонтальные прямые до пересечения их с линией .

Частоты, которым соответствуют точки пересечения прямых, определяют нижнюю и верхнюю границы среднечастотного диапазона (рисунок 5, это и ).

Вычислим нижнюю и верхнюю границы среднечастотного диапазона, для этого заметим, что составляет 12.8 дБ, а , тогда получаем, что:

Отметим, что , .

Среднечастотную асимптоту желаемой ЛАЧХ сопрягаем с низкочастотной и высокочастотной асимптотами.

Высокочастотный (ВЧ) участок ЛАЧХ мало влияет на динамику САР, поэтому для обеспечения простоты корректирующего устройства ВЧ участок проводят либо параллельно ВЧ участку L _исх (ω), либо совпадающим с ним.

Определим добротность желаемой системы:

Построенная, таким образом, асимптотическая представлена на рисунке 4. Передаточная функция разомкнутой скорректированной (желаемой) системы может быть, исходя из , записана следующим образом:

(1)

Желаемая замкнутая САР будет характеризоваться передаточной функцией

Прежде чем рассчитывать корректирующее устройство, определим сначала, устойчивой ли получилась скорректированная (желаемая) система и удовлетворяет ли она заданным требованиям к качеству регулирования. Поскольку уже построена , устойчивость замкнутой скорректированной системы удобнее оценить с помощью логарифмического критерия.

Базируясь на передаточную функцию разомкнутой скорректированной САР (1), найдём фазовую частотную характеристику этой системы

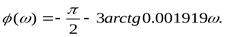
На частоте среза получим

При этом запас устойчивости по фазе будет

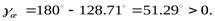
значит, желаемая САР в замкнутом состоянии устойчива.

Для проверки соответствия показателей качества регулирования спроектированной (желаемой) системы заданным требованиям построим переходную характеристику замкнутой желаемой САР Эту характеристику можно получить различными способами, мы сейчас остановимся на хорошо известном из курса ТАУ методе, опирающемся на нахождении обратного преобразования Лапласа выражения

В нашем случае

(2)

представляет собой сложное дробно-рациональное выражение, которое надо представить суммой простых дробей.

(3)

Переходная характеристика замкнутой желаемой системы найдётся, если к этому выражению применить обратное преобразование Лапласа

(4)

Теперь, задаваясь рядом фиксированных значений t_i, получим из (4) и построим график (рисунок 6), из которого найдём время регулирования и величину перерегулирования σ скорректированной системы.

Таблица 2

Рисунок 6 - График переходной характеристики скорректированной замкнутой системы

Из таблицы видно, что , т.е. время, после которого переходный процесс не выйдет из коридора , составляет приблизительно с, что удовлетворяет заданию ( с).

Максимальное значение =0.996, значит перерегулирование будет равно , что удовлетворяет заданию (σ ≤30%).

Таким образом, скорректированная система устойчива и удовлетворяет поставленным требованиям к качеству регулирования.

 

Практическая работа №4

Тема: Методы коррекции САР.

Цель урока:

§ приобретение навыков в применении метода последовательной коррекции САУ;

· Развивать умения применять формулируемые знания в новых ситуациях;

· Воспитывать самоанализ в новых ситуациях.

Оборудование:

· Мультимедийный проектор;

· Раздаточный материал.

Студент должен знать:

· Методы коррекции САР;

· Порядок построения структурной схемы САР.

Студент должен уметь:

· Создавать САР;

· Исследовать, оптимизировать и оценивать качество созданной САР;

· Корректировать САР.

Вопросы для повторения

1. Как определяются границы устойчивости САУ по корням характеристического уравнения?

2. Как записать характеристическое уравнение САУ, заданной передаточной функцией?

3. Как записать характеристическое уравнение САУ, описанной в пространстве состояний?

4. Как определяются границы устойчивости САУ по коэффициентам характеристического уравнения?

5. Как определяются границы устойчивости САУ по годографу Михайлова?

6. Как определяются границы устойчивости САУ по годографу Найквиста?

7. Дать физическую трактовку коррекции САУ с помощью пропорционально-интегрирующего и пропорционально-дифференцирующих звеньев.

Ход работы:

Коррекция САР

Обеспечение устойчивой и качественной работы САР с помо­щью дополнительных устройств называется коррекцией, а сами устройства — корректирующими элементами. Если коррекция применяется для того, чтобы сделать неустойчивую систему ус­тойчивой, то такую коррекцию часто называют стабилизацией.

Существуют различные методы коррекции САР. Наиболее час­то применяется последовательная коррекция и коррекция введе­нием дополнительных внутренних обратных связей, называемая также параллельной коррекцией.

При последовательной коррекции корректирующий элемент включают последовательно в цепь прохождения основного сигна­ла. Внутренней обратной связью охватывают одно или несколько звеньев. Если в цепи внутренней обратной связи имеется только безынерционный элемент, то ее называют жесткой обратной свя­зью. Если цепь внутренней обратной связи образована дифферен­цирующим элементом, то ее называют гибкой обратной связью.

Последовательная коррекция

Наиболее просто последовательная коррекция осуществляется введением в систему стабилизирующего звена с частотой функ­цией вида (8.20)

 

 

Где Kp=KiK2KsKiKc - коэффициент усиления разомкнутой системы.

Эквивалентную постоянную времени стабилизирующего звена выбираем равной постоянной времени самого инерционного звена,.

Сравнивая формулы (8.60) и (8.62), видно, что характер систе­мы не изменился, но постоянная времени самого инерционного звена уменьшилась с т4 до тс. Уменьшение Др за счет ввода стабилизирующего звена легко может быть скомпенсировано увеличе­нием коэффициента усиления Ki усилителя. Из-за уменьшения са­мой большой постоянной времени повышается качество процесса регулирования и запас устойчивости. Можно Kv увеличить до та­кого значения, при котором запас устойчивости остался бы преж­ним, тогда точность системы будет выше.

При наличии стабилизирующего звена управляющий сигнал будет пропорционален не только сигналу ошибки, но и его первой производной [см. формулу (8.19)]. В этом случае говорят, что кор­рекция осуществлена введением производной в сигнал управле­ния.

Жесткая обратная связь

Предположим, что жесткой обратной связью охвачен инерцион­ный элемент системы, частотная функция которого

Уменьшая Кэ легко может быть скомпенсировано увеличением коэффициента усиления усилителя системы.

Из сравнения формул следует, что жесткая обратная связь уменьшает постоянную времени инер