МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«УЛЬЯНОВСКИЙ ИНСТИТУТ ГРАЖДАНСКОЙ АВИАЦИИ
ИМЕНИ ГЛАВНОГО МАРШАЛА АВИАЦИИ Б.П. БУГАЕВА»
Факультет:Летной эксплуатации и управления воздушным движением
(ЛЭиУВД)
Кафедра:Управления воздушным движением и навигации (УВДиН)
КУРСОВАЯ РАБОТА
по учебной дисциплине«Теория УВД»
Тема: «Оптимизация потока в транспортной сети»
Вариант 3
Выполнил: курсант уч. группы Д-16-2
Пузанов И.С.
Проверил: кандидат педагогических наук,
доценткафедры УВД и Н
Карнаухов В.А.
Ульяновск, 2018
Содержание
Введение 3
Схема решения научно-производственных задач 7
Организация маршрутов движения ВС в транспортной сети (пути) 8
Моделирование и расчетная часть 9
Заключение 28
Список литературы 36
Введение
Система ОрВД является сложной многокритериальной полиэргатической системой жизнеобеспечения и управления динамическими объектами, главная цель которой – эффективное использование воздушного пространства, т.е. достижение наиболее высокой пропускной способности в условиях обеспечения безопасности, экономичности и регулярности полетов.
Эффективность функционирования системы ОрВД зависит, главным образом, от работы ее отдельных элементов, которые представляют собой этапы функционирования, определяемые, в свою очередь, отдельными процессами в этой системе. Оценка эффективности данных процессов может быть проведена с помощью показателей эффективности и количественных характеристик системы, от которых напрямую зависят ее основные критерии эффективности: безопасность, экономичность и регулярность полетов.
Данные критерии противоречивы: повышение экономичности полетов путем, например, снижения расходов на авиатопливо может негативно сказаться на их безопасности. Поэтому для наиболее эффективного функционирования системы ОрВД критерии ее эффективности должны быть связаны синергетически.
Чтобы система отвечала всем требованиям, необходимо проводить постоянный мониторинг и анализировать показатели функционирования системы за последние пять лет. При их падении необходимо выявить факторы, снижающие эффективность, и обосновать их рисками, наличие которых приводит к нарушениям, учащению нештатных ситуаций и увеличению вероятности катастроф.
Для решения проблем эффективного использования воздушного пространства, обслуживания воздушного движения и создания оптимальных условий функционирования системы в условиях многокритериальности и неопределенности с целью обеспечения гарантированной безопасности полетов целесообразно применять оптимизацию процессов на всех этапах функционирования системы.
Понятие оптимизации связано с поиском или созданием чего-то наилучшего в определенном смысле, наиболее полно удовлетворяющего определенным потребностям. Оптимизировать процесс функционирования системы – значит найти и установить такие условия, при которых наиболее полно проявляется то или иное свойство системы. Поскольку при оптимизации речь идет, главным образом, о поиске решения, оптимальность которого была бы обоснована количественно, т.е. расчетами, то, как критерий, так и ограничения, должны быть такими, чтобы они могли выражаться количественно. Кроме того, должны быть известны зависимости их значений от некоторого набора параметров. Главной общей чертой задач оптимизации является наличие цели изменения процесса, выражающегося в виде показателя эффективности рассматриваемого объекта.Под критерием оптимизации можно понимать некоторый показательфункционирования системы, который выбирается главным при постановке задачи поиска наилучшего решения. В общем виде задачу оптимизации можно сформулировать так: среди допустимых значений параметров процесса найти такие, при которых критерий достигает своего наибольшего (наименьшего) значения.
Для оптимизации системы ОрВД необходимо исследовать данную систему, выделяя на этапах функционирования процессы, достаточно полно отражающие определенную сторону системы. Выбор процесса, описание его состояния и изменения состояния его количественной характеристики является основой моделирования процессов в системе ОрВД, без которого невозможна оптимизация. Под моделированием мы понимаем процесс разработки и исследования моделей, т.е. идеальных или материальных объектов, которые в некоторых условиях заменят объект-оригинал. Объектом моделирования в системе ОрВД является транспортная сеть, представляющая собой совокупность воздушных трасс – участков в воздушном пространстве, предназначенных для полётов воздушных судов, обеспеченных трассовыми аэродромами и оборудованных средствами радионавигации, контроля и управления воздушным движением.
При исследовании сложных систем в настоящее время широко используются главным образом три вида моделей: графы систем или иконографические модели, математические и физические модели. Иконографические модели используются для представления структуры систем и соответствующих или функциональных взаимосвязей. Однако для более полного исследования больше подходят физическая или математическая модели. Идеальные (нематериальные) модели в отличие от материальных не имеют реального воплощения.Для оценки подобия модели и процессов необходимо проанализировать схожесть изменений их характеристик при одинаковых условиях. В качестве таких условий рассматриваются внешние воздействия, управляющие сигналы, действующие на процесс и, соответственно, на модель и т.д.
В системе ОрВД применяется имитационное моделирование – частный случай математического моделирования, при котором система заменяется достаточно точно описывающей ее моделью, с которой проводятся эксперименты с целью получения информации об оригинале. Но в нашей курсовой работе применение имитационного моделирования невозможно, поэтому была выбрана гомоморфная иконографическая модель транспортной сети, под которой мы понимаем ориентированный граф (модель системы объектов, связанных между собой), т.е. граф с ориентированными ребрами, в котором выделяются две вершины: S – исток (источник) и t – сток, а дугам присвоен вес, означающий пропускную способность данного участка сети. Поток представляет собой совокупность ВС, следующих по сети из S в t, причем эти ВС могут быть распределены по дугам сети различным образом.
Можно сказать, что данная модель содержит элементы, соответствующие лишь крупным частям оригинала и полное поэлементное соответствие междуними отсутствует. Это указывает на то, что наша модель, полученная путем упрощения оригинала за счет уменьшения компонент выходного сигнала или более грубой оценки его изменения во времени, – лишь идеализированный вариант транспортной сети, где не учтено множество факторов, которые могут отрицательно повлиять на ее характеристики, а также на безопасность полетов, что является наиболее важным критерием для системы ОрВД в целом.
Наша модель транспортной сети разрабатывается с целью нахождения в ней оптимального пути прохождения ВС из истока (S) в сток (t).Для этого в данной работе применяется алгоритм нахождения кратчайшего пути, заключающийся в выборе на очередном шаге вершины, до которой известно кратчайшее расстояние от S, и пересчете расстояний до вершин, смежных с рассматриваемой. Кроме того, отыскивается максимальный допустимый поток нашей сети, который будет характеризоваться интенсивностью ВД – количеством ВС, фактически поступивших в зону УВД.
Задача оптимизации потока в транспортной сети будет решена в том случае, когда поток ВС будет организован таким образом, чтобы не нарушались ограничения по пропускной способности элементов системы наряду с максимальной интенсивностью потока, распределенным по наиболее выгодным с точки зрения безопасности и экономичности маршрутам.
Схема решения научно-производственных задач:
1. Объект исследования:организация потока воздушного движения;
2. Проблема:наличие ограничений и факторов по организации воздушных трасс;
3. Цель: поиск условий эффективной организации потока ВС;
4. Предмет исследования: условие организации потока ВС;
5. Гипотеза:предлагаемые условия создают предпосылки эффективной организации потока ВС.
Исходные данные
В основе исходных данных лежит матрица смежности:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Начальный поток: λ0 = 1; S = 3; t = 8
|
Модель транспортной сети – ориентированный граф, состоящий из 8 вершин.
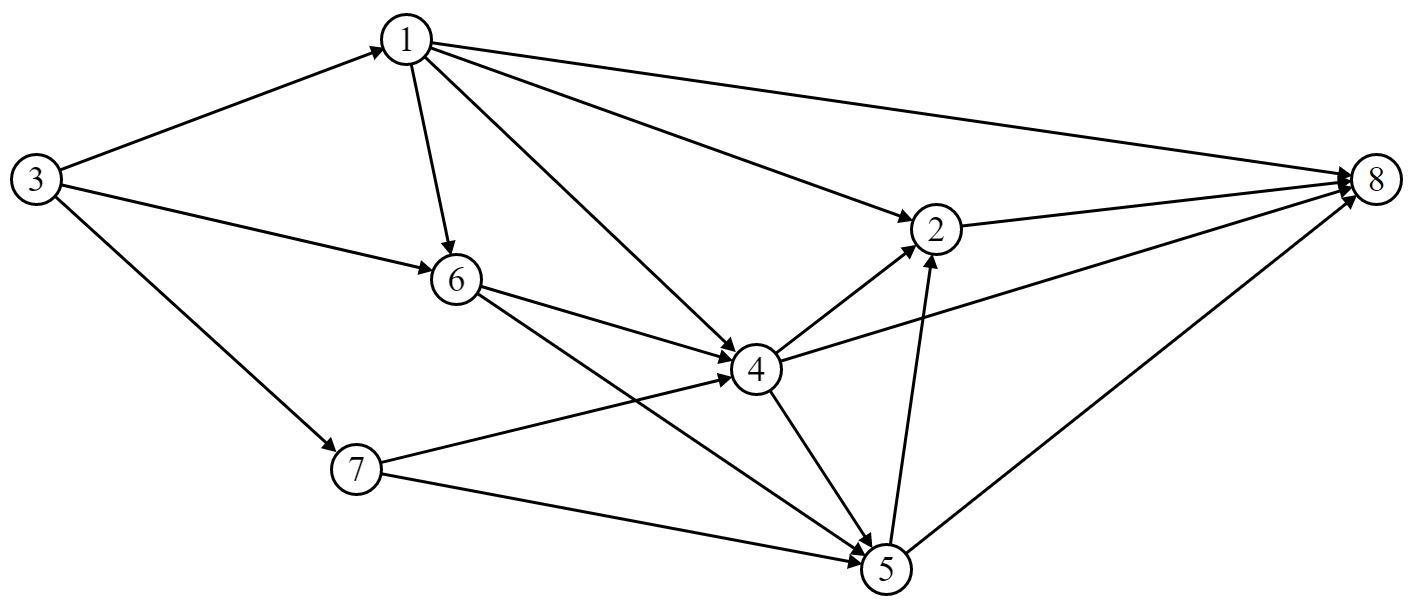
Организация маршрутов движения ВС в транспортной сети (пути):
P1 [St (3, 1, 8)]
P2 [St (3, 1, 2, 8)]
P3 [St (3, 1, 6, 4, 8)]
P4 [St (3, 1, 4, 8)]
P5 [St (3, 1, 6, 4, 2, 8)]
P6 [St (3, 1, 4, 2, 8)]
P7 [St (3, 6, 4, 8)]
P8 [St (3, 6, 5, 8)]
P9 [St (3, 1, 4, 5, 8)]
P10 [St (3, 6, 4, 2, 8)]
P11 [St (3, 6, 4, 5, 8)]
P12 [St (3, 6, 5, 2, 8)]
P13 [St (3, 7, 4, 8)]
P14 [St (3, 7, 5, 8)]
P15 [St(3, 7, 4, 2, 8)]
P16 [St (3, 7, 5, 2, 8)]
P17 [St (3, 7, 4, 5, 8)]
Моделирование и расчетная часть
Цикл 1
Шаг 1. Рассмотрим модель транспортной сети.
Выберем маршрут движения ВС (путь) P1 [St (3, 1, 8)]:
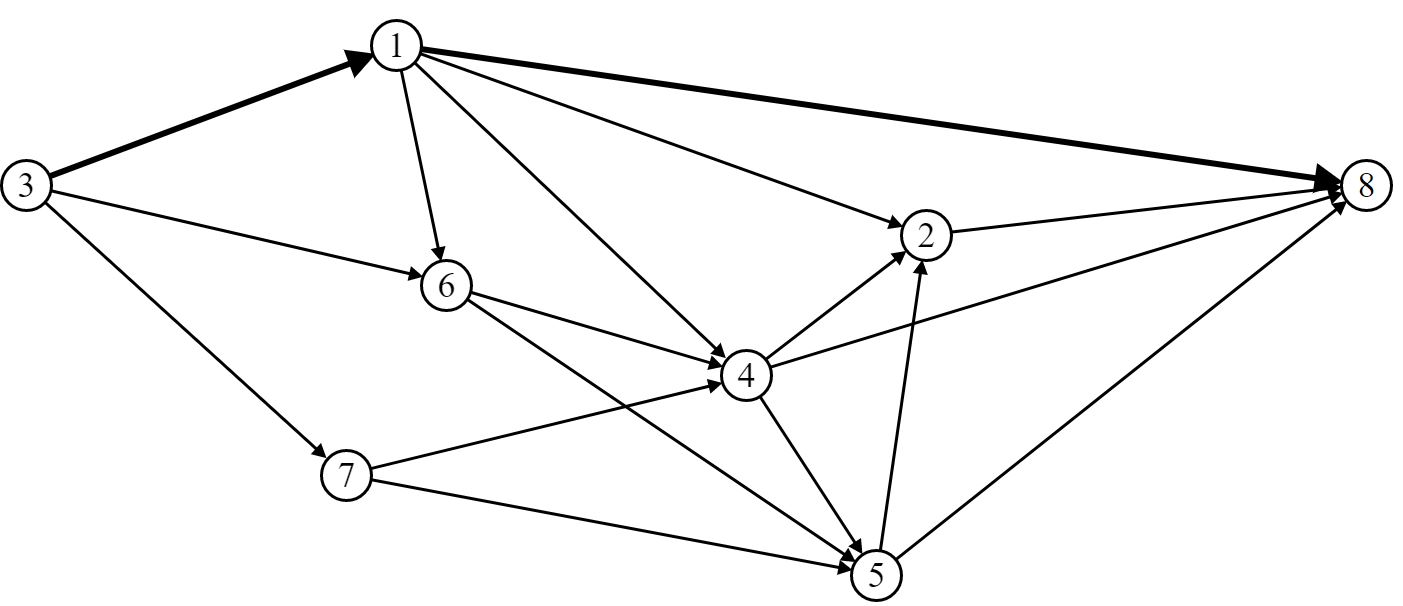
Шаг 2. Построим орграф приращения:
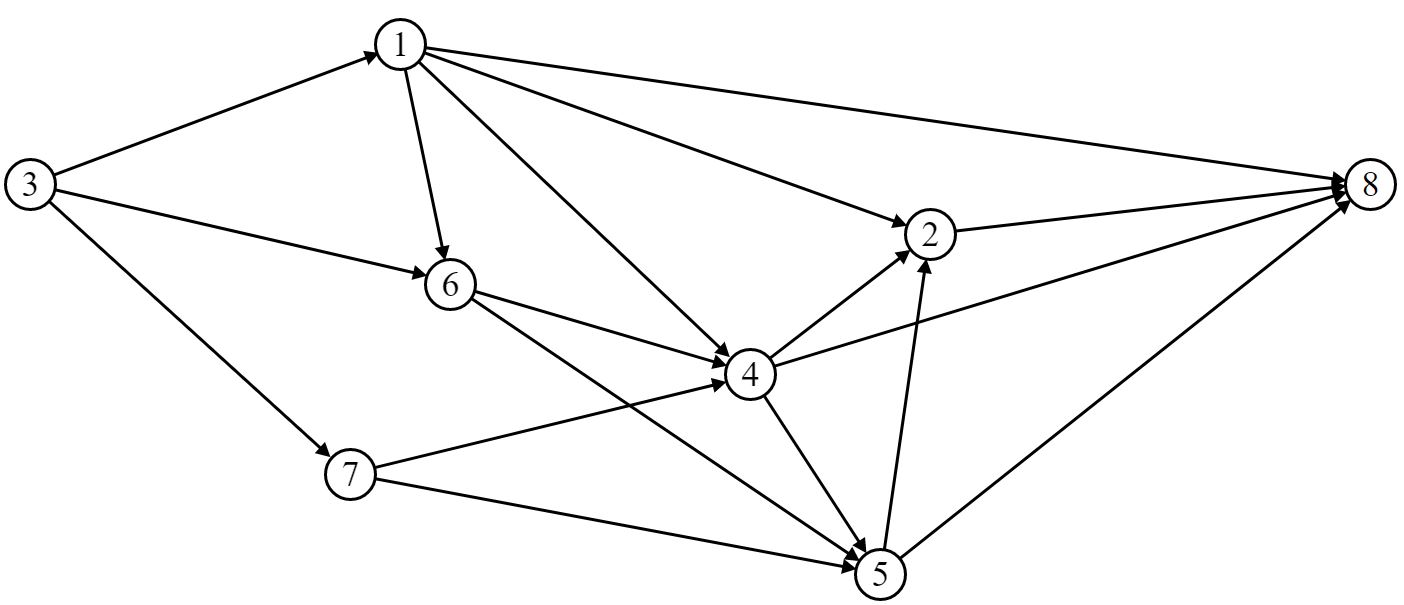
Находим путь «нулевой длины»:
3 – 1:λ< μ→ 0
1 – 8: λ<μ → 0
«Нулевой» путь найден.
| Шаг 3. Находим приращениеd:
dP1 = μminP1 – λ0
μmin P1 = (2, 2) = 2
dP1= 2 – 1 = 1
| Шаг 4. Находим новый поток:
λ1 = λ0 + dP1
λ1= 1 + 1 = 2
Цикл завершен.
|
Цикл 2
Шаг 1. Рассмотрим модель транспортной сети.
Выберем маршрут движения ВС (путь) P2 [St (3, 1, 2, 8)]:
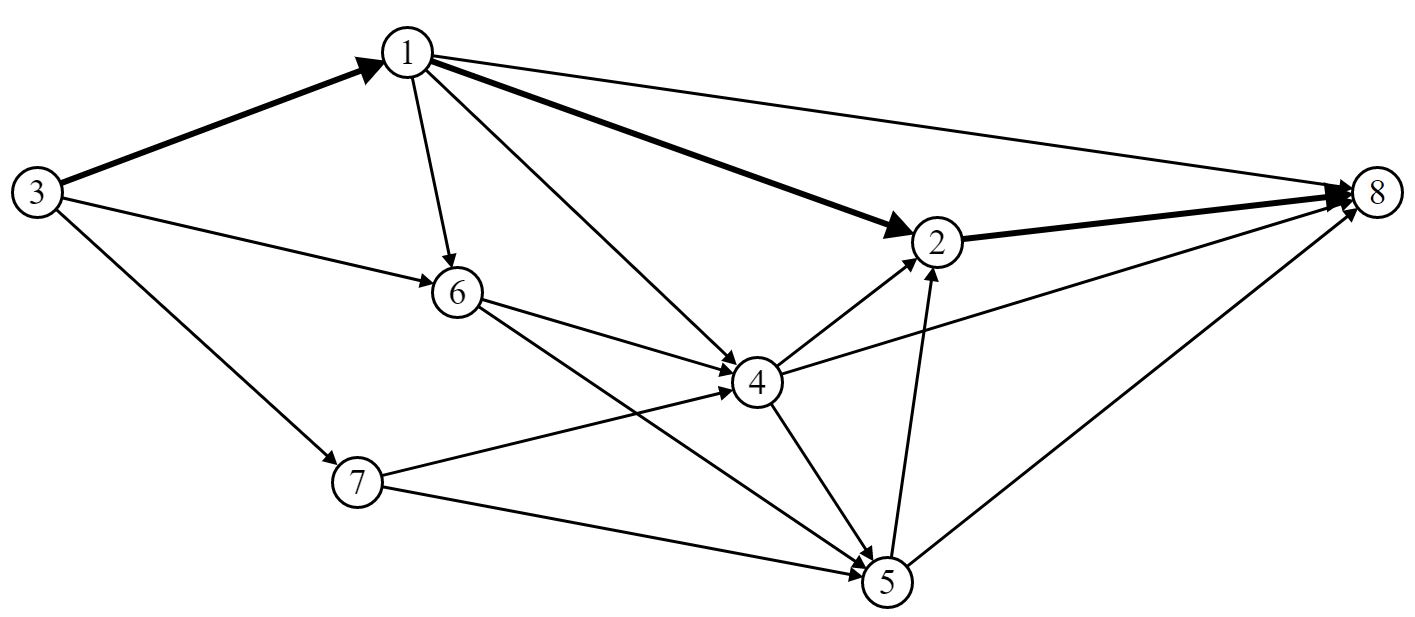
Шаг 2. Построим орграф приращения:

Находим путь «нулевой длины»:
3 – 1:λ < μ→ 0
1 – 2: λ <μ → 0
2 – 8: λ <μ → 0
«Нулевой» путь найден.
| Шаг 3. Находим приращение d:
dP2= μminP2– λ0
μminP2= (2, 2, 4) = 2
dP2= 2 – 1 = 1
| Шаг 4. Находим новый поток:
λ2= λ0 + dP2
λ2= 1 + 1 = 2
Цикл завершен.
|
Цикл3
Шаг 1. Рассмотрим модель транспортной сети.
Выберем маршрут движения ВС (путь) P3 [St (3, 1, 6, 4, 8)]:
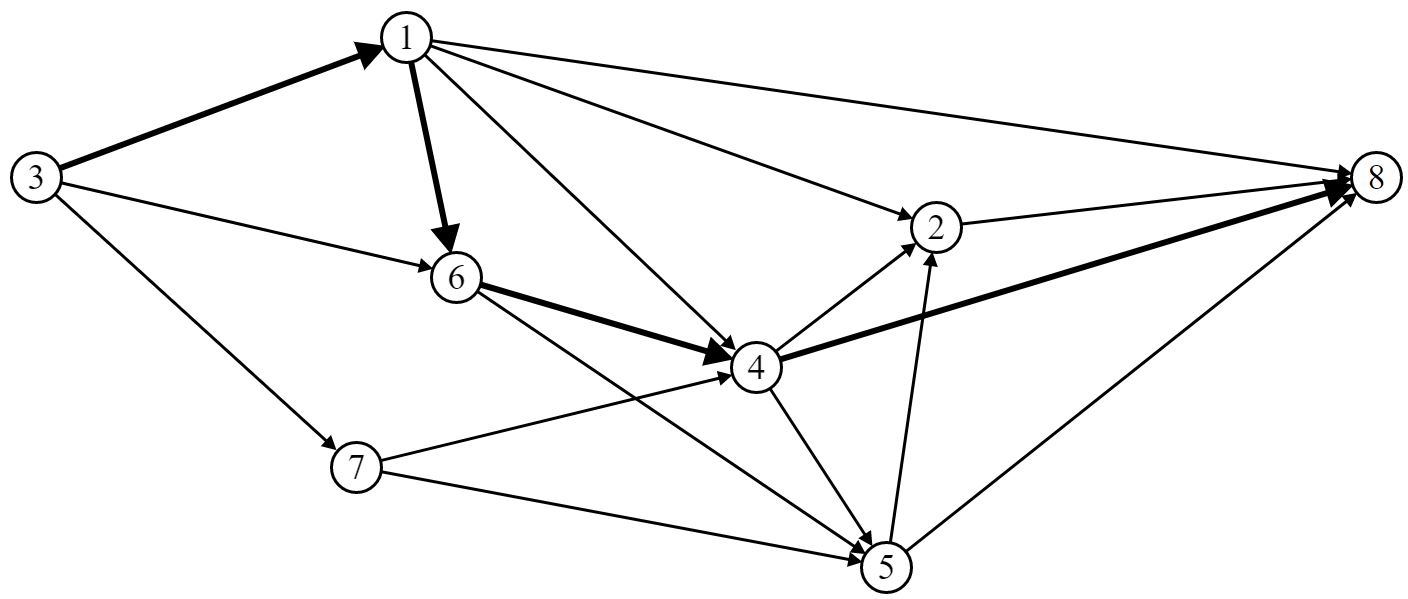
Шаг 2. Построим орграф приращения:

Находим путь «нулевой длины»:
3 – 1:λ < μ→ 0
1 – 6: λ =μ → ∞
6 – 4: λ <μ → 0
4 – 8: λ <μ → 0
«Нулевой» путьне найден.
Конец работы алгоритма.
Цикл 4
Шаг 1. Рассмотрим модель транспортной сети.
Выберем маршрут движения ВС (путь) P4 [St (3, 1, 4,8)]:
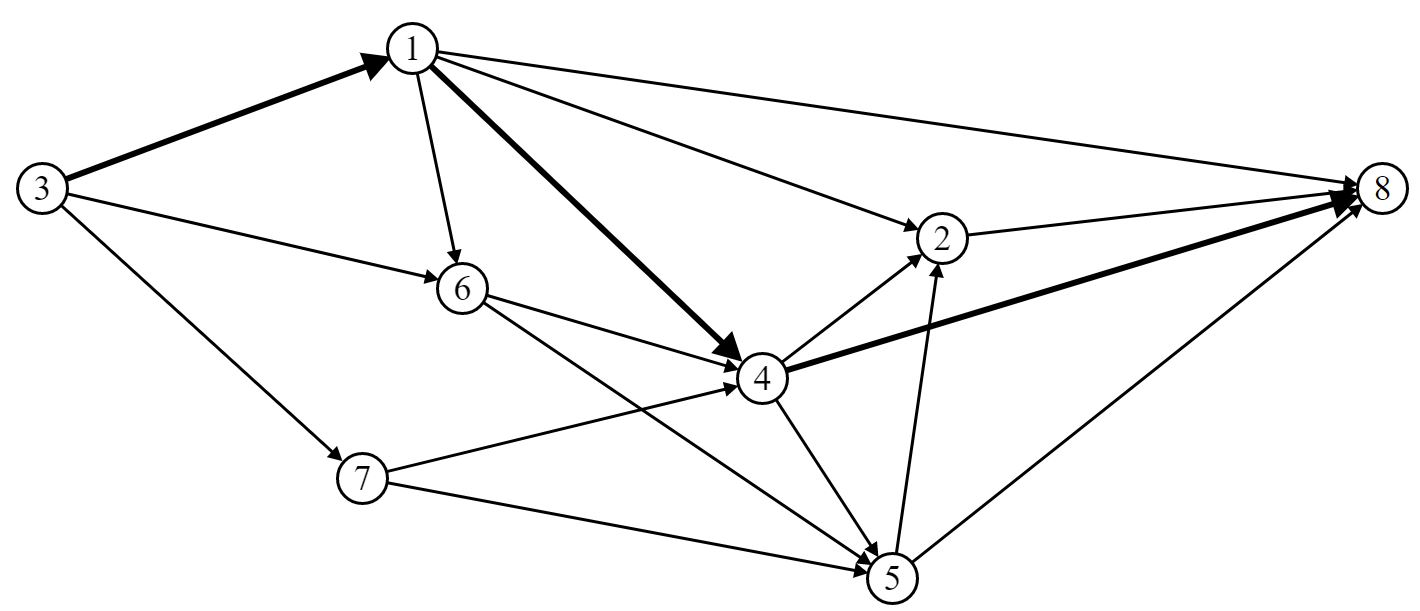
Шаг 2. Построим орграф приращения:

Находим путь «нулевой длины»:
3 – 1:λ < μ→ 0
1 – 4: λ <μ → 0
4 – 8: λ <μ → 0
«Нулевой» путьнайден.
| Шаг 3. Находим приращение d:
dP4= μminP4– λ0
μminP4= (2, 2, 5) = 2
dP4= 2 – 1 = 1
| Шаг 4. Находим новый поток:
λ3= λ0 + dP4
λ3= 1 + 1 = 2
Цикл завершен.
|
Цикл5
Шаг 1. Рассмотрим модель транспортной сети.
Выберем маршрут движения ВС (путь) P5 [St (3, 1, 6, 4, 2, 8)]:
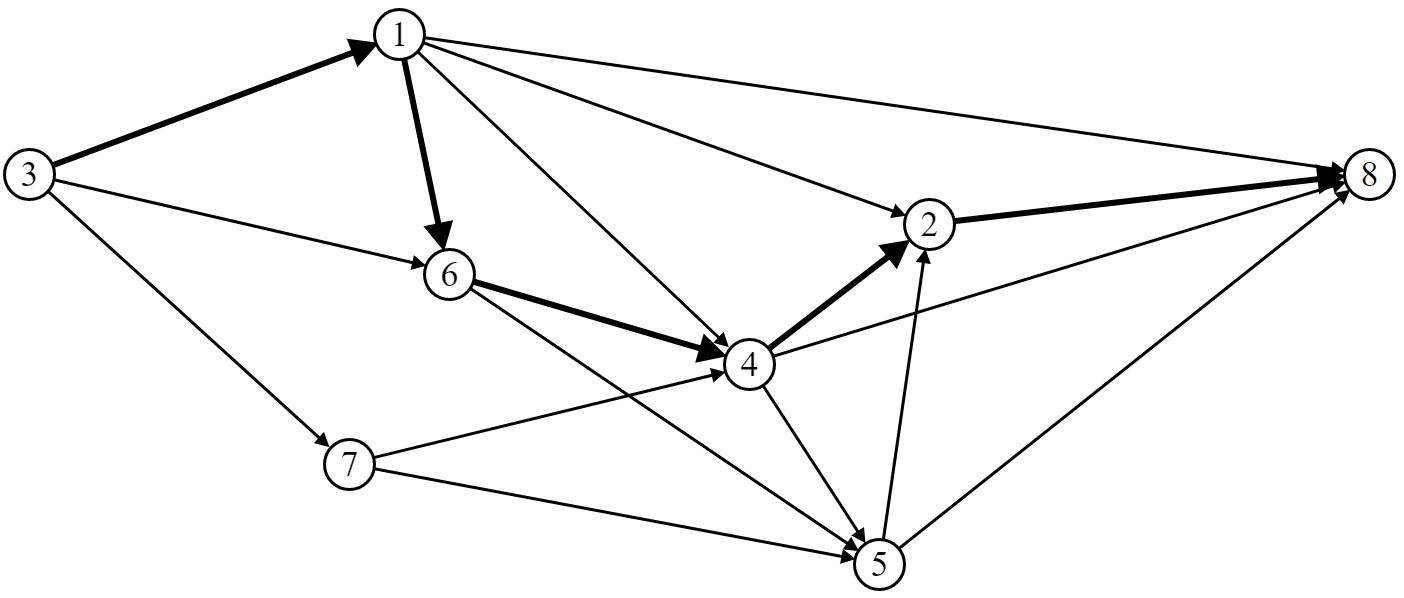
Шаг 2. Построим орграф приращения:

Находим путь «нулевой длины»:
3 – 1:λ < μ→ 0
1 – 6: λ =μ → ∞
6 – 4: λ <μ → 0
4 – 2: λ <μ → 0
2 – 8: λ <μ → 0
«Нулевой» путьне найден.
Конец работы алгоритма.
Цикл 6
Шаг 1. Рассмотрим модель транспортной сети.
Выберем маршрут движения ВС (путь) P6 [St (3, 1, 4, 2, 8)]:
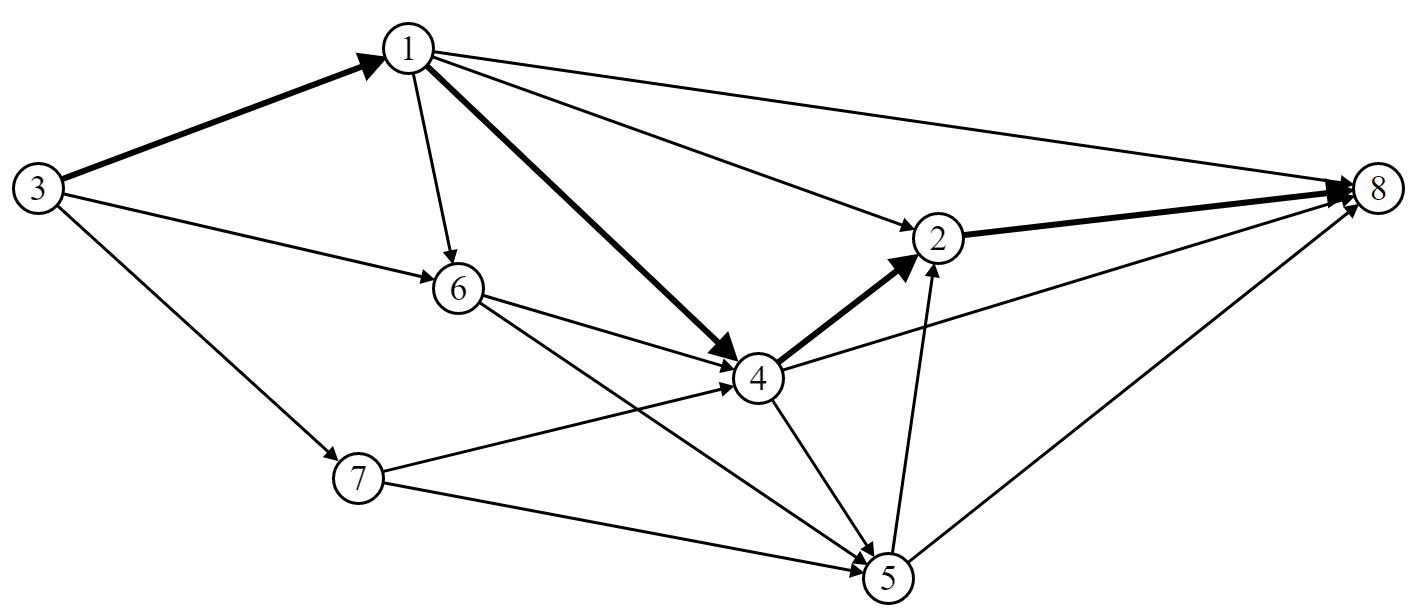
Шаг 2. Построим орграф приращения:

Находим путь «нулевой длины»:
3 – 1:λ < μ→ 0
1 – 4: λ <μ → 0
4 – 2: λ <μ → 0
2 – 8: λ <μ → 0
«Нулевой» путьнайден.
| Шаг 3. Находим приращение d:
dP6= μminP6– λ0
μminP6= (2, 2, 4, 4) = 2
dP6= 2 – 1 = 1
| Шаг 4. Находим новый поток:
λ4= λ0 + dP6
λ4= 1 + 1 = 2
Цикл завершен.
|
Цикл7
Шаг 1. Рассмотрим модель транспортной сети.
Выберем маршрут движения ВС (путь) P7 [St (3, 6, 4, 8)]:
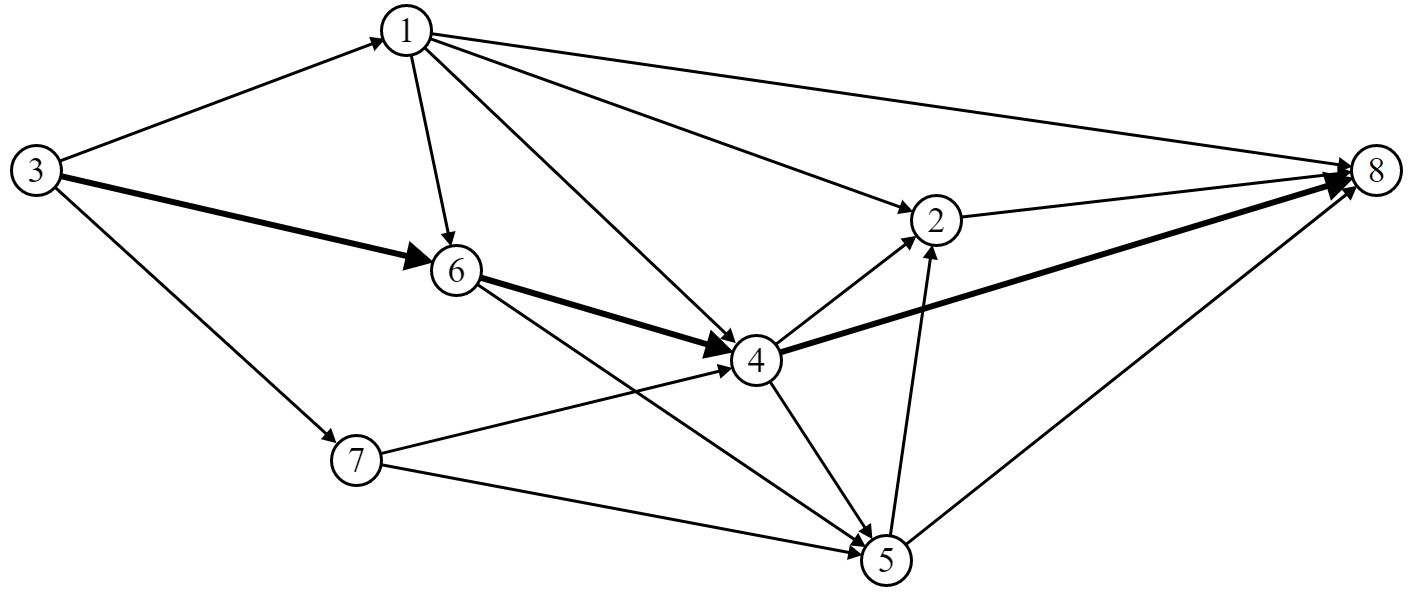
Шаг 2. Построим орграф приращения:

Находим путь «нулевой длины»:
3 – 6:λ < μ→ 0
6 – 4: λ <μ → 0
4 – 8: λ <μ → 0
«Нулевой» путь найден.
| Шаг 3. Находим приращение d:
dP8= μminP8– λ0
μminP8= (2, 3, 5) = 2
dP8= 2 – 1 = 1
| Шаг 4. Находим новый поток:
λ6= λ0 + dP8
λ6= 1 + 1 = 2
Цикл завершен.
|
Цикл 8
Шаг 1. Рассмотрим модель транспортной сети.
Выберем маршрут движения ВС (путь) P8 [St (3, 6, 5, 8)]:
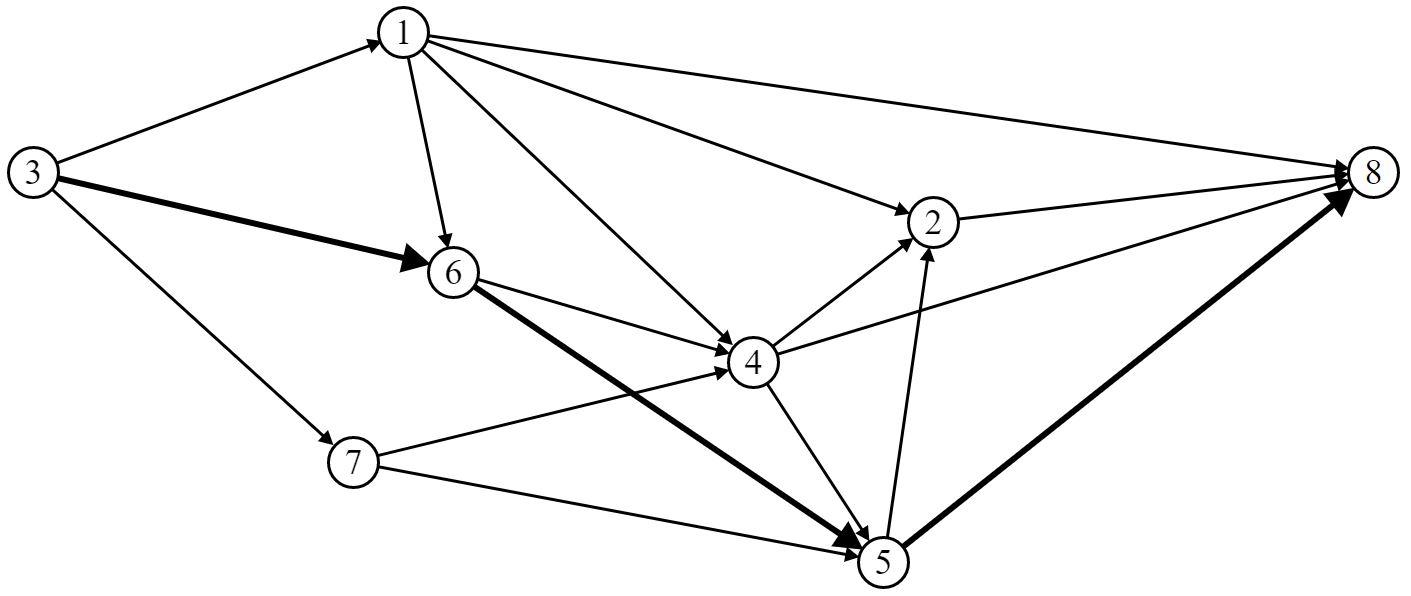
Шаг 2. Построим орграф приращения:

Находим путь «нулевой длины»:
3 – 6:λ < μ→ 0
6 – 5: λ <μ → 0
5 – 8: λ =μ → ∞
«Нулевой» путьне найден.
Конец работы алгоритма.
Цикл9
Шаг 1. Рассмотрим модель транспортной сети.
Выберем маршрут движения ВС (путь) P9 [St (3, 1, 4, 5, 8)]:
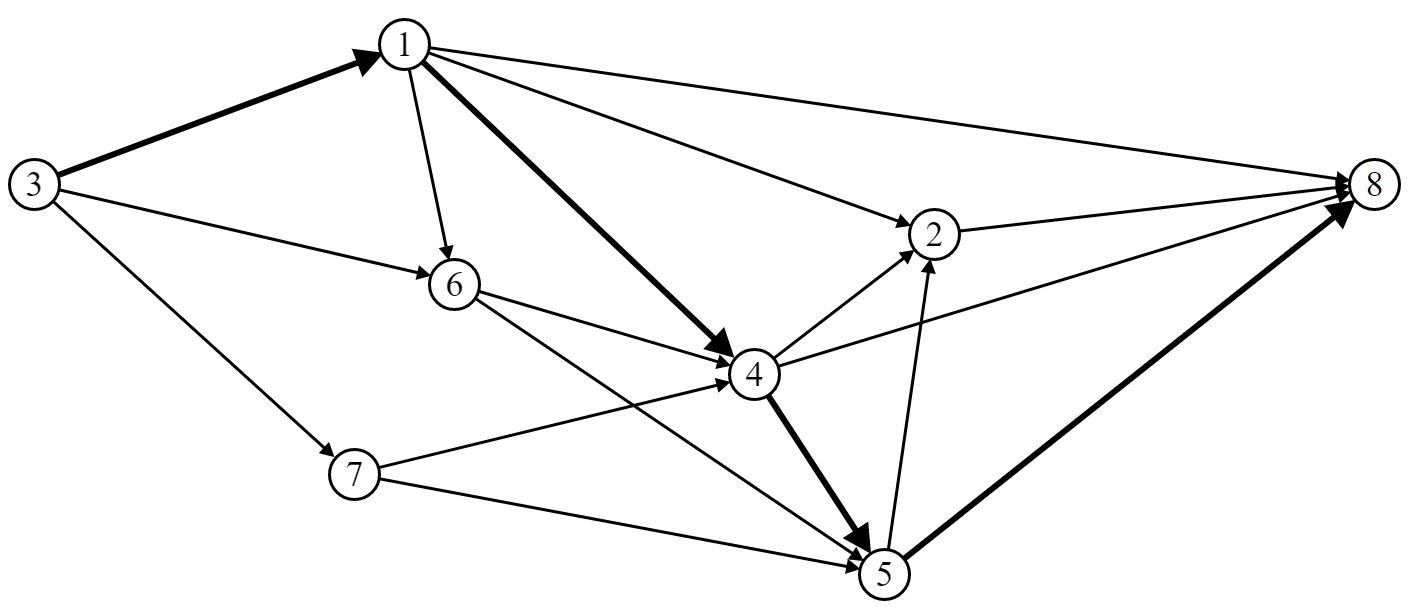
Шаг 2. Построим орграф приращения:

Находим путь «нулевой длины»:
3 – 1:λ < μ→ 0
1 – 4: λ <μ → 0
4 – 5: λ <μ → 0
5 – 8: λ =μ → ∞
«Нулевой» путьне найден.
Конец работы алгоритма.
Цикл 10
Шаг 1. Рассмотрим модель транспортной сети.
Выберем маршрут движения ВС (путь) P10 [St (3, 6, 4, 2, 8)]:
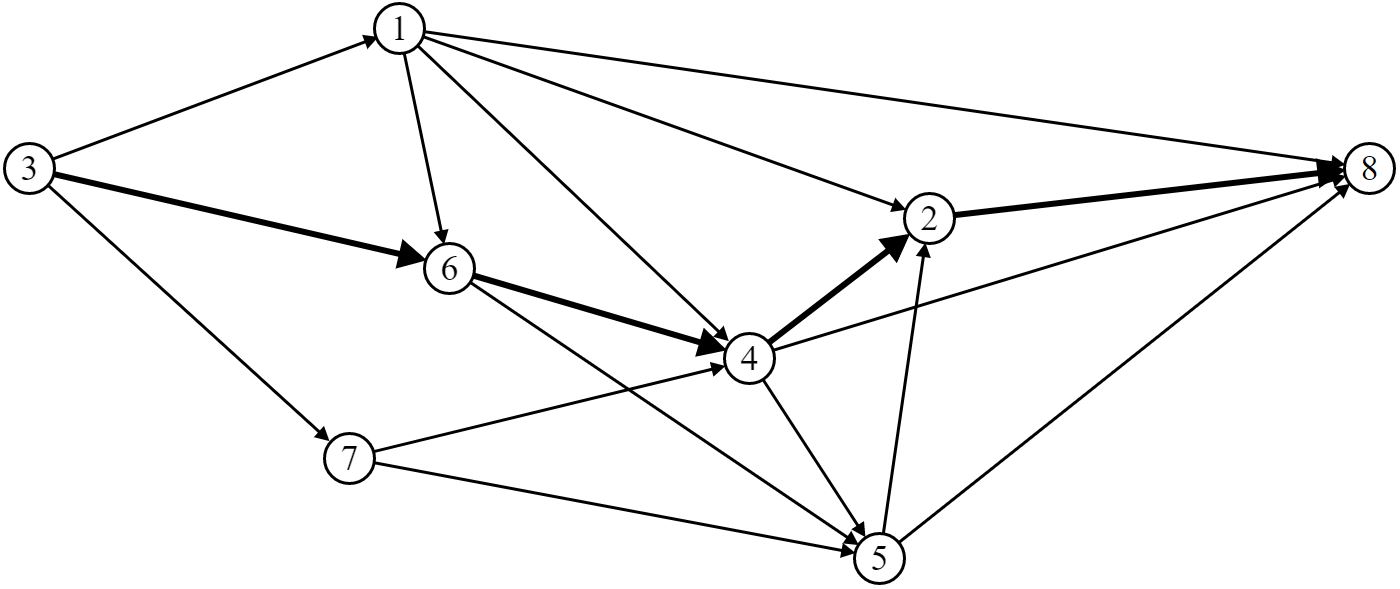
Шаг 2. Построим орграф приращения:

Находим путь «нулевой длины»:
3 – 6:λ < μ→ 0
6 – 4: λ <μ → 0
4 – 2: λ <μ → 0
2 – 8: λ <μ → 0
«Нулевой» путь найден.
| Шаг 3. Находим приращение d:
dP10= μminP10– λ0
μminP10= (2, 3, 4, 4) = 2
dP10= 2 – 1 = 1
| Шаг 4. Находим новый поток:
λ7= λ0 + dP10
λ7= 1 + 1 = 2
Цикл завершен.
|
Цикл 11
Шаг 1. Рассмотрим модель транспортной сети.
Выберем маршрут движения ВС (путь) P11 [St (3, 6, 4, 5, 8)]:
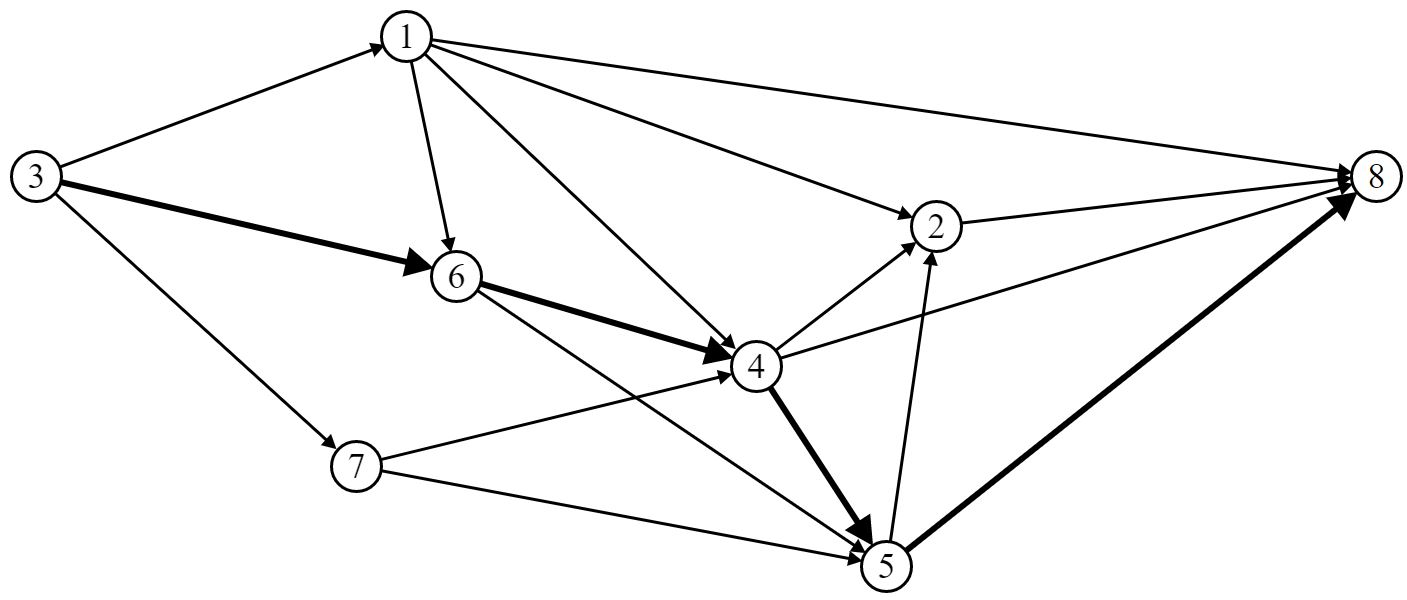
Шаг 2. Построим орграф приращения:
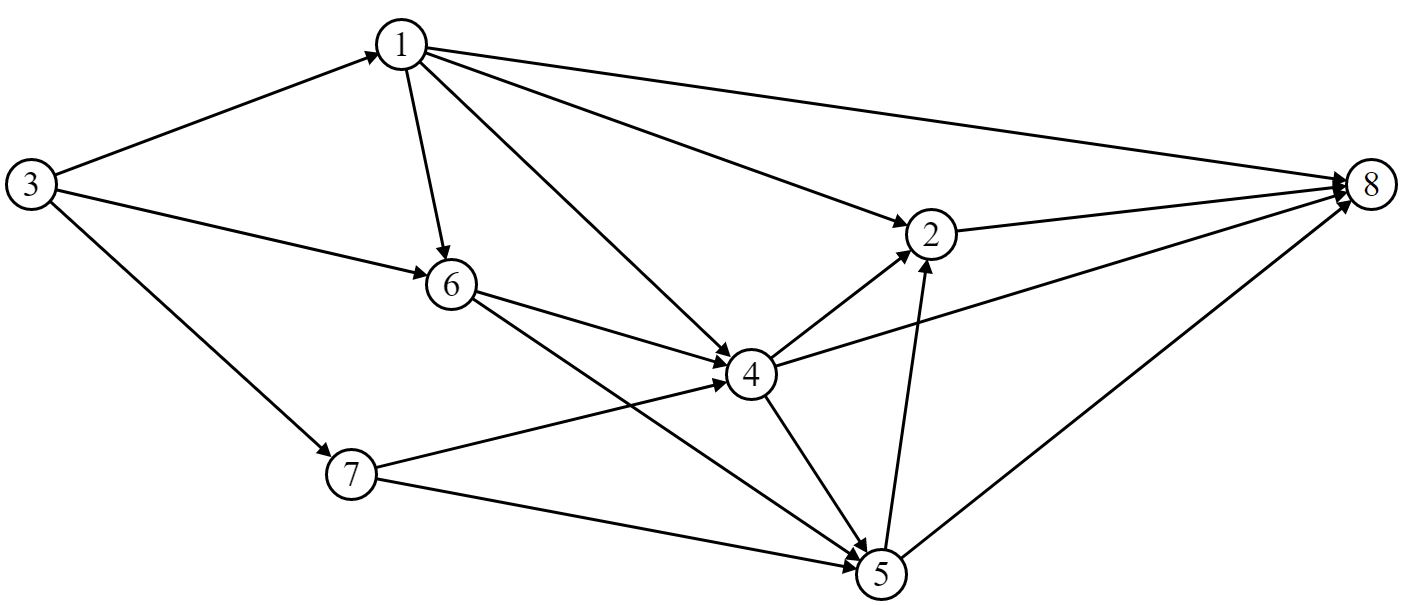
Находим путь «нулевой длины»:
3 – 6:λ < μ→ 0
6 – 4: λ <μ → 0
4 – 5: λ <μ → 0
5 – 8: λ =μ → ∞
«Нулевой» путьне найден.
Конец работы алгоритма.
Цикл 12
Шаг 1. Рассмотрим модель транспортной сети.
Выберем маршрут движения ВС (путь) P12 [St (3, 6, 5, 2, 8)]:
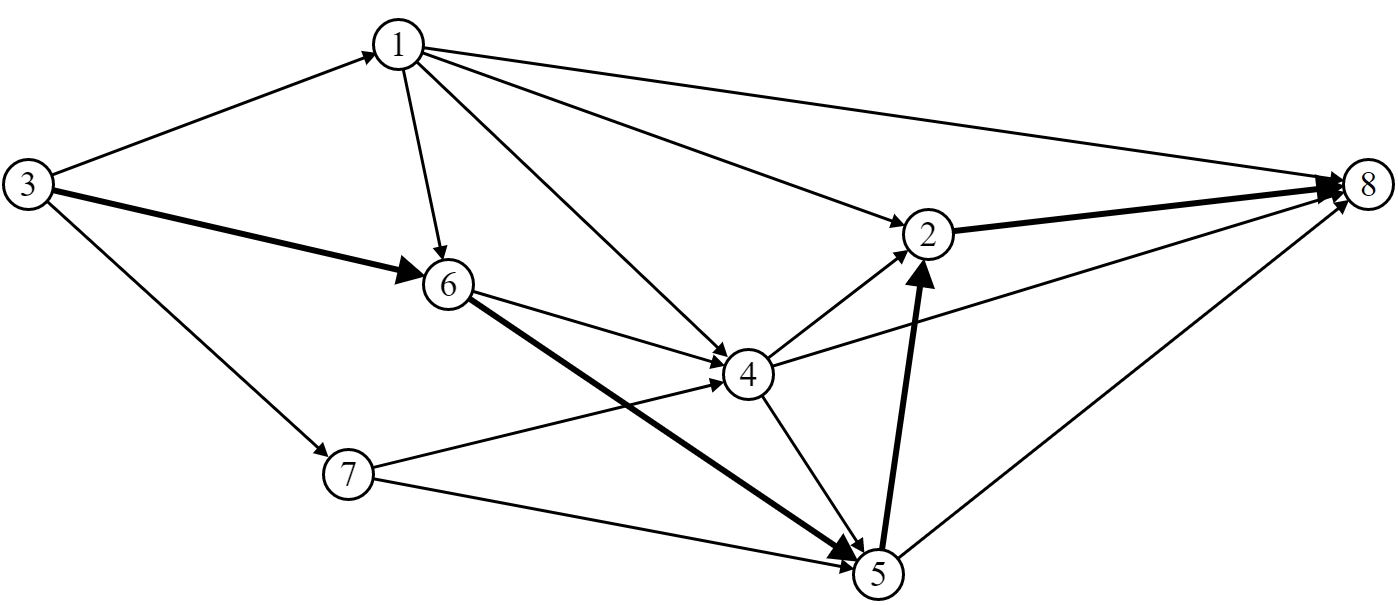
Шаг 2. Построим орграф приращения:

Находим путь «нулевой длины»:
3 – 6:λ < μ→ 0
6 – 5: λ <μ → 0
5 – 2:λ < μ→ 0
2 – 8: λ <μ → 0
«Нулевой» путь найден.
























