Математическое моделирование задачи теплопроводности стержня

Уравнение теплопроводности для линейного элемента имеет вид

, (11.1)

где - плотность материала , - теплоемкость единицы массы , – коэффициент теплопроводности , 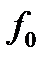– плотность тепловых источников , u – температура , - время , – лагранжева координата .

При уравнение (1.1) принимает вид

, (11.2)

где – коэффициент теплопроводности, а .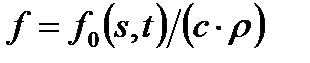

Рассмотрим (1.2) в безразмерном виде, для чего вводится следующие безразмерные параметры , , , где - длина пролета. Тогда уравнение (1.2) приобретает безразмерный вид , или, если в этом выражении опустить нижние индексы, то запишется в виде

, (11.3)

где .

10.2. Уравнение теплопроводности в разностном представлении

Уравнение (11.3) в разностном представлении по явной схеме имеет вид

,

где 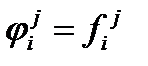, , - шаг разбиения по лагранжевой координате, – число разбиений пролета,

,

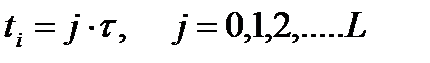где – шаг интегрирования по времени, – число разбиений временного интервала. Отсюда

. (11.4)

Устойчивость схемы в сеточной норме для шага интегрирования требует выполнения условия

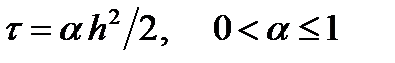. (11.5)

11.3 Аппроксимация граничных условий

Аппроксимацию граничных условий можно проводить двумя способами.

Вариант 1. Для аппроксимации граничных условий воспользуемся квадратичным полиномом Лагранжа по трем точкам отрезка.

Для первых производных по времени на концах отрезка имеем

,

.

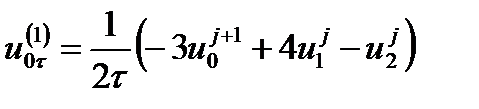Первые производные на границе аппроксимируются со вторым порядком точности (лабораторная работа №7).

А для вторых производных по координате на границе имеем

.

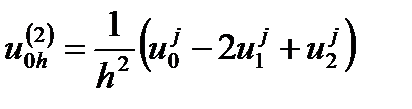
Вторые производные на границе аппроксимируются с первым порядком точности.

Тогда для границ на шаге интегрирования имеем

,

. (11.6)

Вариант 2. Для границ воспользуемся линейной аппроксимацией

,

.

Тогда имеем

,

. (11.7)

Для выбора варианта аппроксимации проводятся тестовые расчеты по обоим вариантам. Результаты тестовых расчетов приводятся ниже.

11.4 Примеры расчета теплопроводности

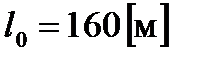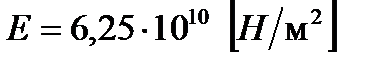Для расчетов примем следующие исходные данные: начальная длина провода ; коэффициент линейного расширения алюминиевого провода составляет [2]; модуль упругости - провода марки ЗАЛП [1]; диаметр провода ; плотность материала провода ; теплоемкость единицы массы ; коэффициент теплопроводности , – плотность тепловых источников; температура Кельвина. Количество дискретных элементов в разбиении длины провода для разностной схемы .

Задача 1. В начальном состоянии температура провода равна температуре окружающей среды (минус 5°C). Пусть теплоизолированный провод разделен на две части. Мгновенно левый пролет нагрет до 200°C (473,15 ), а правый имеет температуру окружающей среды (минус 5°C (267,15 )). В безразмерном виде эти температуры составят и 0,9817. Перераспределение температуры по длине и по времени происходит без потери тепла (теплоизолированный провод) и процесс продолжается до температуры выравнивания до теоретической (безразмерной) величины

,

что соответствует .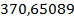

Расчеты теплопроводности проводим по подразделам (11.2-11.3) при аппроксимации граничных условий по варианту 1 и варианту 2 и сравниваем с теоретическим значением, чтобы выбрать вариант аппроксимации, с которым будут в дальнейшем проводиться расчеты.

По варианту 1 (аппроксимация граничных условий квадратичным полиномом Лагранжа) численный расчет дает температуру выравнивания или 371,64243 выравнивание температуры происходит примерно за 2,3 с.

По варианту 2 (линейная аппроксимация граничных условий) расчет дает или 370,6345 . Вариант 2 дает наилучшую сходимость с теоретическим значением.

Таким образом, в дальнейших расчетах граничные условия будем аппроксимировать по линейному закону, по варианту 2.

10.5. Линейное тепловое расширение

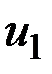Пусть - начальная длина провода при температуре и – конечная длина провода при температуре , при этом удлинение провода, а = - – разность температуры. Коэффициент линейного расширения обозначим 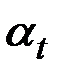. В соответствии законом линейного расширения имеем

Тогда конечная длина равна . Относительное температурное расширение составляет

(11.8)
Усилие, возникающее в проводе за счет температурного расширения составит

(11.9)

Численные расчеты по выше принятым исходным данным дают: относительное температурное удлинение составляет , усилие, возникающее в проводе за счет температурного удлинения соответственно .

Задача 2. Теперь рассмотрим следующую задачу: Пусть 1/10 часть пролета имеет температуру 200°С и со временем не изменяется. Остальная часть пролета в начальный момент имеет температуру минус 5°С, и она за счет теплопроводности нагревается.

Расчеты показывают, что температура выравнивается примерно через 4 секунды до температуры 200°С на всем пролете. И при этом температурное натяжение составляет .

Задание на проведение расчетов по № списка журнала:

1) 1/(№+1) часть пролета имеет температуру 200°С и со временем не изменяется. Остальная часть пролета в начальный момент имеет температуру минус 5°С, и она за счет теплопроводности нагревается. Определить температуру выравнивания стержня, время выравнивания температуры от начала и до конца процесса.

2) Определить температурное натяжение в конце нагрева стержня.

В приложении приводится текст программы написанный на Visual Fortran-e ориентированный на сопровождении Windous XP.

Для написании программ на других алгоритмических языках можно использовать этот алгоритм. А тестовую обработку можно провести по работе [1].

Литература

1. Гимадиев Р.Ш., Гимадиева Т.З. Математическое моделирование деформирования линии электропередачи с учетом теплопроводности // Известия высших учебных заведений. Проблемы энергетики. 2011. № 9. С. 51-59.